3.8: Flow Past a Sphere at High Reynolds Numbers
- Page ID
- 4807
So far we have considered flow past a sphere only from the standpoint of dimensional analysis, in Chapter 2, to derive a relationship between drag coefficient and Reynolds number, and we have looked at flow patterns and fluid forces only at very low Reynolds numbers, in the Stokes range. You are now equipped to deal with flow past a sphere at higher Reynolds numbers.
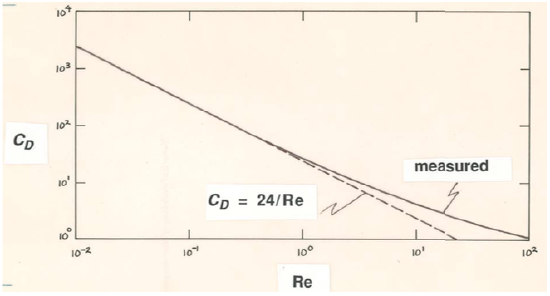
As the Reynolds number increases, flow separation gradually develops, and this corresponds to a change from a regime of flow dominated by viscous effects, with viscous forces and pressure forces about equally important, to a regime of flow dominated by flow-separation effects, with pressure forces far larger than viscous forces. This gradual change in the flow regime is manifested in the change from the descending-straight-line branch of the curve for drag coefficient \(C_{D}\) as a function of Reynolds number (see Figure 2.3.1) to the approximately horizontal part of the curve at higher Reynolds numbers. Even before separation is fully developed, there are deviations of the observed drag coefficient from that predicted by Stokes’ law (Figure \(\PageIndex{1}\)), but, after flow separation well established, the curve for \(C_{D}\) shows no relationship whatsoever to Stokes’ law (Figure 2.3.1).
In this section we will examine in a qualitative way the gradual but fundamental ways the flow pattern around the sphere changes as the Reynolds number increases. These changes can be classified or subdivided into several stages, which could well be called flow regimes. Flow regimes are distinctive or characteristic patterns of flow, which are manifested in certain definite ranges of flow conditions and which are qualitatively different from other regimes that are manifested in neighboring ranges of flow conditions. The flow regimes associated with flow around a sphere are intergradational but distinctive. Keep in mind that they are characterized or described completely by the Reynolds number, and only by the Reynolds number: it is not just the size of the sphere, or the velocity of flow around it, or the kind of fluid; it is how all of these combine to give a particular value of the Reynolds number.
Figure \(\PageIndex{2}\) shows a cartoon series of flow patterns with increasing \(\text{Re}\), and the corresponding position on the drag-coefficient curve (Figure 2.3.1). Looking ahead to the following section on settling of spheres, these figures also give approximate values of the diameters of quartz spheres settling in water at the given Reynolds numbers, and the corresponding settling velocity, in centimeters per second.
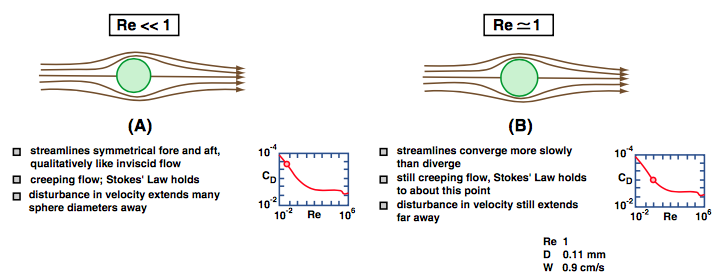
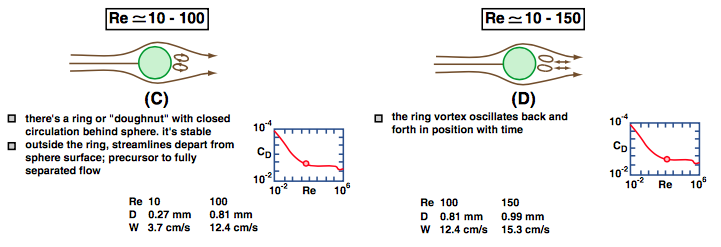
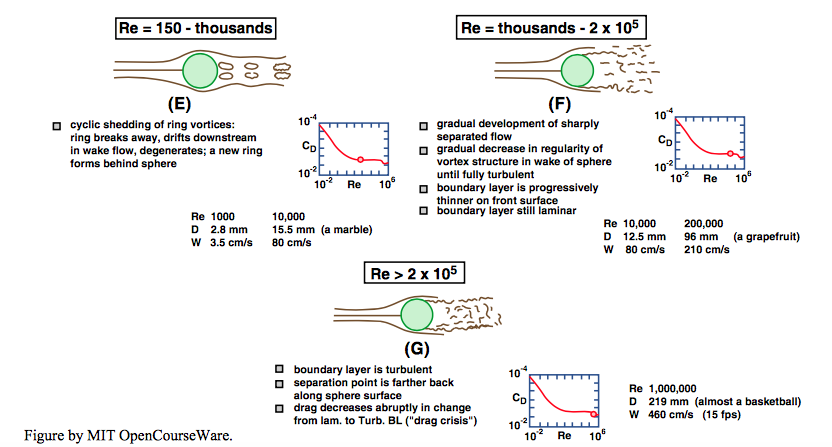
Figure \(\PageIndex{2}\)A shows the picture for creeping flow at \(\text{Re} << 1\), as already discussed. The streamlines show a symmetrical pattern front to back. Although not shown in the figure, the flow velocity increases only gradually away from the surface of the sphere; in other words, there is no well-defined boundary layer at these low Reynolds numbers.
In Figure \(\PageIndex{2}\)B, for \(\text{Re} \approx 1\), the picture is about the same as at lower \(\text{Re}\), but streamlines converge more slowly back of the sphere than they diverge in front of the sphere. Corresponding to this change in flow pattern, it is in about this range that the front-to-back pressure forces begin to increase more rapidly than predicted by Stokes’ Law.
Flow separation can be said to begin at a Reynolds number of about \(24\). The point of separation is at first close to the rear of the sphere, and separation results in the formation of a ring eddy attached to the rear surface of the sphere. Flow within the eddy is at first quite regular and predictable (Figure \(\PageIndex{2}\)C), thus not turbulent, but, as \(\text{Re}\) increases, the point of separation moves to the side of the sphere, and the ring eddy is drawn out in the downstream direction and begins to oscillate and become unstable (Figure \(\PageIndex{2}\)D). At \(\text{Re}\) values of several hundred, the ring eddy is cyclically shed from behind the sphere to drift downstream and decay as another forms (Figure \(\PageIndex{2}\)E). Also in this range of \(\text{Re}\), turbulence begins to develop in the wake of the sphere. At first turbulence develops mainly in the thin zone of strong shearing produced by flow separation and then spreads out downstream, but as \(\text{Re}\) reaches values of a few thousand the entire wake is filled with a mass of turbulent eddies (Figure \(\PageIndex{2}\)F).
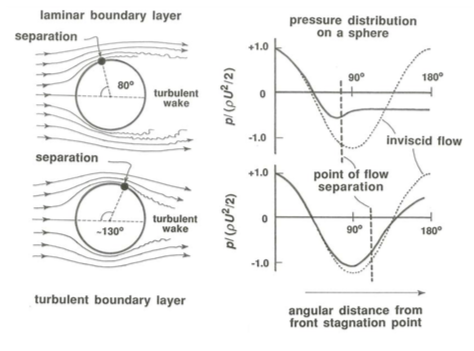
In the range of \(\text{Re}\) from about \(1000\) to about \(200,000\) (Figure \(\PageIndex{2}\)F) the pattern of flow does not change much. The flow separates at a position about \(80^{\circ}\) from the front stagnation point, and there is a fully developed turbulent wake. The drag is due mainly to the pressure distribution on the surface of the sphere, with only a minor contribution from viscous shear stress. The pressure distribution is as shown in Figure \(\PageIndex{3}\) and does not vary much with \(\text{Re}\) in this range, so the drag coefficient remains almost constant at about \(0.5\).
At very high \(\text{Re}\), above about \(200,000\), the boundary layer finally becomes turbulent before separation takes place, and there is a sudden change in the flow pattern (Figure \(\PageIndex{2}\)G). The distinction here is between laminar separation, in which the flow in the boundary layer is still laminar where separation takes place, and turbulent separation, in which the boundary layer has already changed from being laminar to being turbulent at some point upstream of separation. Turbulent separation takes place farther around toward the rear of the sphere, at a position about \(120\)–\(130^{\circ}\) from the front stagnation point. The wake becomes contracted compared to its size when the separation is laminar, and consequently the very low pressure exerted on the surface of the sphere within the separation region acts over a smaller area. Also, the pressure itself in this region is not as low (Figure \(\PageIndex{3}\)). The combined result of these two effects is a sudden drop in the drag coefficient \(C_{D}\), to a minimum of about \(0.1\). This is sometimes called the drag crisis.
Have you ever wondered why golf balls have that pattern of dimples on them? It is to make them go faster and farther, but why? It is because the Reynolds number of the flying golf ball is just about in the range of transition from a laminar boundary layer to a turbulent boundary layer, and the dimples help to trigger the transition and thus reduce the air drag on the flying ball.


