1.2: Pressure
- Page ID
- 4149
The concept of fluid pressure is one of the most fundamental in fluid dynamics. Generally in physics the term pressure is used for a force per unit area. But we need to be more specific about the significance of pressure in fluids.
Fluid Pressure
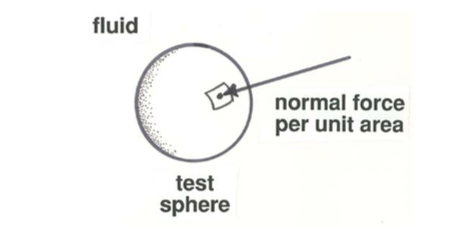
Suppose that you immerse a solid test sphere in a container of fluid at rest, and suppose further that you have a little meter with which you can measure the normal force per unit area exerted by the fluid at some point on the surface of the sphere (Figure \(\PageIndex{1}\)). That force per unit area is the pressure exerted by the fluid on the surface of the sphere. That probably seems like a simple enough concept. (Because the fluid is not moving relative to the sphere, the fluid exerts only a normal component of force, not a tangential component; we will start looking at the nature of the tangential force exerted by moving fluid on a solid surface in the following section.) But there is more to fluid pressure than just that.
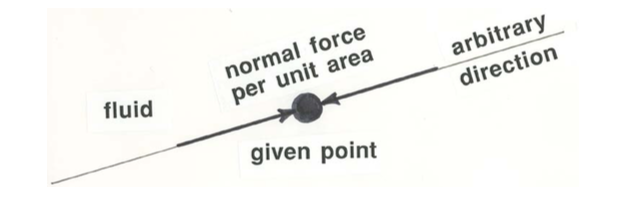
Now suppose that you make the solid sphere smaller and smaller. You can think of it as eventually becoming just a point. Then, associated with each line through that point there is a compressive force per unit area, directed inward from both directions along the line toward the point, with the same value as the force per unit area you measured on the surface of the test sphere (Figure \(\PageIndex{2}\)). And the value of this compressive force per unit area is the same for every orientation of the line through the point. This is the essence of the concept of fluid pressure: it is a compressive force per unit area that acts equally in all directions at a point in the fluid, whether or not there is a solid surface at that point upon which the force acts. If there is no solid surface, you just have to think in terms of one part of the fluid continuum exerting a compressive force on the adjacent part of the fluid continuum.
Pressure of a Moving Fluid
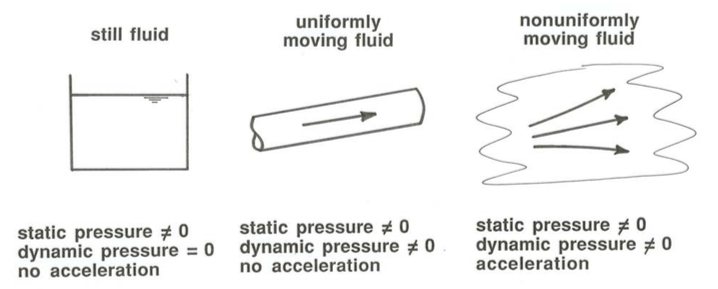
The concept of fluid pressure introduced above holds equally well for a moving fluid. Then you just have to imagine measuring the pressure at a point that is moving along with the fluid. It is convenient and natural to think of the pressure in a moving fluid as being made up of two parts, the static pressure and the dynamic pressure. The static pressure is the pressure that would be measured at the given point in the fluid if the fluid were not moving. The dynamic pressure is the difference between the total pressure—that is, the pressure you would actually measure at the given point in the moving fluid, with some appropriate instrument—and the static pressure. The dynamic pressure is the part of the pressure that is associated with the motion of the fluid. There will be much more to say about the relationship between fluid motion and dynamic pressure later in these notes; suffice it to say here that the dynamic pressure is zero in a stationary fluid, and also in a fluid that is in uniform motion, in the sense that there are no accelerations anywhere in the fluid (Figure \(\PageIndex{3}\)).
Static Pressure
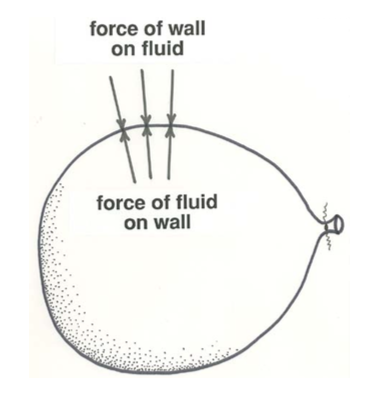
It is not difficult to understand here, however, what determines the static pressure. In the case of fluid in a closed container, one part of the static pressure has to do just with the external compression imposed upon the walls of the container. When you blow up a balloon, the air pressure inside the balloon is greater than outside, because the distended walls of the balloon are trying to re-shrink, and as a consequence they are everywhere pushing inward against the air inside (Figure \(\PageIndex{4}\)). The pressure on the walls becomes adjusted to be the same at all points, because if that were not the case, then there would be pressure differences from point to point within the fluid, and by Newton’s second law that would cause motions in the fluid.
The other part of the static pressure has to do with the weight of fluid that overlies a given point in the fluid. Think about a tall upright cylindrical container filled with a liquid (Figure \(\PageIndex{5}\)). You can easily compute the weight of liquid in the vertical column that overlies a little unit area on the bottom of the container: it is equal to \(p=\rho g h\) (\ref{hydrostatic}), where \(\rho\) is the density of the liquid, \(g\) is the acceleration of gravity, and \(h\) is the height of the liquid column above the bottom:
\begin{equation}
p=\rho g h \label{hydrostatic}
\end{equation}
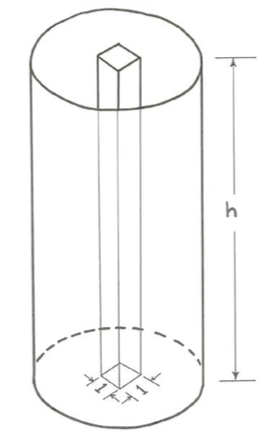
It is just a matter of multiplying the weight per unit volume of the liquid, \(\rho g\), by the volume of liquid in the vertical column, \(h\) (\ref{hydrostatic}). This part of the static pressure caused by the weight of overlying fluid, called the hydrostatic pressure, is given by the same equation not just on the bottom but also at all points in the fluid, and on the sides of the container as well; refer to the discussion, above, of the nature of pressure as a compressive force per unit area acting equally in all directions at any point in the fluid.
So by Equation (\ref{hydrostatic}), called the hydrostatic equation, the hydrostatic pressure in the liquid increases linearly with depth, from zero at the surface (Figure \(\PageIndex{6}\)). Compressible fluids like gases, however, are trickier; the vertical distribution of density and pressure in the atmosphere, for example, is the outcome of the balance between pressure and weight of overlying fluid, on the one hand, and the relationship between pressure and density, on the other hand.
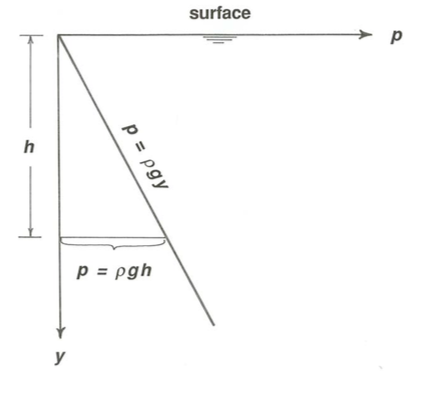
Look again at the container of motionless liquid. In your imagination, isolate a volume of liquid, bounded at the top and bottom by imaginary horizontal planes and around the sides by an imaginary vertical cylinder. Now examine the balance of forces in the vertical direction on the mass of liquid contained within that volume. One thing we know for sure is that the sum of all the vertically directed forces, upward and downward, on that mass of liquid has to be zero, because the liquid is at rest, and Newton’s second law tells us that the net force acting on the volume of liquid must be zero. (This technique of isolating an imaginary volume of material, called a free body, and examining the forces on it and the motions it undergoes is a common technique in the mechanics of continuous media, whether solids or fluids.)
There are vertically directed pressure forces on the top and bottom of the cylinder, but not on the sides of the cylinder, because the pressure forces on the sides of the cylinder are all horizontal. Remember that by the hydrostatic equation the pressure on the bottom of the free body is greater than the pressure on the top. Why, then, does the body not accelerate upward, in accordance with Newton’s second law? The answer is that this upward-directed pressure force is exactly balanced by the weight of the liquid in the body. This is a manifestation of what is called the hydrostatic balance.
Buoyancy
Now suppose that you replace the imaginary free body of liquid with a real body of the same shape, with vanishingly thin but rigid walls and just empty space (if we ignore the density of air) within. The weight of the body is effectively zero, so there is no weight to balance the upward-directed net pressure force. As you all know, the body floats up to the surface. This effect, termed buoyancy, holds for all fluids, gases as well as liquids. It should be easy for you to imagine the great many environments, in and on the Earth, where buoyancy is an important effect.
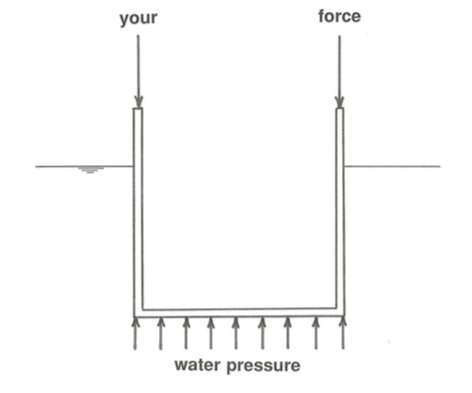
If you want a real-life demonstration of the magnitude of the buoyancy force, try taking a watertight and lightweight pail and pushing it down into a tub full of water, with its open end facing upward (Figure \(\PageIndex{7}\)). You know that the farther in you push it, the more difficult it is to push it. What is going on here is that you are pushing against the force of the hydrostatic pressure summed over the entire bottom surface of the pail. There is no water in the pail to balance that hydrostatic pressure force, so you have to establish the balance with your own hands and arms.
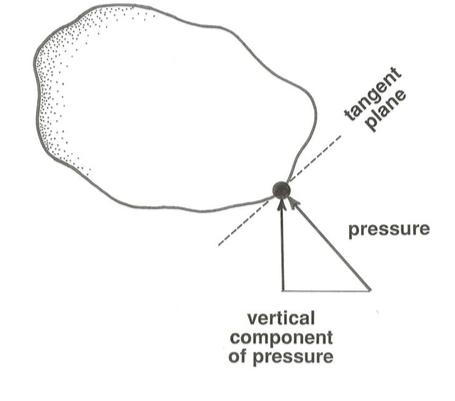
The various bodies within the fluid we have been dealing with need not be of the special shape, with only vertical and horizontal surfaces, we have been assuming. The same considerations hold true for bodies of arbitrary shape. At a point on a sloping part of the surface of such a body, you just have to take the vertical component of the pressure that is acting normal to the surface at the given point, and therefore in a sloping direction (Figure \(\PageIndex{8}\)).
Specific Weight
One final matter has to do with the weight per unit volume, or specific weight, of an object or of some part of a continuous material, usually denoted by \(\gamma\). Because the weight of a body is \(m g\), the specific weight is \(m g/volume\), which can be rearranged as \((m/volume)g\), or \(\rho g\), because density \(\rho\) is just mass per unit volume. So the relationship between density (mass per unit volume) and specific weight (weight per unit volume) is \(\gamma = \rho g\). (Minor note: density could be called “specific mass”, but it never is—although its inverse, the volume per unit mass, is indeed called the specific volume.)
You also have to think about the submerged specific weight of an object that is entirely immersed in a fluid. It should make sense to you, and it follows from the earlier considerations on the pressure forces on submerged bodies, that the effective weight of a submerged body is less than its actual weight by the weight of the fluid it displaces. (This is the effect that I think is supposed to have caused Archimedes to shout “Eureka!” in his bathtub.) In these notes the submerged specific weight is denoted by \(\gamma^{\prime}\). Here is the mathematics:
\begin{equation}
\gamma^{\prime}=\rho_{b o d y} g-\rho_{f l u i d} g=\left(\rho_{b o d y}-\rho_{f l u i d}\right) g
\end{equation}
If this does not make immediate sense to you, just imagine that the density of a certain submerged body, initially denser than the fluid, is gradually decreased somehow until its density is the same as that of the fluid, whereupon it has the same specific weight as the fluid and is in hydrostatic balance, and therefore neither rises nor sinks. A body of this kind is said to be neutrally buoyant. Tiny neutrally buoyant particles make excellent markers for tracing and visualizing the motions of fluids, both in reality and in the imagination.


