Appendix a • Scientific Tools
- Page ID
- 10994
Many physical sciences including atmospheric science share the same fundamental definitions and analysis techniques. These fundamentals include problem-solving methods, standard units, ways of expressing relationships, formats for plotting the results, measurement uncertainty, and error propagation. The fundamentals reviewed here are used throughout this book.
The following method aids understanding the problem, speeds solution, and helps to avoid errors. This method is used throughout the book in the various Sample Applications.
- List the “Given” variables with their symbols, values and units.
- List the unknown variables to “Find”, with units.
- Sketch the objects, velocities, etc. if appropriate.
- Determine which equation(s) contains the unknown variable as a function of the knowns. This equation might need to be rearranged to solve for the unknown. If the solution equation contains more unknowns, find additional equations for them.
- Make assumptions, if necessary, for any of the unknowns for which you have no equations. Clearly state your assumptions, and justify them.
- Solve the equations using the known or assumed values, being sure to carry along the units. Show your intermediate steps.
- Identify the final answer by putting a box around it, underlining it, or making it bold face.
- Check your answer. If the solved units don’t match the desired units of the unknown, then either a mistake was made, or unit conversion might be needed (e.g., convert from knots to m s–1). Also, certain functions such as “ln” and “exp” require arguments that are dimensionless, while trig functions like “sine” need an argument in degrees or radians. These are clues to help catch mistakes. Also, compare your answer with your sketch, to check if it is physically reasonable. Check other physical constraints (e.g., humidities cannot be negative, speeds cannot be infinite).
- Discuss the significance of the answer.
A.1. Dimensions and Units
A.1.1. Standards
| Table A-1. Basic dimensions and their SI units. | ||
| Dimension | Unit | Abbrev. |
|---|---|---|
|
length mass time electrical current temperature (thermodynamic) amount of substance luminous intensity |
meter kilogram second ampere kelvin mole candela |
m kg s A K mol cd |
| Table A-2. Some derived dimensions & their SI units. | ||
| Dimension | Unit (Abbrev. | Composition |
|---|---|---|
|
force energy power pressure, stress temperature |
newton (N) joule (J) watt (W) pascal (Pa) degree Celsius (°C) |
kg·m·s–2 kg·m2·s–2 kg·m2·s–3 kg·m–1·s–2 T(K) – 273.15 |
|
frequency electric charge electric potential electric resistance |
hertz (Hz) coulomb (C) volt (V) ohm (Ω) |
s–1 s·A m2·kg·s–3·A–1 m2·kg·s–3·A–2 |
|
plane angle solid angle |
radian (rad) steradian (sr) |
m·m–1 m2·m–2 |
| Table A-3. Prefixes. (*Size is in terms of USA “short scale” designations. Some international “long scale” designations are shown in italics, if different.) | |||
| Multiplier | Size* | Unit | Abbrev. |
|---|---|---|---|
|
1024 1021 1018 1015 1012 109 106 103 102 101 |
septillion (quadrillion) sextillion (trilliard) quintillion (trillion) quadrillion (billiard) trillion (billion) billion (milliard) million thousand hundred ten |
yotta zetta exa peta tera giga mega kilo hecto deka |
Y Z E P T G M k h da |
|
10–1 10–2 10–3 10–6 10–9 10–12 10–15 10–18 10–21 10–24 |
tenth hundredth thousandth millionth billionth trillionth quadrillionth quintillionth sextillionth septillionth |
deci centi milli micro nano pico femto atto zepto yocto |
d c m μ n p f a z y |
| Table A-4. Some other units. (* unofficial symbol) | ||
| Name | Symbol | Value in SI units |
|---|---|---|
|
minute hour day degree (angle) liter (or litre) metric ton (or tonne) astronomical unit ångström nautical mile knot hectare bar |
min h d ° L t ua Å nm* kt* ha bar |
1 min = 60 s 1 h = 60 min = 3600 s 1 d = 24 h = 86,400 s 1° = (π/180) rad 1 L = 10–3 m3 1 t = 103 kg 1 ua ≈ 1.49598 x 1011 m 1 Å = 10–10 m 1 naut. mile = 1852 m 1 knot = (1852 m / 3600 s) 1 ha = 104 m2 1 bar = 100 kPa = 105 Pa |
The IEEE Standards Board officially adopted the SI short-scale units of Table A-3. E.g., 1 kilobit = 1000 bits.
But historically, manufacturers have referred to
210 bits (=1,024 bits) as 1 kilobit (NOT SI standard),
220 bits (=1,048,576) as 1 megabit (NOT SI standard),
230 bits (=1,073,741,824) as 1 gigabit (NOT SI std.).
A.1.2. Unit Conversion
You can create ratios of equivalent values to enable easy unit conversion. For example, a velocity of 1 knot equals 0.51 m s–1. Because these two values equal, their ratio must be one:
\begin{align}1=\frac{(1 \mathrm{knot})}{\left(0.51 \mathrm{m} \mathrm{s}^{-1}\right)}\tag{A.2}\end{align}
Although the numbers 1 and 0.51 do NOT equal each other (and their ratio does NOT equal 1), the values include the units, and hence the ratio of values does equal 1.
The inverse of 1 is 1, thus, it makes no difference which value appears in the numerator. For example:
\begin{align}1=\frac{\left(0.51 \mathrm{m} \mathrm{s}^{-1}\right)}{(1 \mathrm{knot})}\tag{A.3}\end{align}
When any quantity is multiplied by 1, its value does not change. Hence, by multiplying a velocity by the ratio in eqs. (A.2) or (A.3), we can change the units without changing the physics or the value.
Even if a conversion relationship is not known, you can sometimes figure it out if you know equivalent values that apply to a situation. For example, what is the conversion between pressure in “pounds per square inch” (PSI) and in “inches of mercury” (in Hg). Perhaps you might already know that the average pressure at sea level is 14.7 PSI. You might also know that standard sea-level pressure is 29.92 in Hg. Thus, these two values are equivalent at sea level, and their ratio gives the conversion between them:
\(\ 1=\frac{(14.7 \mathrm{PSI})}{(29.92 \mathrm{in} \mathrm{Hg})}=0.49 \frac{(\mathrm{PSI})}{(\mathrm{in} \mathrm{Hg})}\)
or 1 in Hg = 0.49 PSI.
Ratios can also be formed to add or remove prefixes and magnitudes to units. For example, 1 milligram (mg) equals 0.001 grams, by definition. Thus their ratio is one. We can use this ratio to find 5 x 107 mg in units of kg. For example:
\(\ \left(5 x 10^{7} \mathrm{mg}\right) \cdot \frac{0.001 \&}{1 \mathrm{mg}} \cdot \frac{1 \mathrm{kg}}{1000 \mathrm{g}}=50 \mathrm{kg}\)
This trick of forming ratios to do conversions works only when both units have the same zero point. In the example above, 0 PSI = 0 in Hg. Similarly, 0 m s–1 = 0 knots. This trick fails for temperature conversions, because °F, °C, and K all have different zero points. Namely, they have additive and multiplicative factors. For temperature conversions, you must use special conversion formulae, as described in the “Relationships and Graphs” section.
Sample Application
Convert a wind speed of 10 knots into m s–1.
Find the Answer
Given: M = 10 kt wind speed
Find: M = ? m s–1
Multiply wind speed by 1 in the form of eq. (A.3):
\begin{aligned}
M &=10 \mathrm{kt}=(10 \mathrm{kt}) \cdot 1 \\
&=(10 \mathrm{kt}) \cdot\left(\frac{0.51 \mathrm{m} / \mathrm{s}}{1 \mathrm{kt}}\right) \\
&=\left(\frac{10 \cdot 0.51}{1}\right) \cdot\left(\frac{\mathrm{kt} \cdot(\mathrm{m} / \mathrm{s})}{\mathrm{kt}}\right) \quad \text { grouping } \\
&=\underline{\bf{5.1 \mathrm{m} \mathrm{s}^{-1}}}
\end{aligned}
Check: Units OK. Physically reasonable.
Exposition: Note how we grouped the numbers separately from the units. You can calculate the number group using your calculator. You can reduce the units group by canceling identical units in the numerator and denominator (such as knots, in this example).
How do you know whether to use (A.2) or (A.3)? Given a value with knots in the numerator, we want to multiply it by a ratio that has knots in the denominator, so that the knots will cancel. Eq. (A.3) will work.
Sample Application
Sometimes you can use units to guess the form of an equation. For example, metabolic heat-production rate by humans sitting quietly is about 100 watts. Find the number of calories produced in half a day.
Find the Answer
Given: C = 100 W, ∆t = 0.5 d
Find: B = ? cal heat production
Eqs: From tables of unit conversion in other books 1 W = 14.3353 cal min–1, 1 h = 60 min, & 1 d = 24 h
By forming each of these equivalences as ratios, you can convert from watts into calories, and then from minutes into hours into days:
\begin{aligned}
C &=(100 \mathrm{W}) \cdot\left(\frac{14.3353 \mathrm{cal} / \mathrm{min}}{1 \mathrm{W}}\right) \cdot\left(\frac{60 \mathrm{min}}{1 \mathrm{y}}\right) \cdot\left(\frac{24 \mathrm{b}}{1 \mathrm{d}}\right) \\
&=2.06 \times 10^{6} \mathrm{cal}\ \mathrm{d}^{-1}
\end{aligned}
By looking at the units of the last line it is obvious that if we multiply it by the time ∆t in days, then we will be left with our desired units of calories. Thus, the final equation is:
Check: Units OK. Physically reasonable
Exposition: Over a million calories of heat is given off by a human sitting still for half a day. The number of calories of food we eat should be sufficient to replace those calories burned metabolically. Caution: “calories” listed on food packages are really kilocalories.
A.2. FUNCTIONS AND FINITE DIFFERENCE
As in other fields of science and engineering, functional relationships describe how one variable (the dependent variable) changes when one or more other variables (the independent variables) change. Suppose that P2 is the pressure at time t2, and P1 is the pressure at time t1. Pressure “varies” with time, or “is a function of time”. Such functional dependence is written generically as P(t). For a single value of pressure that occurs at specific time, such as at t = 50 s, the notation P(50 s) is used.
The symbol ∆ means change or difference. Differences must always be taken in the same direction relative to the independent variable. For example, if temperature T and pressure P both vary with time t, then ∆T and ∆P are defined as their values at the later time minus their values at the earlier time. For example, ∆T = T(t2) – T(t1), and ∆P = P(t2) – P(t1), where t2 is later than t1. The notation is sometimes simplified to be ∆T = T2 – T1 and ∆P = P2 – P1 for ∆t = t2 – t1.
In a different example, let temperature T depend on independent variable height z. Then
∆T = T(z2) – T(z1) = T2 – T1
and
∆z = z2 – z1
where z2 is higher than z1. Furthermore, a ratio such as ∆T/∆z is equivalent to (T2 – T1)/(z2 – z1), or [T(z2) – T(z1)]/(z2 – z1), where the differences in the numerator and denominator must always be taken in the same direction (e.g., point 2 – point 1). Don’t be deceived into subtracting the smaller value from the larger one when you compute a finite difference, because if you do, the sign of your answer might be wrong (see the Sample Application on this page).
The change of something with distance is called a gradient. Thus, ∆T/∆z is a vertical temperature gradient. Similarly, ∆T/∆x is a horizontal temperature gradient.
Although calculus is a useful mathematical tool for studying the physics of the atmosphere, this book is designed for an audience who might not be familiar with calculus. In the place of differential calculus we will use finite differences, ∆. In place of integral calculus, we will use sums or graphically examine the area under curves.
For those students with a calculus background, “HIGHER MATH” boxes are scattered here and there in the book to provide a taste of theoretical meteorology. These “HIGHER MATH” boxes are surrounded by a thick line as shown at left, and may be safely skipped by students wishing to avoid calculus.
Sample Application
Suppose the air at the ground has a temperature of 20°C, while the air at height 500 m is 15 °C. Find the vertical temperature gradient.
Find the Answer
Given:
z2 = 500 m top altitude
z1 = 0 m ground altitude
T2 = T(z2) = 15 °C temperature at 500 m altitude
T1 = T(z1) = 20 °C temperature at ground
Find: ∆T/∆z = ? °C m–1
temperature gradient
Sketch:
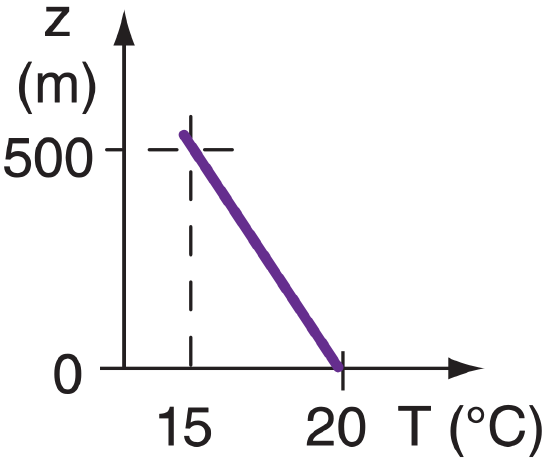 Use definition of a gradient:
Use definition of a gradient:
∆T/∆z = ( T2 – T1 ) / ( z2 – z1 )
= (15°C – 20°C) / (500 m – 0 m)
Check: Units OK. Sketch OK. Sign negative.
Exposition: If this gradient is constant with height, then the temperature at your head is 0.02°C colder than at your toes, assuming you are roughly 2m tall.
CAUTION: Suppose you erroneously had computed the gradient as (20 – 15°C) / (500 – 0 m). Then your answer would have had the wrong sign, because you had erroneously computed (T1–T2)/(z2–z1) instead of the desired (T2–T1)/(z2–z1). Always form your differences in the same order (point 2 – point 1) in both the numerator and denominator.
In theoretical meteorology, the physics of the atmosphere is described by differential equations. Outside of these “HIGHER MATH” boxes, we utilize the following approximations to avoid calculus.
A derivative can be approximated as:
\(\ \frac{\partial T}{\partial z} \approx \frac{\Delta T}{\Delta z} \quad \text { for small } \Delta z\)
A total derivative:
\(\ \frac{d T}{d t}=\frac{\partial T}{\partial t}+U \frac{\partial T}{\partial x}+V \frac{\partial T}{\partial y}+W \frac{\partial T}{\partial z}\)
is approximated as:
\(\ \approx \frac{\Delta T}{\Delta t}+U \frac{\Delta T}{\Delta x}+V \frac{\Delta T}{\Delta y}+W \frac{\Delta T}{\Delta z}\)
Also, you can approximate an integral by a sum:
\(\ \int T d z \approx \sum T(z) \cdot \Delta z\)
where T is temperature, z is height, t is time, (U, V, W) are wind components in the (x, y, z) directions, which are positive toward the (east, north, up).
A.3. RELATIONSHIPS AND GRAPHS
Although T(z) says that there is some functional relationship between temperature T and height z, it does not specify what that relationship is. Temperature could increase as height increases. It could decrease as height increases. It could increase with the square of height. It could vary logarithmically with height.
The particular form of the function might be governed by some underlying physics, and have a fixed functional form that is sometimes called a physical “law” or a mathematical definition. Other relationships can be found by plotting observational data.
Linear, semi-log and log-log graphs are frequently used to discover and display relationships between dependent and independent variables.
A.3.1. Linear
A linear relationship yields a straight line on a linear graph (values along both axes increase at constant rates with distance from the origin).
For example, the relationship between temperature in degrees Celsius and Fahrenheit is linear; namely, temperature in Fahrenheit is proportional to the first power of temperature in Celsius
\begin{align} T_{{\circ}F}=a \cdot T_{\circ C}+b\tag{A.4}\end{align}
where the parameters in this equation are a = 9/5 (°F/°C) and b = 32 °F, see Fig. A.1.
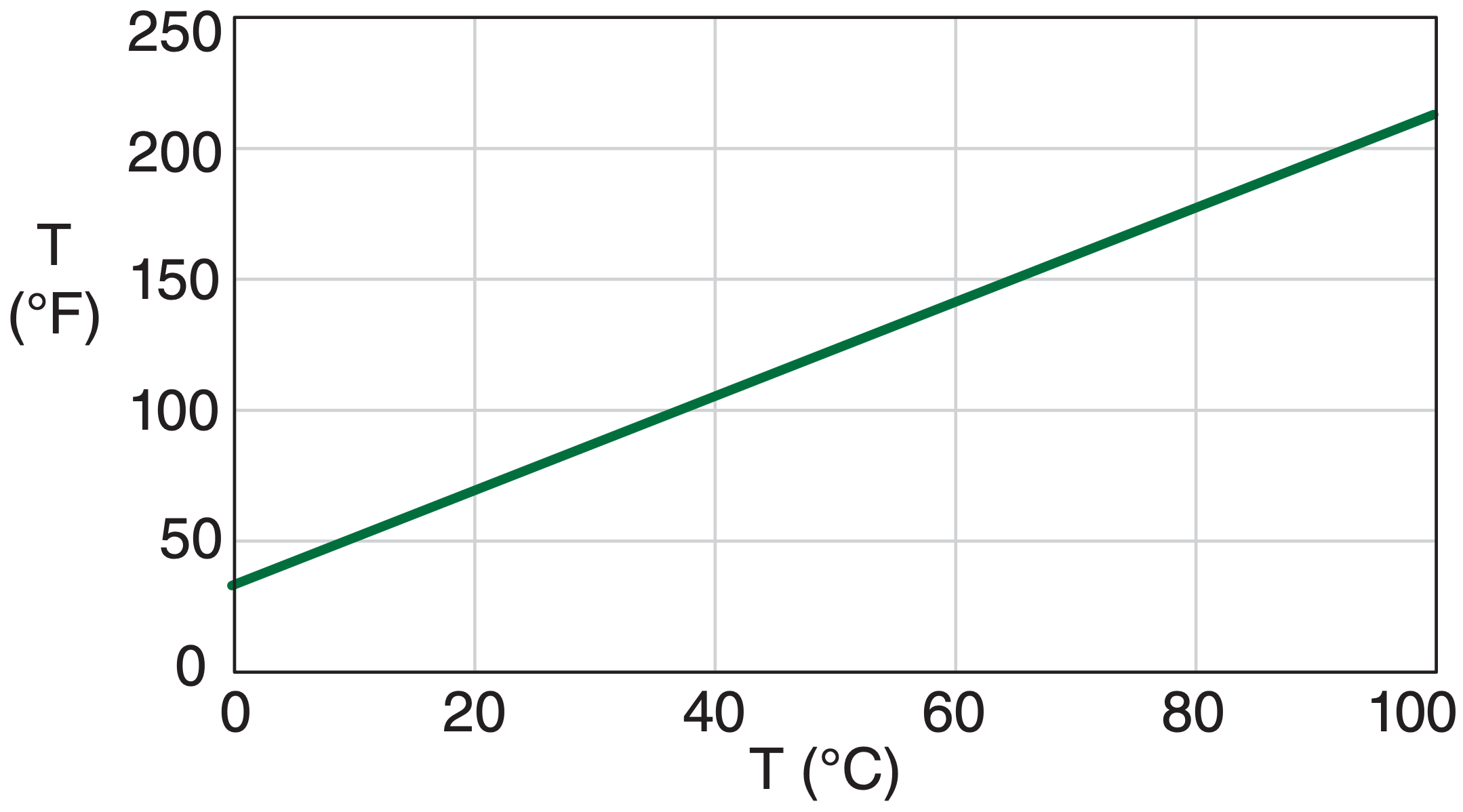
Sample Application
Convert 10°C to Fahrenheit.
Find the Answer
Given: T°C = 10°C. Find: T°F = ? °F
Sketch: (see Fig A.1). Use eq. (A.4):
T°F = a·T°C + b
= (9/5 °F/°C)·(10°C) + 32°F
= 18°F + 32°F = 50°F
Check: Units OK. Sketch OK. Physics OK.
Exposition: As the temperature in Celsius increases by equal amounts of 10°C, the corresponding Fahrenheit values increase in equal amounts of 18°F. Such a constant rate of increase of the dependent variable for a constant rate of increase of independent variable indicates a linear relationship.
The slope (change in values along the vertical axis per change of values along the horizontal axis) of the line equals the factor a, which is 9/5 in this case. As shown in Fig. A.1, the nonzero parameter b causes the plotted line to cross the vertical axis not at the origin (T°C, T°F) = (0, 0), but at an intercept of T = 32°F [i.e., at point (0°C, 32°F].
The relationship between temperature in degrees Celsius and absolute temperature in Kelvins is also linear:
\begin{align}T(\mathrm{K})=T\left(^{\circ} \mathrm{C}\right)+273.15\tag{A.5}\end{align}
If plotted on a linear graph, the slope would be 1 and the intercept is 273 K. Most equations using temperature require the use of absolute temperature.
A.3.2. Logarithmic
An exponential or logarithmic relationship gives a straight line when plotted on a semi-log graph (one axis is linear, the other is logarithmic).
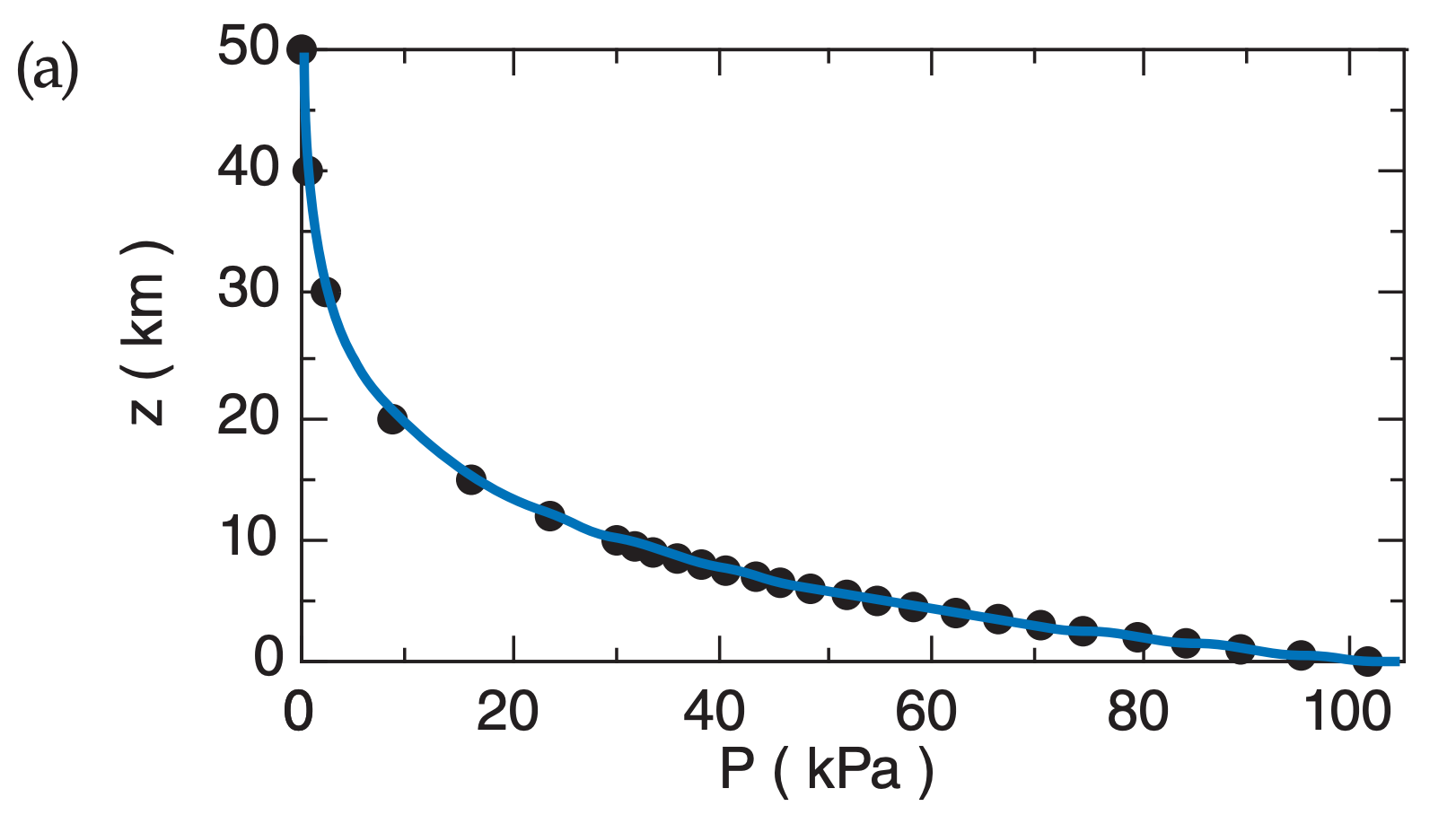

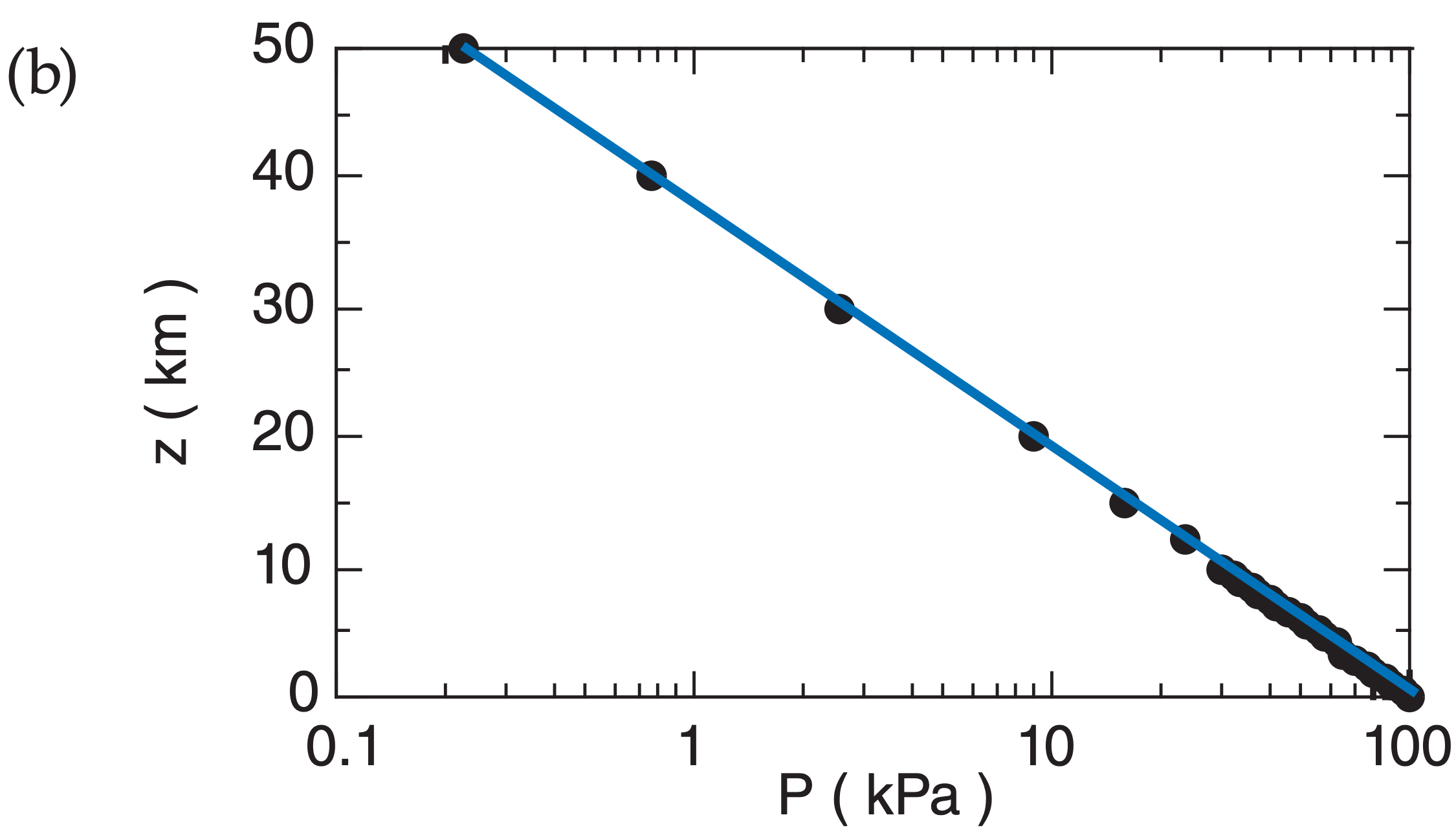
For example, the decrease of pressure with height is logarithmic (Fig. A.2) in atmospheres where the temperature is constant with height:
\begin{align}\ln \left(\frac{P}{P_{o}}\right)=\frac{-a}{T} \cdot z\tag{A.6}\end{align}
where a = 0.0342 K m–1, Po = 101.3 kPa for Earth, and average temperature T must be in Kelvin.
symbol a in this equation has a different value than in the previous equation. I often re-use symbols in this book, because there are not enough symbols for all the variables.
Sample Application
At what height does P = 50 kPa, given T = 0°C?
Find the Answer
Given: P = 50 kPa, T = 0 + 273.15 = 273.15 K.
Find: z = ? km
Solve eq. (A.6) for z: z = (T/a) · ln(Po/P)
z = [(273.15K) / (0.0342 K m–1)] · ln(101.3kPa/50kPa)
= (7987 m) · ln(2.026) = 5639 m = 5.6 km.
Check: Units OK. Agrees with Fig. A.2.
Exposition: At this height the air is so thin that people would die of hypoxia (lack of oxygen) unless they breath pressurized oxygen.
Fig. A.2 plots the relationship between P and z in both linear and semi-log graphs, for T = 280 K. Pressure decreases rapidly with height near the ground, but decreases more slowly at higher altitude.
From Fig. A.2a we see that the portion of the curve in the lowest 3 km of the atmosphere is almost a straight line, and conclude that the variation of pressure with height is nearly linear in that region. Near the ground, the pressure decreases roughly 10 kPa with each 1 km height gain.
Fig. A.2b plots P with a logarithmic scale along the bottom axis, and plots z with a linear scale on the vertical axis. All of the data points at all heights fall on a straight line on this graph. This is evidence that the logarithm of P is proportional to z.
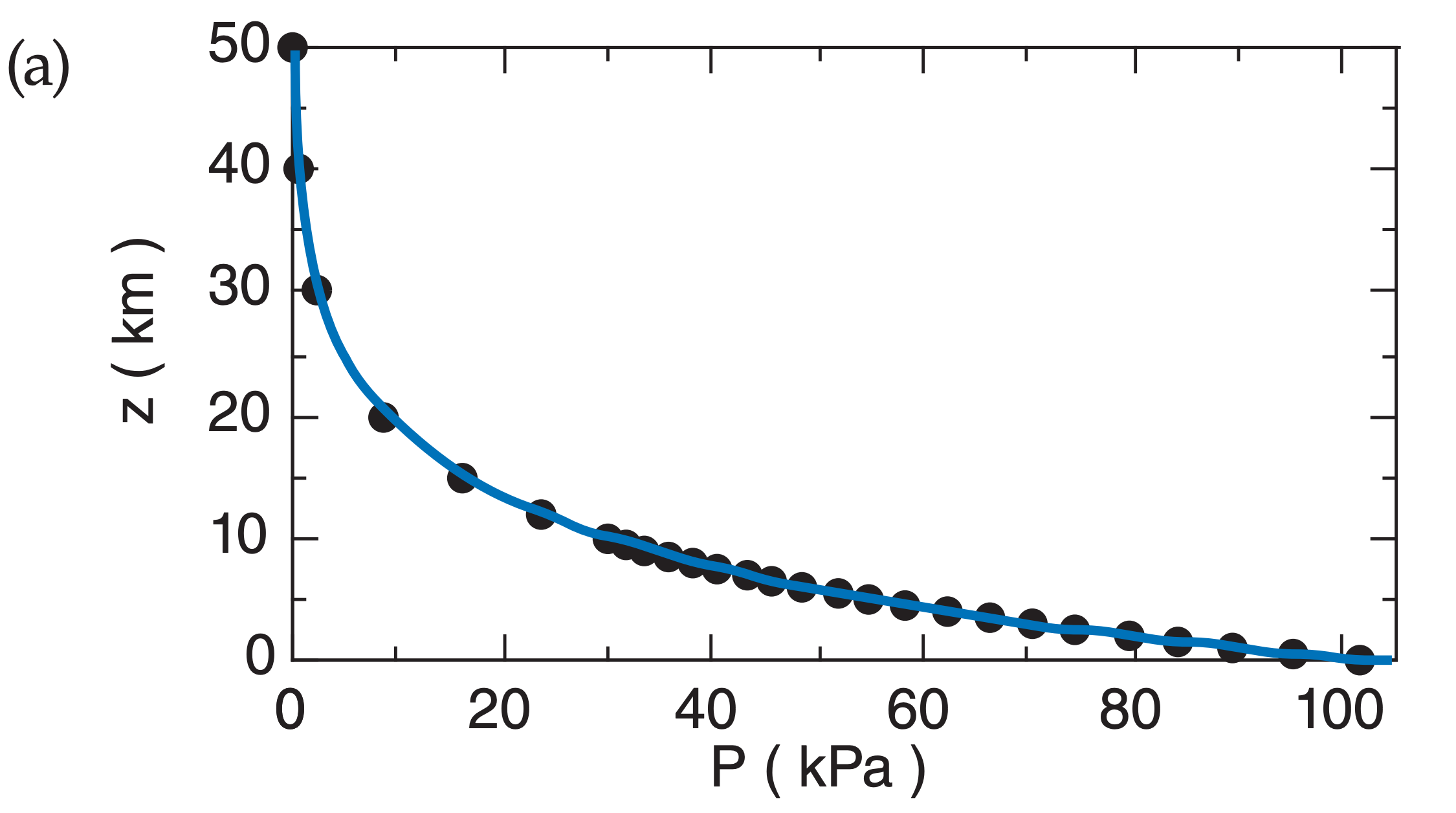
A.3.3. Power
If the dependent variable is proportional to a power of the independent variable, then the data will appear as a straight line on a log-log graph (both axes are logarithmic).
For example, Johannes Kepler, the 17th century astronomer, discovered that planets in the solar system have elliptical orbits around the sun, and that the time period Y of each orbit is related to the average distance R of the planet from the sun by:
\begin{align}Y=a \cdot R^{3 / 2}\tag{A.7}\end{align}
Parameter a ≈ 0.1996 d·(Gm)–3/2, where d is the abbreviation for Earth days and Gm is gigameters (= 106 km).
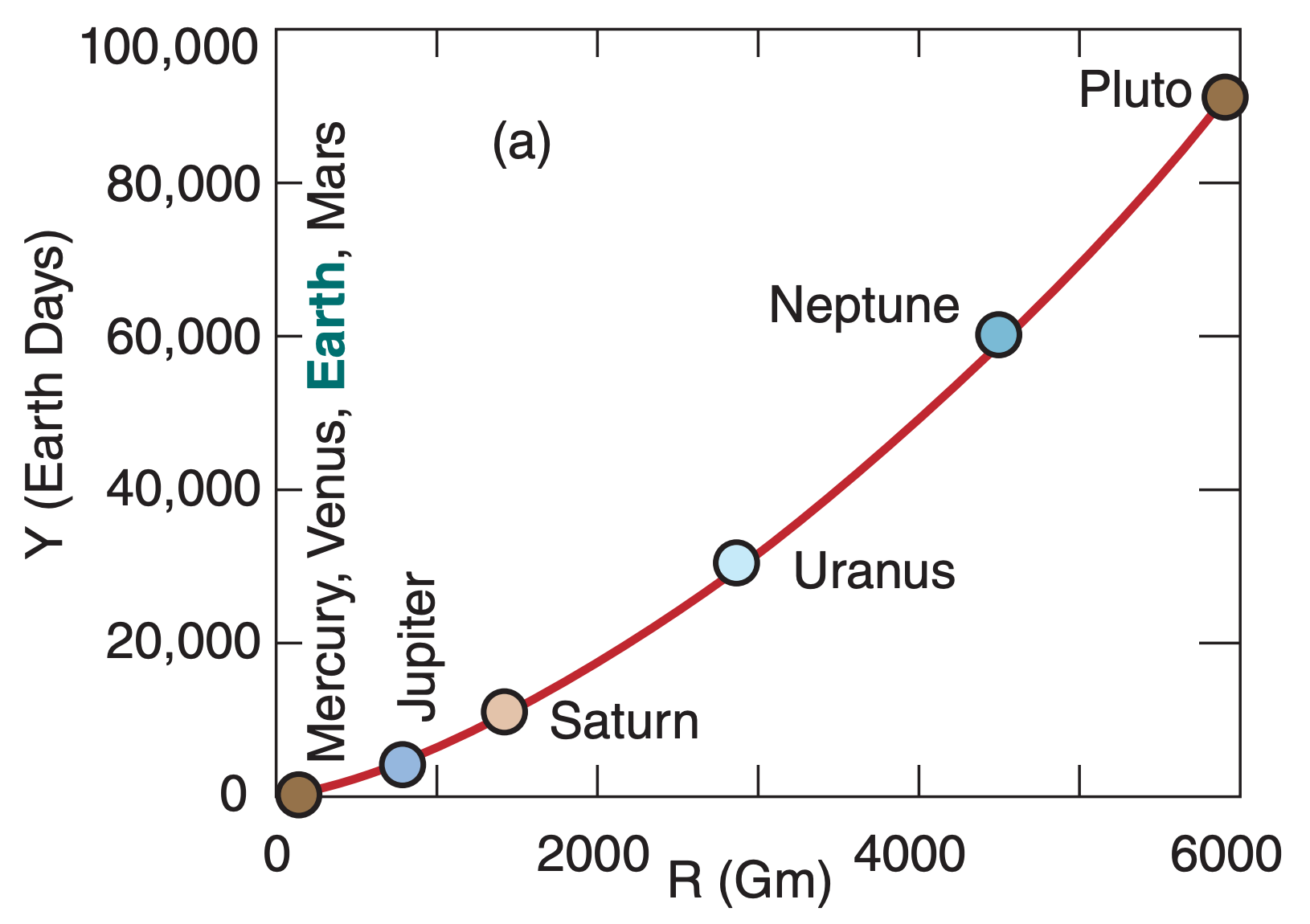
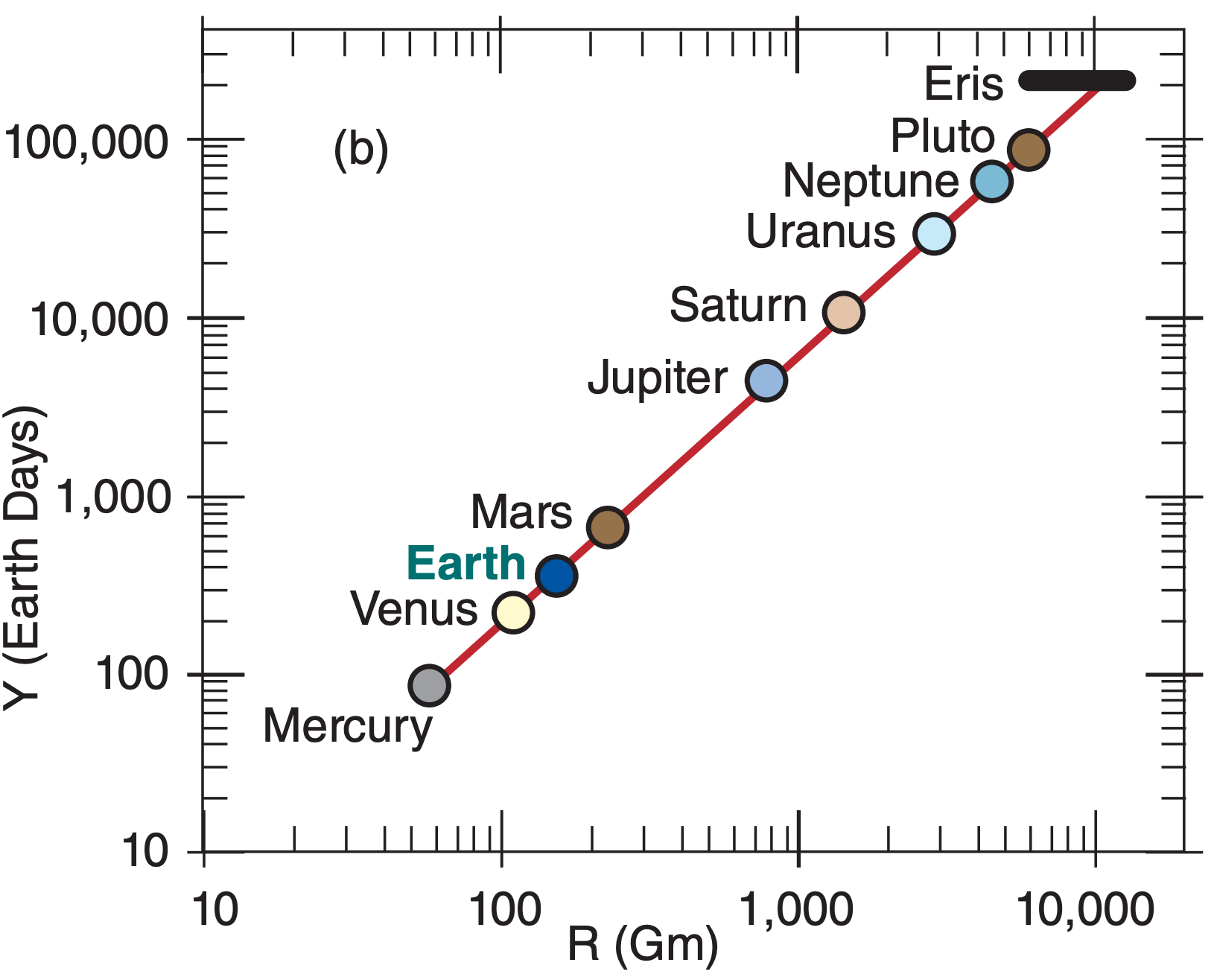
Using a table of the average distance of the planets from the sun (see Apply exercise A1 in the Radiation chapter), you can calculate orbital period using eq. (A.7). These are plotted in Fig. A.3a on a linear graph, and in Fig. A.3b on a log-log graph (copied from the “Solar & IR Radiation” chapter).
The slope of the straight line on the log-log graph (Fig. A.3b) equals the power of the exponent. Namely, the range of orbital periods between Mercury and Pluto is about 3 cycles (i.e., 3 orders of magnitude, such as 100 to 1,000 to 10,000 to 100,000), while the range of distances from the sun is 2 cycles. Thus, the slope is 3 to 2, as indicated in eq. (A.7).
Sample Application
Find the orbital period of Mercury (R = 58 Gm).
Find the Answer
Given: R = 58 Gm. Find: Y = ? d
Use eq.(A.7): Y = [0.1996 d·(Gm)–3/2] · (58 Gm)3/2 = 88d
Check: Units OK. Agrees with Fig. A.3
Exposition: 4 orbits of Mercury per each Earth orbit.
A.4. ERRORS
Error is the difference between a measured (or estimated) value and the true (or reference) value.
A.4.1. Systematic Error & Accuracy
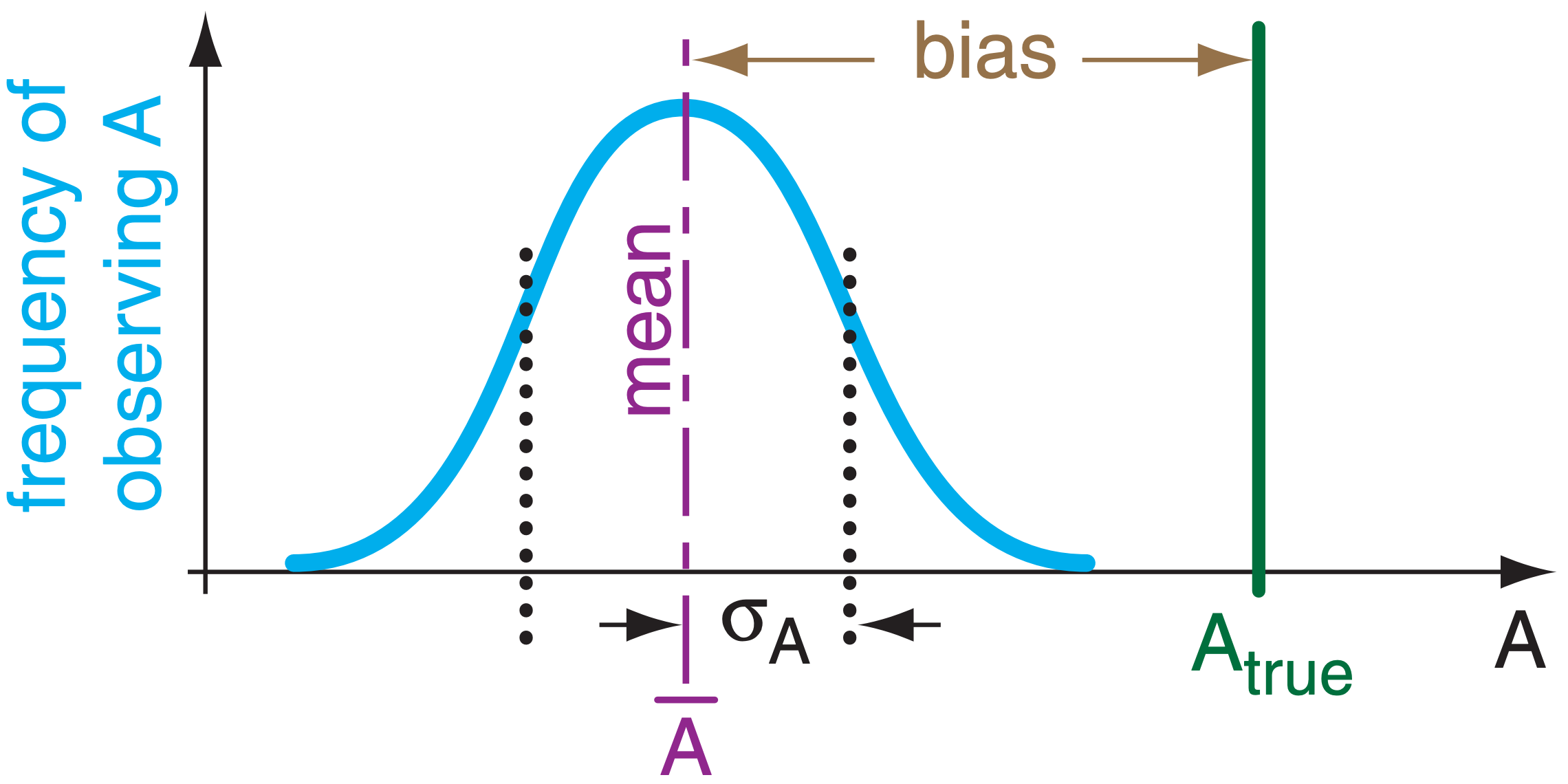
If part of the error is systematic or repeatable (namely, you get the same error each time you make a measurement), then the difference between the average measurement and the true value is called the bias. Smaller bias magnitude (i.e., lower systematic errors) corresponds to greater accuracy. Namely, accuracy indicates how close your average observations are to truth (Fig. A4).
Systematic errors can be due to errors in instrument calibration, personal errors (such as parallax error in reading a dial), erroneous experimental conditions (such as not shielding a thermometer from sunlight), and imperfect technique (such as breathing on a thermometer before you read it).
If you can calculate or otherwise know the bias, then you can remove this bias from your observations to correct for systematic error. Namely, you can easily make your corrected observations more accurate.
A.4.2. Random Error & Precision
After removing systematic errors, you might find that your observations still have some unexplained variability from measurement to measurement. These are called random errors (Fig. A.4). Experiments with smaller random errors are said to have higher precision; namely, they are more precise. The standard deviation (or spread) of your observations is a measure of the random error — greater standard deviation indicates greater random error and lower precision.
Random errors can be due to errors in judgment (such as by manually reading a dial with poor resolution), fluctuating conditions (such as trying to determine sea level on a wavy ocean), small disturbances (such mechanical vibrations of an instrumented tower in high winds), and errors in definition (such as measuring the dimension of a fractal-shaped cloud, which depends on the size of the measuring stick).
Unfortunately, the probabilistic nature of random errors makes them difficult to remove after the fact. Often, the only recourse is to repeat the experiment under better controlled conditions and with higher quality instruments, and be sure to take a large number of observations to improve the statistical robustness of your results.
A.4.3. Reporting Observations
For any variable A that you have measured N times to yield a data set (A1, A2, A3, ..., AN), let A be the mean value, and σA be the standard deviation. These are defined as:
\begin{align}\bar{A}=\frac{1}{N} \sum_{i=1}^{N} A_{i}\tag{A.8}\end{align}
and
\begin{align}\sigma_{A}=\left[\frac{1}{(N-1)} \sum_{i=1}^{N}(A-\bar{A})^{2}\right]^{1 / 2}\tag{A.9}\end{align}
where i is a dummy index that points to a single data element Ai in your data set.
After removing any known biases, the resulting observation is usually reported or written as a mean (average) value plus or minus (±) the standard deviation:
\begin{align}A=\bar{A} \pm \sigma_{A}\tag{A.10}\end{align}
where the precision or standard uncertainty is given by the standard deviation σA.
Sample Application
Given these T observations: (15, 13, 20, 12, 10, 17, 18)°C. Ttrue = 8°C. Find the mean, bias & std dev.
Find the Answer
Given: Ttrue = 8°C, and the data set above.
Find: \(\ \overline{T}\) = ? °C, σT = ? °C, bias = ? °C.
Use eq. (A.8): \(\ \overline{T}\) = (1/7)(15+13+20+12+10+17+18) = 15°C
Define the deviation from mean as: \(\ T^{\prime}=T-\bar{T}\)
Thus, our observation have T’ = (0, –2, 5, –3, –5, 2, 3)°C
Use eq. (A.9), rewritten as σT = [(N–1)–1 Σ(A’ 2)]1/2
Thus: σT = [(1/6) · (0+4+25+9+25+4+9)(°C)2] 1/2 = 3.56°C
From the raw observations: T = 15 ± 3.56 °C .
Bias = \(\ \overline{T}-T_{t r u e}=15-8^{\circ} \mathrm{C}=\underline{\bf{7^{\circ} \mathrm{C}}} \)
Check: Units OK. We seem to have a warm bias.
Exposition: Our observations are not accurate (large bias) and are not precise (large σT).
Similarly, the mean and standard deviation of some other variable B would be \(\ \overline{B}\) and σB.
For example, Newton’s constant of gravitation G is reported (CODATA 2006) as:
G = 6.67428x10–11 ± 0.00067x10–11 m3 kg–1 s–2 .
Suppose D is a function of A , B and C, where C is not a constant. Namely, D(A, B, C).
If the error standard deviations σA, σB, and σC for A, B & C are known, then the propagation of errors into the standard deviation σD of variable D is:
\begin{align}\sigma_{D}=\left[\left(\frac{\partial D}{\partial A}\right)^{2} \cdot \sigma_{A}^{2}+\left(\frac{\partial D}{\partial B}\right)^{2} \cdot \sigma_{B}^{2}+\left(\frac{\partial D}{\partial C}\right)^{2} \cdot \sigma_{C}^{2}\right.
+2 r_{A B} \cdot\left(\frac{\partial D}{\partial A}\right) \cdot\left(\frac{\partial D}{\partial B}\right) \cdot \sigma_{A} \cdot \sigma_{B}
+2 r_{A C} \cdot\left(\frac{\partial D}{\partial A}\right) \cdot\left(\frac{\partial D}{\partial C}\right) \cdot \sigma_{A} \cdot \sigma_{C}
\left.+2 r_{B C} \cdot\left(\frac{\partial D}{\partial B}\right) \cdot\left(\frac{\partial D}{\partial C}\right) \cdot \sigma_{B} \cdot \sigma_{C}\right]^{1 / 2}
\tag{A.a}\end{align}
The correlation coefficients r are defined as
\(\ r_{A B}=\frac{1}{(N-1) \cdot \sigma_{A} \cdot \sigma_{B}} \cdot \sum_{i=1}^{N}\left[\left(A_{i}-\bar{A}\right) \cdot\left(B_{i}-\bar{B}\right)\right]\)
and correlations rBC and rAC are defined similarly. If A and B are independent, then rAB = 0. Correlations between the other variables could also be zero.
For example, suppose you measure air density \(\ \left(\rho=\bar{\rho} \pm \sigma_{\rho}\right)\) and temperature \(\ \left(T=\bar{T} \pm \sigma_{T}\right)\), and calculate pressure (P) using the ideal gas law P = ρ·ℜ·T, where ℜ is a constant. Thus, from calculus: ∂P/∂ρ = ℜ·T, and ∂P/∂T = ρ·ℜ. Assume ρ and T are independent, thus the correlation coefficient rρT = 0.
Our best estimate of pressure is
\(\ \bar{P}=\bar{\rho} \cdot \Re \cdot \bar{T}\)
To estimate the pressure error σP, use eq. (A.a) to propagate the other errors into the pressure error:
\(\ \begin{aligned}
&\sigma_{P}=\left[\left(\frac{\partial P}{\partial \rho}\right)^{2} \cdot \sigma_{\rho}^{2}+\left(\frac{\partial P}{\partial T}\right)^{2} \cdot \sigma_{T}^{2}\right]^{1 / 2}\\
&\sigma_{P}=\left[(\Re \cdot T)^{2} \cdot \sigma_{\rho}^{2}+(\Re \cdot \rho)^{2} \cdot \sigma_{T}^{2}\right]^{1 / 2}
\end{aligned}\)
Multiply the right side by 1 in the form of \(\ \bar{P} /(\bar{\rho} \cdot \mathfrak{R} \cdot \bar{T})\)
\begin{aligned}
&\sigma_{P}=\bar{P} \cdot\left[\left(\frac{1}{\rho}\right)^{2} \cdot \sigma_{\rho}^{2}+\left(\frac{1}{\bar{T}}\right)^{2} \cdot \sigma_{T}^{2}\right]^{1 / 2}\\ or\\
&\sigma_{P}=\bar{P} \cdot\left[\left(\sigma_{\rho} / \bar{\rho}\right)^{2}+\left(\sigma_{T} / \bar{T}\right)^{2}\right]^{1 / 2}
\end{aligned}
where we use the averages as our best estimates of P, ρ, and T. This last result looks like eq. (A.14). In fact, we could have used eq. (A.14) directly and avoided all the calculus.
Thus, we would report our calculated pressure as:
\(\ P=\bar{P} \pm \sigma_{P}\)
A.4.4. Error Propagation
Error propagation tells us how the errors in A and B affect the error of D, where D depends on A and B according to some equation. Namely, how can we estimate σD knowing σA and σB ? Assume the errors in A and B are independent of each other.
For a simple sum or difference (e.g., D = A + B, or D = A – B), then
\begin{align}\sigma_{D}=\left[\sigma_{A}^{2}+\sigma_{B}^{2}\right]^{1 / 2}\tag{A.11}\end{align}
For D = c·A where c is a constant, then
\begin{align}\sigma_{D}=\mathbf{c} \cdot \sigma_{A}\tag{A.12}\end{align}
Similarly, if D = cA·A ± cB·B where cA and cB are different constants, then
\begin{align}\sigma_{D}=\left[c_{A}^{2} \cdot \sigma_{A}^{2}+c_{B}^{2} \cdot \sigma_{B}^{2}\right]^{1 / 2}\tag{A.13}\end{align}
For a simple product D = c·A·B or quotient D = c·A/B, then
\begin{align}\sigma_{D}=\bar{D} \cdot\left[\left(\sigma_{A} / \bar{A}\right)^{2}+\left(\sigma_{B} / \bar{B}\right)^{2}\right]^{1 / 2}\tag{A.14}\end{align}
where \(\overline{A}\) is the average of A, \(\overline{B}\) is the average of B, and \(\overline{D}\) is the average of D (i.e., \(\ \overline{D} =c\overline{A}\ \overline{B}, or \overline{D} = c \overline{A}\ / \overline{B}\)
For a simple power relationship D = c·Am where m is a fixed constant, then
\begin{align}\sigma_{D}=\bar{D} \cdot m \cdot\left(\sigma_{A} / \bar{A}\right)\tag{A.15}\end{align}
For the general case of a product of factors raised to various fixed (errorless) powers D = c·Am·Bq , then
\begin{align}\sigma_{D}=\bar{D} \cdot\left[m^{2} \cdot\left(\sigma_{A} / \bar{A}\right)^{2}+q^{2} \cdot\left(\sigma_{B} / \bar{B}\right)^{2}\right]^{1 / 2}\tag{A.16}\end{align}
For a logarithm such as D = ln(c·A), where c is a constant, then
\begin{align}\sigma_{D}=\left(\sigma_{A} / \bar{A}\right)\tag{A.17}\end{align}
For an exponential such as D = ec·A where c is a constant, then
\begin{align}\sigma_{D}=c \cdot \bar{D} \cdot \sigma_{A}\tag{A.18}\end{align}
For more complicated relationships, the rules above can be combined or used sequentially (or see the HIGHER MATH box).
Sample Application
Observations give P1 = 100 ± 0.1 kPa, P2 = 50 ± 0.5 kPa, and \(\ \overline{T_{v}}=260 \pm 5 \mathrm{K}\). Use hypsometric eq. to find ∆z.
Find the Answer
Given: \(\ \bar{P}_{1}=100 \mathrm{kPa}, \sigma_{P 1}=0.1 \mathrm{kPa}, \bar{P}_{2}=50 \mathrm{kPa}\)
\(\ \bar{P}_{1}=100 \mathrm{kPa}, \sigma_{P 1}=0.1 \mathrm{kPa}, \bar{P}_{2}=50 \mathrm{kPa},
\sigma_{P 2}=0.5 \mathrm{kPa}, \overline{T_{v}}=260 \mathrm{K}, \sigma_{T}=5 \mathrm{K}\)
Hyp. eq.(1.26a): \(\ \Delta z=a \cdot \overline{T_{v}} \cdot \ln \left(P_{1} / P_{2}\right), a=29.3 \mathrm{m} \mathrm{K}^{-1}\)
Find: ∆z = ? ± ? m. Namely, find \(\ \overline{\Delta z}\) = ?m, σ∆Z = ? m
Method: Use error propagation rules sequentially.
For (P1/P2): Average(P/P) = (100kPa)/(50kPa) = 2
Use eq. (A.14): σP/P = 2·[(0.1/100)2 + (0.5/50)2] 1/2 = 0.02
For a·ln(P1/P2): Average =(29.3m K–1)·ln(2) = 20.31 m K–1
Use eq. (A.17): σa·ln =(29.3m K–1)·(0.02/2) = 0.293 m K–1
For \(\ \overline{T_{v}} \cdot a \cdot \ln \left(P_{1} / P_{2}\right): \text { Average}=\left(20.31 \mathrm{m} \mathrm{K}^{-1}\right) \cdot(260 \mathrm{K})=\underline{\bf{5281 \mathrm{m}}}\)
Use eq. (A.14): σ∆Z=(5281m)·[(5/260)2+(0.293/20.31)2] 1/2 = 127 m
Exposition: Notice that error-propagation eqs. (A.11 - A.18) are dimensionally consistent. A good check.
A.5. A SCIENTIFIC PERSPECTIVE
Science is a philosophy. It is faith in a set of principles that guide the actions of scientists. It is a faith based on observation. Scientists try to explain what they observe. Theories not verified by observations are discarded. This philosophy applies to atmospheric science, also known as meteorology.
A good theory is one that works anywhere, anytime. Such a theory is said to be universal. Engineers utilize universal theories with the expectation they will continue working in the future. The structures, machines, circuits, and chemicals designed by engineers that we use in every-day life are evidence of the success of this philosophy.
But we scientists and engineers are people, and share the same virtues and foibles as others. Those of you planning to become scientists or engineers might appreciate learning some of the pitfalls so that you can avoid them, and learning some of the tools so that you can use them to good advantage.
For this reason, scattered throughout the book are boxes called “A SCIENTIFIC PERSPECTIVE”, summarized in Table A–5. These go beyond the mathematical preciseness and objective coldness that is the stereotype of scientists. These boxes cover issues and ideas that form the fabric of the philosophy of science. As such, many are subjective. While they give you one scientist’s (my) perspectives, I encourage you to discuss and debate these issues with other scientists, colleagues, and teachers.
The best scientists and engineers need more than the good habits of diligence and meticulousness. They need passion for their field, and they need creativity. In this regard, they are kindred spirits to artists, composers, musicians, authors, and poets.
While an observation is something that can usually be quantified, the explanation or theory for it comes from the minds of people. For example, does light consist of particles (photons) or waves? Probably it consists of neither, but those are two theories from the creative imagination of scientists that have proved useful in explaining the observations.
The joy that a scientist feels after successfully explaining an observation, and pride that an engineer feels for making something work within the constraints of physics and economics, are no less intense than the joy and pride felt by an artist who has just completed his or her masterpiece.
Approach your work with passion, evaluate your result objectively, and enjoy your travel through life as you help society.
| Table A-5. Guidelines & issues for scientists. Chapters & topics of the “A SCIENTIFIC PERSPECTIVE” boxes. | ||
| Chapter | Issues | Page |
|---|---|---|
| 1 | Descartes and the Scientific Method | 2 |
| 1 | Check for Errors | 16 |
| 1 | Be Meticulous | 20 |
| 1 | Give Credit | 24 |
| 2 | Scientific Laws — The Myth | 38 |
| 2 | Seek Solutions | 46 |
| 3 | Expert vs. Novice | 72 |
| 4 | Look for Patterns | 107 |
| 6 | Cargo Cult Science | 167 |
| 7 | Consequences | 218 |
| 9 | Creativity in Engineering | 288 |
| 10 | Be Creative | 293 |
| 11 | Toy Models | 330 |
| 11 | Residuals | 340 |
| 11 | The Scientific Method Revisited | 343 |
| 11 | Model Sensitivity | 350 |
| 12 | Math Clarity | 393 |
| 13 | Truth vs. Uncertainty | 470 |
| 14 | Be Safe (many parts) | 485, 517 |
| 15 | Be Safe (continuation) | 567, 583, 584 |
| 17 | Simple is Best | 680 |
| 18 | Parameterization Rules | 715 |
| 19 | Data Misinterpretation | 729 |
| 19 | The Citizen Scientist | 738 |
| 20 | Mathematics | 762 |
| 20 | Scientific Revolutions | 773 |
| 21 | Ethics and Data Abuse | 826 |
| 22 | Great Scientists Make Big Mistakes Too | 863 |
| A | Problem Solving | 869 |
| A | Have Passion | 877 |
A.6. REVIEW
SI units are used by atmospheric scientists. Functional relationships between variables can sometimes be discerned when the data is plotted on linear, semi-log, or log-log graphs. An organized approach to problem solving that includes consideration of error propagation is recommended. The philosophy of science blends the passions of people with the objective analysis of observations. These principles are used throughout this book.
A.7. HOMEWORK EXERCISES
A.7.1. Broaden Knowledge & Comprehension
B1. Search the web for recommended units to use in meteorology, and list 3 that were not given in this chapter. [Hint, on the American Meteorological Society web site, search for a “Guide for Authors”.]
B2. For 5 of the universal constants listed in Appendix B, search the web to find their precision (i.e., the ± σ value). [Hint: try NIST (U.S. National Institute of Standards and Technology.]
A.7.2. Apply
A1. Convert the values on the left to the units at right, using a table of conversions.
| a. 50 miles =? km | b. 15 knots = ? m s–1 |
| c. 30 lb in–2 =? kPa | d. 5000 kW =? horsepower |
| e. 150 lbMass =? kg | f. 150 lbForce =? N |
| g. 12 ft = ? m | h. 50 km h–1 = ? m s–1 |
A2. Solve the expression on the left, and give the answer in the units at right, using a table of conversions, and the basic definitions of units:
- (55. knots) x (36. inches) =? m2·s–1
- (14. lbF in–2) x (2.5 m)2 = ? N
- (120. lbM) x (3. knots) / day =? mN
- (15. in Hg) x (2. ft3) = ? J
- (500. mb) x (3. knots) x (5. in)2 =? kW
- (9.8 m·s–2) x (6 kg) / (ft2) = ? mb
- (4200 J·kg–1·K–1) x (5°C) x (3.3 g) = ? ergs
- (2 ha)1/2 / 3 weeks = ? m s–1
A3. Find ∆T/∆z between the height at assigned letter (a - e) and the height immediately above it?
| z(m) | T(°C) | |
| 1000 | 10 | |
| e. | 500 | 15 |
| d. | 200 | 17 |
| c. | 100 | 17 |
| b. | 50 | 15 |
| a. | 0 | 10 |
A4. Convert the following temperatures:
| a. 15°C = ? K | b. 50°F = ? °C | c. 70 °F =? K |
| d. 48°C = ? °F | e. 400 K = ? °F | f. 250 K=?°C |
A5(§). Plot the following relationships on linear, semi-log, and log-log graphs. Use a spreadsheet (§) on a personal computer to make this easier. Any variable with subscript “o” represents a constant.
| a. I = Io · (Ro/R)2 | b. U = Uo · ln(z/zo) |
| c. E = Eo · exp(–z/zo) | d. f = co / λ |
| e. q = e / eo | f. c = co · exp[– (z/zo)2] |
| g. w = [2·(F/m)o·z] 1/2 | h. ∆P/∆Po = (1/5)·(R/Ro]4 |
A6. Given: A = 4000±20 m, B = 300±5 K, C = 80±2 m Also, k = 5 is a constant. Find \(\ D=\bar{D} \pm \sigma_{D}\) for:
| a. D = A + C | b. D = A – C | c. D = 3C + A |
| d. D = k·B | e. D = k2·A | f. D = A/B |
| g. D = A·C | h. D = A·B/C | i. D = (C+A)/B |
| j. D = Ak | k. D = B–k | m. D = Ck·B1/3 |
| n. D = k·ln(A/25m) | o. D = k·(C–A)/ln(B/273K) |
A.7.3. Evaluate & Analyze
E1. Is anything dimensionally wrong with the following equations, given: P = 100 kPa, z = 2 km, T = 30°C, W = 0.5 m s–1? If so, why?
| a. log(P) = z | b. sin(T) = W |
| c. arccos(P) = T | d. exp(–P/z) = 1 |
| e. cos(W) = 2 | f. ln(0) = z |
| g. ln(–10) = T | h. exp(0) = 1 |
E2. What is the difference between a good assumption and a bad one? What can you do to detect bad assumptions?
A.7.4. Synthesize
S1. Suppose that you discovered a new physical characteristic of nature, and that you devised a new dimension to explain it. However, also assume that the list of basic dimensions in Table A–1 is still valid, which means that your new dimension must be able to be described in terms of the basic dimensions. Describe the steps that you could take to determine the relationship between your new physical dimension and the basic units.
S2. Suppose science did not involve human creativity. What physical “laws” might have been described differently than they are now, or might have not been discovered at all?


