9.2: Synoptic Weather Maps
- Page ID
- 9584
Weather observations that were taken synoptically (i.e., simultaneously) at many weather stations worldwide can be drawn on a weather map. For any one station, the weather observations include many different variables. So a shorthand notation called a station-plot model was devised to use symbols or glyphs for each weather element, and to write those data around a small circle representing the station location.
But the raw numbers and glyphs plotted on a map at hundreds of stations can be overwhelming. So computers or people can analyze the map to create a coherent picture that integrates together all the weather elements, such as in Fig. 9.13.
Three steps are needed to create such maps. First, the weather data must be observed and communicated to central locations. Second, the data is tested for quality, where erroneous or suspect values are removed. These steps were already discussed.
Third, the data is analyzed, which means it is integrated into a coherent picture of the weather. This last step often involves interpolation to a grid (if it is to be analyzed by computers), or drawing of isopleths and identification of weather features (lows, fronts, etc.) if used by humans.
[Based on original analyses by Jon Martin.]
The resulting synoptic-weather map shows scales of weather (see table in the Forces & Winds chapter) that are called synoptic-scale. The field of study of these weather features (fronts, highs, lows, etc.) is called synoptics, and the people who study and forecast these features are synopticians.
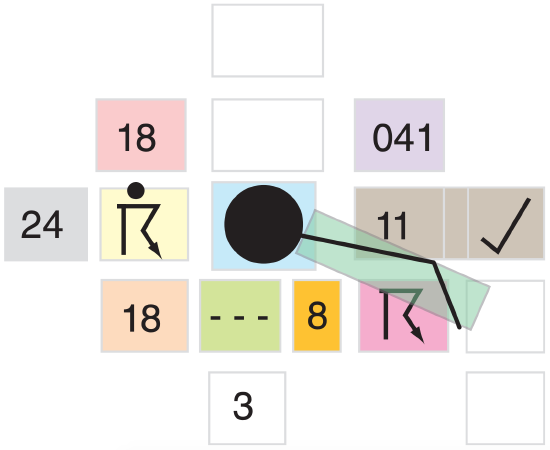
9.3.1. Station Plot Model
On weather maps, the location of each weather station is circled, and that station’s weather data is plotted in and around the circle. The standardized arrangement of these data in a grid is called a station plot model (Fig. 9.14). Before the days of computerized geographic information systems (GIS), meteorologists had to rely on abbreviated codes to pack as much data around each plotted weather station as possible. These codes are still used today.
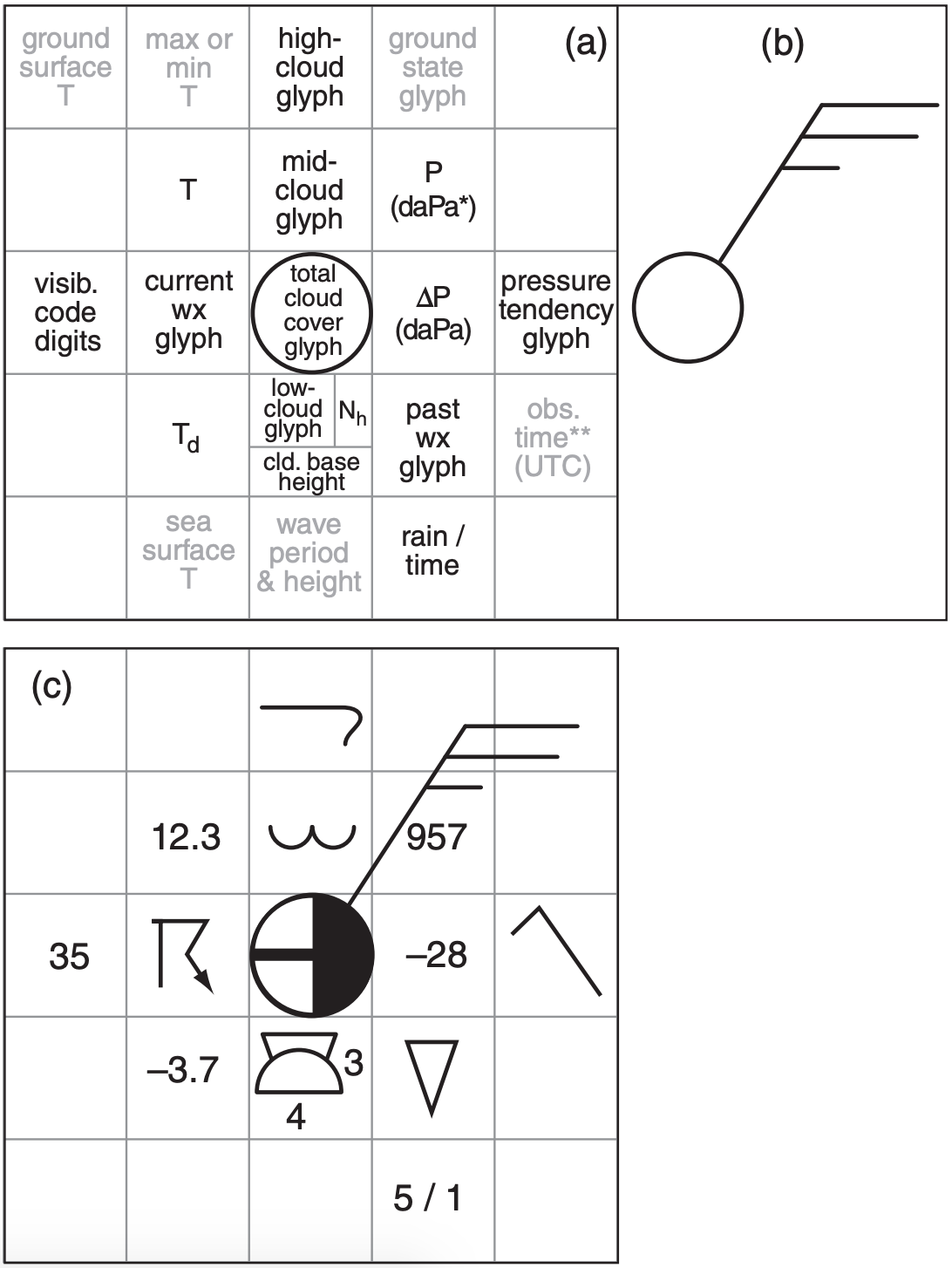
Unfortunately, different weather organizations/ countries use different station plot models and different codes. Here is how you interpret the surface station plot models for the World Meteorological Organization (WMO) and USA. Canada uses WMO. See WMO-No. 485 Appendix II-4 for details.
- T is a two-digit temperature in whole degrees (°C in most of the world; °F if plotted by the USA). WMO allows 3 digits plus decimal point and sign, where tenths of degrees is after the decimal point.
Example: 12 means 12°F in the USA. 12.3 means 12.3°C for WMO.
[CAUTION: On weather maps produced in the USA, temperatures at Canadian weather stations are often converted to °F before being plotted. The opposite happens for USA stations plotted on Canadian weather maps — they are first converted to °C. You should always think about the temperature value to see if it is reasonable for the units you assume.]
- Td is a two-digit dew-point temperature in whole degrees (°C in most of the world; °F if plotted by the USA). WMO allows 3 digits plus decimal point and sign when precision is to tenths of degrees.
Example: –4 means –4°F in the USA. –3.7 means –3.7°C for WMO. [Same CAUTION as for T.]
- P is the 3 least-significant digits of mean sea-level pressure in whole dekaPascals. To the left of the 3 digits, prefix either “9” or “10”, depending on which one gives a value closest to standard sea-level pressure. For kPa, insert a decimal point two places from the right. For hPa, insert a decimal point one place from the right.
Example: 041 means 10041 daPa = 1004.1 hPa = 1004.1 mb = 100.41 kPa. New example: 957 means 9957 daPa = 995.7 hPa = 995.7 mb = 99.57 kPa.
[CAUTION: Some organizations report P in inches of mercury (in. Hg.) instead of hPa. PMSL (in. Hg.) is an altimeter setting, used by aircraft pilots.]
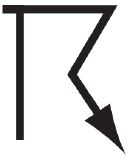
- Past wx is a glyph (Table 9-2) for past weather in the past hour (or past 6 hours for Canada). It is blank unless different from present weather.
Example:  means showers.
means showers.
- Current wx is a glyph for present weather (at time of the weather observation). Tables 9-3 show the commonly used weather glyphs.
Examples:  means snow shower;
means snow shower;  means thunderstorm with moderate rain.
means thunderstorm with moderate rain.
- Visib. is a 2-digit code for visibility (how far away you can see objects).
In the USA, visibility is in statute miles. (a) if visibility ≤ 3 1/8 miles, then vis can include a fraction.
(b) if 3 1/8 < visibility < 10 miles, then vis does not include a fraction.
(c) if 10 ≤ visibility, then vis is left blank.
Example: 2 1/4 means visibility is 2 1/4 statute miles. New example: 8 means visibility is 8 miles.
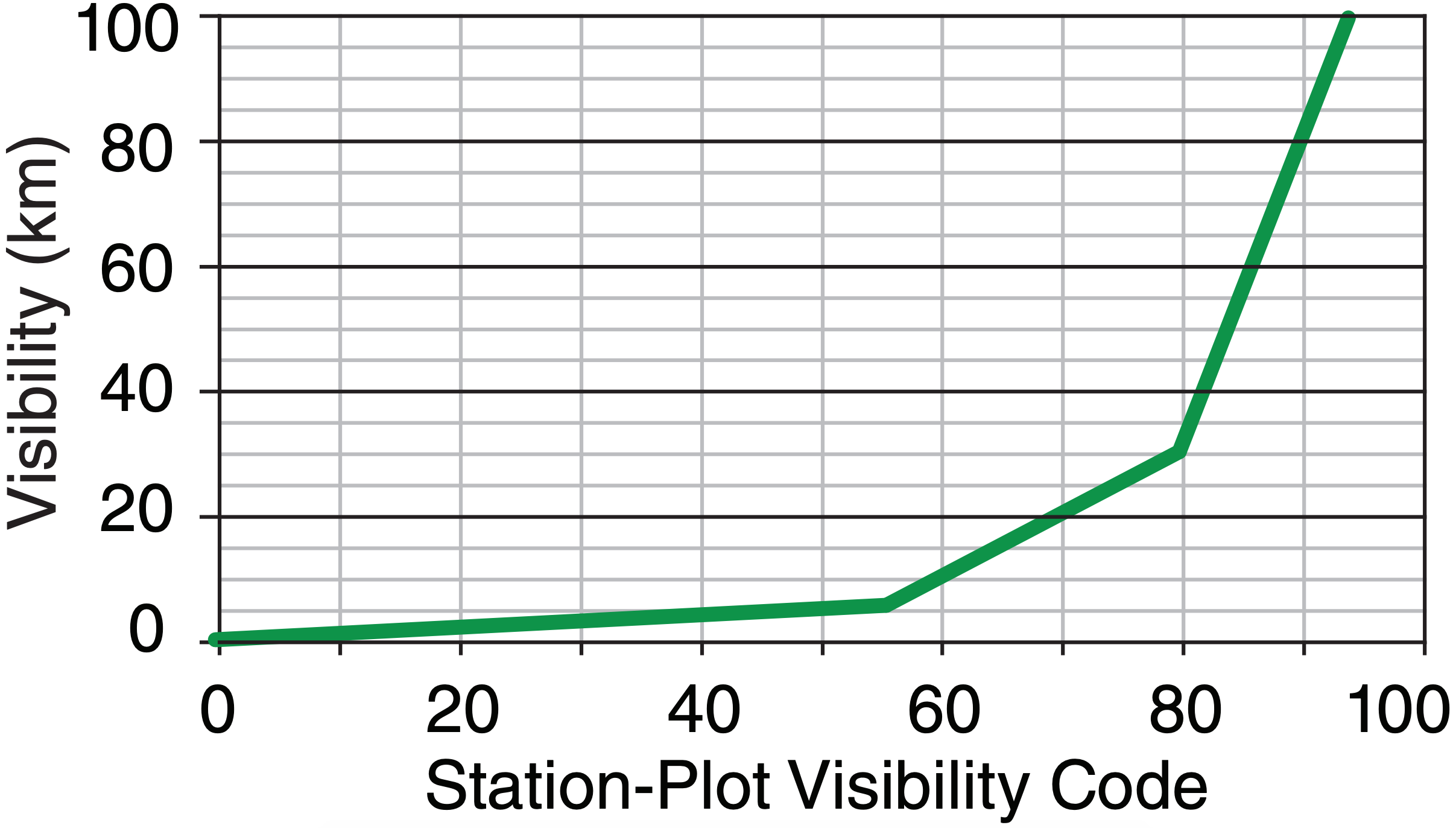
In Canada, visibility is in kilometers, but is coded into a two-digit vis code integer as follows:
(a) if vis ≤ 55, then visibility (km) = 0.1·vis
(b) if 56 ≤ vis ≤ 80, then visibility (km) ≈ vis – 50
(c) if 81 ≤ vis, then visibility (km) ≈ 5·(vis – 74)
Examples: 35 means 3.5 km. 66 means 16 km. 82 means 40 km. See Fig. 9.15 on page 278 for a graph.
| Table 9-2. WMO past or recent weather glyphs and codes (past wx). | ||
| Glyph | Meaning | METAR |
|---|---|---|
 |
Drizzle | DZ |
 |
Rain | RA |
 |
Snow | SN |
 |
Shower(s) | SH |
 |
Thunderstorm (thunder is heard or lightning detected, even if no precipitation) | TS |
 |
Fog (with visibility < 5/8 statute mile) | FG |
 |
Sand Storm | SS |
| Dust Storm | DS | |
 |
Drifting snow | DRSN |
| Blowing snow | BLSN | |
| Table 9-3a. Basic weather (wx) symbols and codes. | ||
| Glyph | Meaning | METAR |
|---|---|---|
| Precipitation: | ||
 |
Drizzle ‡ | DZ |
 |
Rain ‡ | RA |
 |
Snow ‡ | SN |
 |
Hail (large, diameter ≥ 5 mm) | GR |
 |
Graupel (snow pellets, small hail, size < 5 mm | GS |
 |
Ice Pellets (frozen rain, called sleet in USA) | PL |
 |
Ice Crystals (“diamond dust”) | IC |
 |
Snow Grain | SG |
 |
Ice Needles | |
| Unknown Precipitation (as from automated station) | UP | |
| Obscuration: | ||
 |
Fog (with visibility < 5/8 statute mile) ‡ | FG |
 |
Mist (diffuse fog, with visibility ≥ 5/8 statute mile) | BR |
 |
Haze | HZ |
 |
Smoke | FU |
| Volcanic Ash | VA | |
 |
Sand in air | SA |
| Dust in air | DU | |
| Spray | PY | |
| Storms & Misc.: | ||
 |
Squall | SQ |
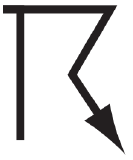 |
Thunderstorm (thunder is heard or lightning detected, even if no precipitation)‡ | TS |
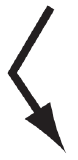 |
Lightning | |
 |
Funnel Cloud | FC |
| Tornado or Waterspout | +FC | |
 |
Dust Devil (well developed) | PO |
 |
Sand Storm | SS |
| Dust Storm | DS | |
| ‡ Can be used as a “Past Weather” glyph | ||
| Table 9-3b. Weather-code modifiers | ||
| Glyph | Meaning | METAR prefix |
|---|---|---|
|
Intensity, Proximity, or Recency: (Grey box |
||
 |
Light | – |
 |
Moderate | (blank) |
 |
Heavy | + |
 |
Intermittent and light ; moderate ; heavy | (no code for intermittent) |
 |
In the vicinity. In sight, but not at the weather stn. | VC |
 |
Virga (precip. in sight, but not reaching the ground). | VIRGA |
 |
In past hour, but not now | |
 |
Increased during past hour, and occurring now | |
 |
Decreased during the past hour, and occurring now | |
| Descriptor: | ||
 |
Shower (slight) | –SH |
 |
Shower (moderate) | SH |
| Shower (heavy) | +SH | |
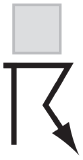 |
Thunderstorm | TS |
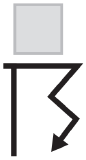 |
Thunderstorm (heavy) | +TS |
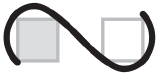 |
Freezing. (if light, use left placeholder only) *** | FZ |
 |
Blowing (slight)** | –BL |
| Blowing (moderate)** | BL | |
 |
Blowing (strong, severe)** | +BL |
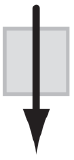 |
Drifting (low) (For DU, SA, SN raised < 2 m agl) | DR |
 |
Shallow* | MI |
| Partial* | PR | |
| Patchy* | BC | |
| ( * Prefixes for fog FG only.) ( ** Prefixes only for DU, SA, SN or PY.) ( *** Prefixes only for FG, DZ, or RN.) | ||
| Table 9-4. High clouds (WMO). | |
| Glyph | Meaning |
|---|---|
 |
Cirrus (scattered filaments, “mares tails”, not increasing). |
 |
Cirrus (dense patches or twisted sheaves of filament bundles). |
 |
Cirrus (dense remains of a thunderstorm anvil). |
 |
Cirrus (hook shaped, thickening or spreading to cover more sky). |
 |
Cirrus and cirrostratus increasing coverage or thickness, but covering less than half the sky. |
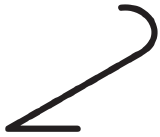 |
Cirrus and cirrostratus covering most of sky, and increasing coverage or thickness. |
 |
Cirrostratus veil covering entire sky. |
 |
Cirrostratus, not covering entire sky. |
 |
Cirrocumulus (with or without smaller amounts of cirrus and/or cirrostratus). |
| Table 9-5. Mid-level clouds (WMO). | |
| Glyph | Meaning |
|---|---|
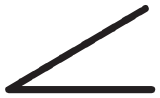 |
Altostratus (thin, semitransparent). |
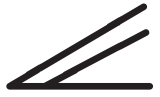 |
Altostratus (thick), or nimbostratus. |
 |
Altocumulus (thin). |
 |
Altocumulus (thin, patchy, changing, and/or multi-level). |
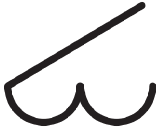 |
Altocumulus (thin but multiple bands or spreading or thickening). |
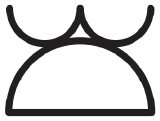 |
Altocumulus (formed by spreading of cumulus). |
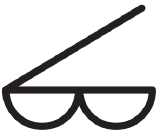 |
Multiple layers of middle clouds (could include altocumulus, altostratus, and/or nimbostratus). |
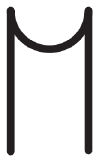 |
Altocumulus castellanus (has turrets or tufts). |
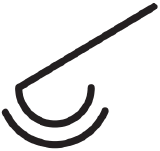 |
Altocumulus of chaotic sky (could include multi-levels and dense cirrus). |
| Table 9-6. Low clouds (WMO). | |
| Glyph | Meaning |
|---|---|
 |
Cumulus (Cu) humilis. Fair-weather cumulus. Little vertical development. |
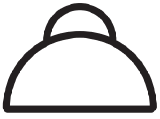 |
Cumulus mediocris. Moderate to considerable vertical development. |
 |
Cumulus congestus. Towering cumulus. No anvil top. |
 |
Stratocumulus formed by the spreading out of cumulus. |
 |
Stratocumulus. (Not from spreading cu) |
 |
Stratus. |
 |
Scud. Fractostratus or fractocumulus, often caused by rain falling from above. |
 |
Cumulus and stratocumulus at different levels (not cause by spreading of Cu. |
 |
Cumulonimbus. Thunderstorm. Has anvil top that is glaciated (contains ice crystals, and looks fibrous). |
• High-cloud glyphs are shown in Table 9-4.
• Mid-cloud glyphs are shown in Table 9-5.
• Low-cloud glyphs are shown in Table 9-6.
• Nh is fraction of sky covered by low clouds. If no low clouds, then mid clouds. Units: oktas (eighths). This can differ from the total sky coverage (see Table 9-10), which is indicated by the shading inside the station circle. Example: 3 means 3/8 coverage.
• Cloud-base height above ground is for the lowest cloud seen. It is a single-digit code (see Table 9-7).
• ∆P is 2 digits giving pressure change in the past 3 hours, prefixed with + or –. Units are hundredths of kPa (or tenths of hPa). Example: –28 is a pressure decrease of 0.28 kPa or 2.8 hPa.
• Pressure tendency glyphs represent the pressure change (barometric tendency) during the past 3 hours (Table 9-8). It mimics the trace on a barograph.
| Table 9-7. Codes for cloud-base height (zc). | ||
| Code | meters agl | feet agl |
|---|---|---|
| 0 | 0 to 49 | 0 to 149 |
| 1 | 50 to 99 | 150 to 299 |
| 2 | 100 to 199 | 300 to 599 |
| 3 | 200 - 299 | 600 to 999 |
| 4 | 300 - 599 | 1,000 to 1,999 |
| 5 | 600 to 999 | 2,000 to 3,499 |
| 6 | 1,000 to 1,499 | 3,500 to 4,999 |
| 7 | 1,500 to 1,999 | 5,000 to 6,499 |
| 8 | 2,000 to 2,499 | 6,600 to 7,999 |
| 9 | ≥ 2,500 | ≥ 8,000 |
| Table 9-8. Symbols for pressure change (barometric tendency) during the past 3 hours. (a) | |
| Glyph | Meaning |
|---|---|
 |
Rising, then falling |
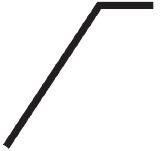 |
Rising, then steady or rising more slowly |
 |
Rising steadily or unsteadily |
 |
Falling or steady, later rising; or Rising slowly, later rising more quickly |
 |
Steady |
 |
Falling, then rising, but ending same or lower |
 |
Falling, then steady or falling more slowly |
 |
Falling steadily or unsteadily |
 |
Steady or rising, then falling; or Falling, then falling more quickly |
| Table 9-9. Interpretation of wind barbs. | ||
| Symbol | Wind Speed | Description |
|---|---|---|
 |
calm | two concentric circles |
 |
1 - 2 speed units | shaft with no barbs |
 |
5 speed units | a half barb (half line) |
 |
10 speed units | each full barb (full line) |
 |
50 speed units | each pennant (triangle) |
|
||
• ∆tR is a single-digit code that gives the number of hours ago that precipitation began or ended. The WMO station-plot model does not include ∆tR. But ∆tR is on some of the US station-plot models, to the right of the past-weather glyph. Here is the code:
0 means no precipitation
1 means 0 to 1 hour ago
2 means 1 to 2 hours ago
3 means 2 to 3 hours ago
4 means 3 to 4 hours ago
5 means 4 to 5 hours ago
6 means 5 to 6 hours ago
7 means 7 to 12 hours ago
8 means more than 8 hours ago
• Rain/time-code is the accumulated liquid-equivalent precipitation amount during a past time interval. The time interval is in units of 6 hours, so a time code of 1 means 6 hours; a time code of 2 means 12 hours. In the USA, the units are hundredths of inches per 6 hours (the time code is not included). For example: 45 means 0.45 inches in the US. In Canada, the units are mm — the WMO standard.
Example: 5/1 means 5 mm in the past 6 hours.
• Wind is plotted as a direction shaft with barbs to denote speed (Fig. 9.14b). Table 9-9, reproduced from the Forces & Winds chapter, explains how to interpret it.
Example: Fig. 9.14c shows 25 kt from the N.E.
• Total cloud cover is indicated by the portion of the station-plot circle that is blackened (Fig. 9.14b). Table 9-10, reproduced from the Cloud chapter, explains its interpretation. Example: 5/8 coverage in Fig. 9.14c.
| Table 9-10. Sky cover. Oktas=eighths of sky covered. | ||||
| Sky Cover (oktas) | Symbol | Name | Abbr. | Sky Cover (tenths) |
|---|---|---|---|---|
| 0 |  |
Sky Clear | SKC | 0 |
| 1 |  |
Few* Clouds | FEW* | 1 |
| 2 |  |
2 to 3 | ||
| 3 |  |
Scattered | SCT | 4 |
| 4 |  |
5 | ||
| 5 |  |
Broken | BKN | 6 |
| 6 |  |
7 to 8 | ||
| 7 |  |
9 | ||
| 8 |  |
Overcast | OVC | 10 |
| (9) |  |
Sky Obscured | unknown | |
| (/) |  |
Not Measured | unknown | |
* “Few” is used for (0 oktas) < coverage ≤ (2 oktas).
In the next subsection you will learn how to analyze a weather map. You can do a hand analysis (manual analysis) by focusing on just one meteorological variable. For example, if you want to analyze temperatures, then you should focus on just the temperature data from the station plot for each weather station, and ignore the other plotted data. This is illustrated in Fig. 9.16, where I have highlighted the temperatures to make them easier to see.
[CAUTION: Do not forget that the plotted temperature represents the temperature at the station location (namely, at the plotted station circle), not displaced from the station circle as defined by the station plot model.]
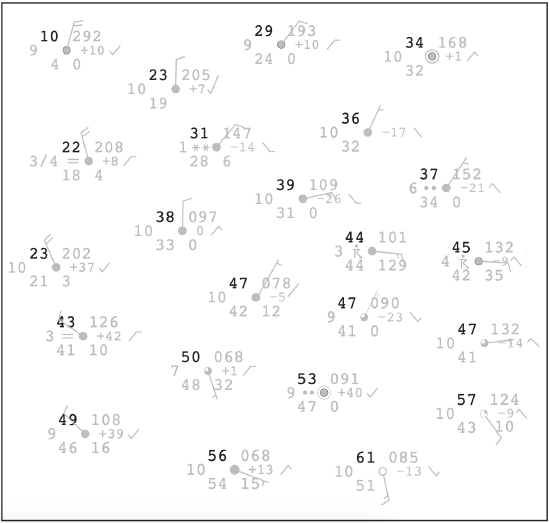
Sample Application
Decode the (a) station plot and the (b) METAR below, and compare the information they contain.
|
(a) Station Plot Example
|
(b) METAR METAR CYYB 040000Z 11010KT 1 1/2SM TSRA BR BKN008 OVC020 18/18 A2965 RMK SF5SC3 CB ASOCTD PRES UNSTDY SLP041 |
(c) Translation of METAR (Info from Stn Plot underlined)
Meteorological Aviation Report for North Bay (CYYB) ON, Canada on 4th day of the month at 0000 UTC. Wind from 110° true at 10 knots.
Visibility 1.5 statuate miles (= 2.4 km).
Present weather is thunderstorm with moderate rain and mist.
Cloud coverage: broken clouds with base at 800 feet above ground, overcast with base at 2000 feet.
Temperature is 18°C, and dew point is 18°C.
Altimeter is 29.65 inches of mercury.
Remarks:
Stratus fractus clouds with 5/8 coverage, and Stratocumulus clouds with 3/8 coverage, both associated with cumulonimbus.
Sea-level pressure is unsteady 100.41 kPa.
[Additional info in station plot, but not in METAR: past weather was thunderstorm; pressure first decreased, then increased with net increase of 0.11 kPa in 3 hr.]
9.3.2. Map Analysis, Plotting & Isoplething
You might find the amount of surface-observation data such as plotted in Fig. 9.16 to be overwhelming. To make the plotted data more comprehensible, you can simplify the weather map by drawing isopleths (lines of equal value, see Table 1-6).
For example, if you analyze temperatures, you draw isotherms on the weather map. Similarly, if you analyze pressures you draw the isobars, or for humidity you draw isohumes.
Also, you can identify features such as fronts and centers of low and high pressure. Heuristic models of these features allow you to anticipate their evolution (see chapters on Fronts & Airmasses and Extratropical Cyclones).
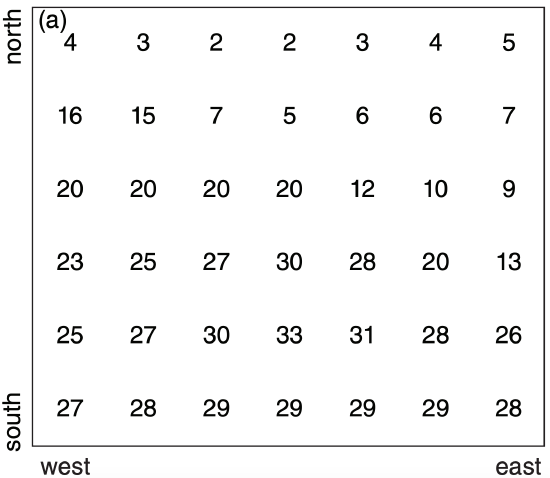

Most weather maps are analyzed by computer. Using temperature as an example, the synoptic temperature observations are interpolated by the computer from the irregular weather-station locations to a regular grid (Fig. 9.17a). Such a grid of numbers is called a field of data, and this particular example is a temperature field. A discrete temperature field such as stored in a computer array approximates the continuously-varying temperature field of the real atmosphere. The gridded field is called an analysis.
Regardless of whether you manually do a hand analysis on irregularly-spaced data (as in Fig. 9.16), or you let the computer do an objective analysis on a regularly-spaced grid of numbers (as in Fig. 9.17a), the next steps are the same for both methods.
Continuing with the temperature example of Fig. 9.17, draw isotherms connecting points of equal temperature (Fig. 9.17b). The following rules apply to any line connecting points of equal value (i.e., isopleths), not just to isotherms:
- draw isopleths at regular intervals (such as every 2°C or 5°C for isotherms)
- interpolate where necessary between locations (e.g., the 5°C isotherm must be equidistant between gridded observations of 4°C & 6°C)
- isopleths never cross other isopleths of the same variable (e.g., isotherms can’t cross other isotherms, but isotherms can cross isobars)
- isopleths never end in the middle of the map
- label each isopleth, either at the edges of the map (the only places where isopleths can end), or along closed-loop isopleths
- isopleths have no kinks, except sometimes at fronts or jets
Finally, label any relative maxima and minima, such as the warm and cold centers in Fig. 9.17b.
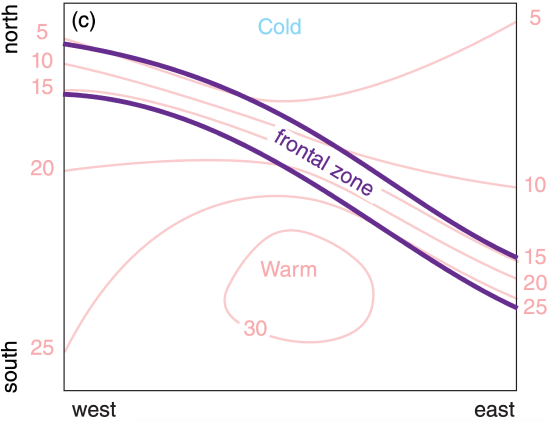
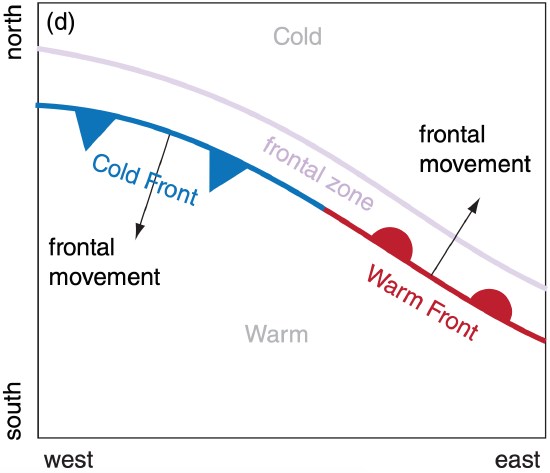
You can identify frontal zones as regions of tight isotherm packing (Fig. 9.17c), namely, where the isotherms are closer together. Note that no isotherm needs to remain within a frontal zone.
Finally, always draw a heavy line representing the front on the warm side of the frontal zone (Fig. 9.17d), regardless of whether it is a cold, warm, or stationary front.
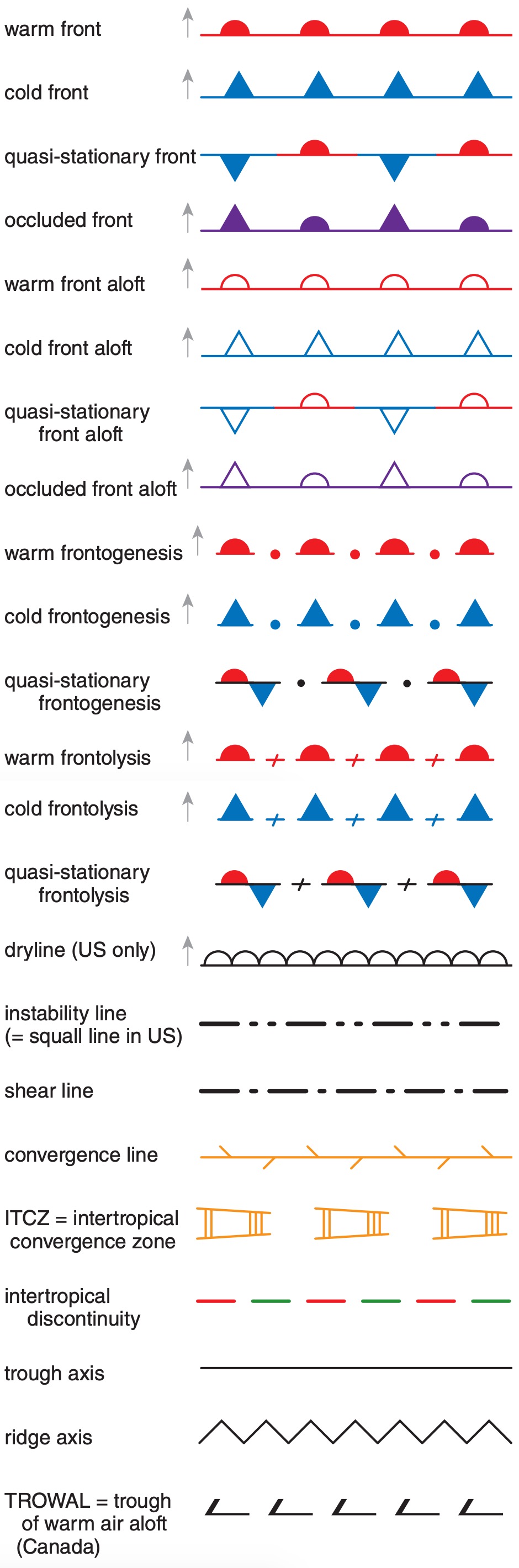
Frontal symbols are drawn on the side of the frontal line toward which the front moves. Draw semicircles to identify warm fronts (for cases where cold air retreats). Draw triangles to identify a cold front (where cold air advances). Draw alternating triangles and semicircles on opposite sides of the front to denote a stationary front, and on the same side for an occluded front. Fig. 9.18 summarizes frontal symbols, many of which will be discussed in more detail in the Airmasses and Fronts chapter.
In Fig. 9.17d, there would not have been enough information to determine if the cold air was advancing, retreating, or stationary, if I hadn’t added arrows showing frontal movement. When you analyze fronts on real weather maps, determine their movement from successive weather maps at different times, by the wind direction across the front, or by their position relative to low-pressure centers.
[sources: WMO-No.485 Manual on the Global Data Processing and Forecasting System (2010, 2012, 2015), page II-4-12; and WMO-No.306 Manual on Codes].



 is placeholder for a precipitation glyph from Table 9-3a. For example,
is placeholder for a precipitation glyph from Table 9-3a. For example,  means light drizzle.)
means light drizzle.) indicates a wind from the west at speed 75 units. Arrow tip is at the observation location.
indicates a wind from the west at speed 75 units. Arrow tip is at the observation location.