3.5: Heat Budget at a Fixed Location
- Page ID
- 9544
3.5.1. Eulerian Form of the First Law of Thermo
Picture a cube of air at a fixed location relative to the ground (i.e., an Eulerian framework). By being fixed, the cube experiences only small, slow changes in pressure. As a result, the pressure-change term in the First Law of Thermo (eq. 3.2d) can usually be neglected. What remains is an equation that says thermal energy transferred (∆q) per unit mass causes temperature change: ∆T = ∆q/Cp.
Dividing this equation by time interval ∆t gives a forecast equation for temperature: ∆T/∆t = (1/Cp)·∆q/ ∆t. A heat flux F (J m–2 s–1, or W m–2) into the volume could increase the temperature, but a heat flux out the other side could decrease the temperature. Thus, with both inflow and outflow of heat, net thermal energy will be transferred into the cube of air if the heat flux decreases with distance s across the cube: ∆q/∆t = –(1/ρ)·∆F/∆s. The inverse density factor appears because ∆q is energy per unit mass.
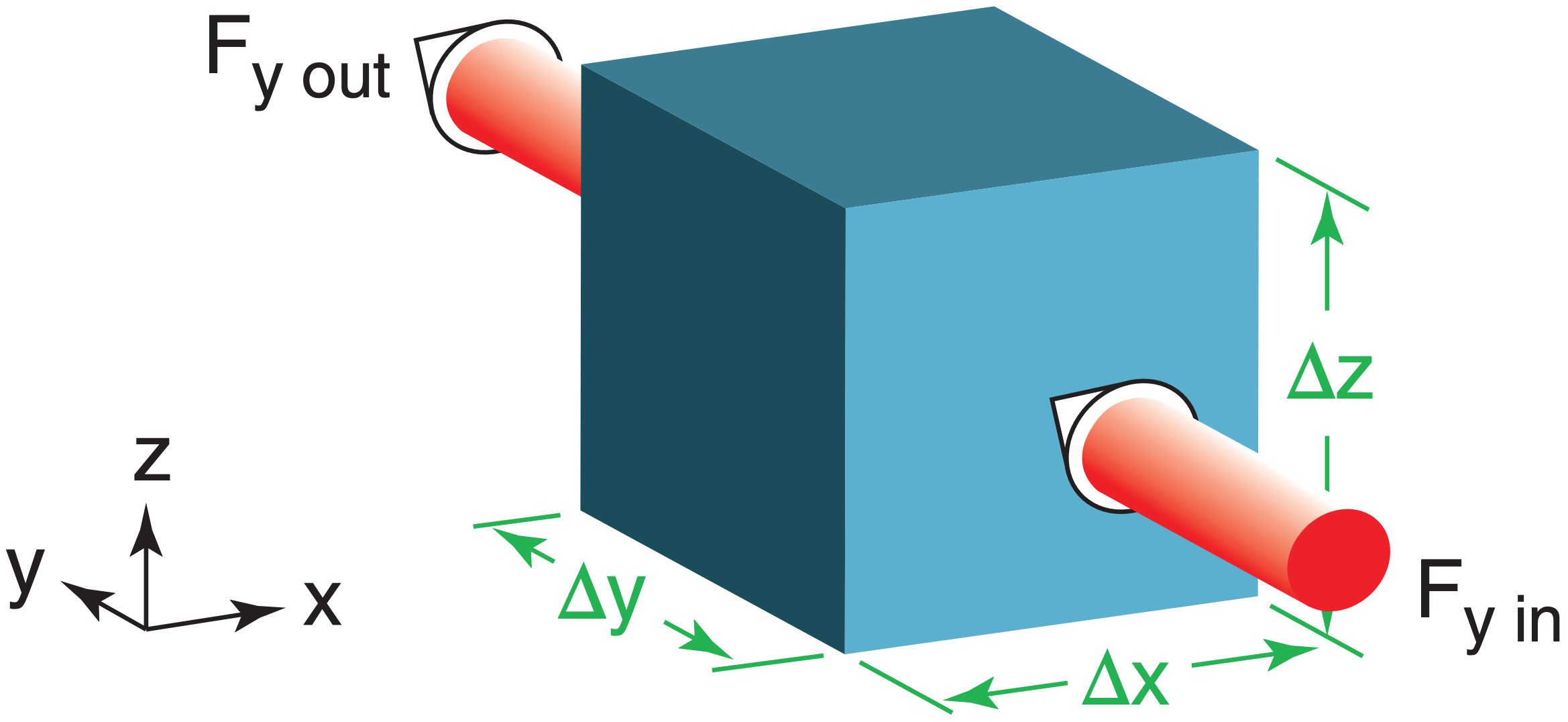
Heat flux convergence such as this causes warming, while heat flux divergence causes cooling. This flux gradient (change with flux across a distance) could happen in any of the three Cartesian directions. Thus, the temperature forecast equation becomes:
\(\ \begin{align} \frac{\Delta T}{\Delta t}=-\frac{1}{\rho \cdot C_{p}}\left[\frac{\Delta F_{x}}{\Delta x}+\frac{\Delta F_{y}}{\Delta y}+\frac{\Delta F_{z}}{\Delta z}\right]+\frac{\Delta S_{o}}{C_{p} \cdot \Delta t}\tag{3.16}\end{align}\)
where, for example, ∆Fy/∆y is the change in northward-moving flux Fy across a north-south distance ∆y (Figure 3.5). Additional heat sources can occur inside the cube at rate ∆So/∆t (J kg–1 s–1) such as when water vapor already inside the cube condenses into liquid and releases latent heat. The equation above is the Eulerian heat-budget equation, also sometimes called a heat conservation or heat balance equation.
Recall from Chapter 2 that we can define a kinematic flux by F = F/(ρ·Cp) in units of K m s–1 (equivalent to °C m s–1). Thus, eq. (3.16) becomes:
\(\ \begin{align} \frac{\Delta T}{\Delta t}=-\left[\frac{\Delta F_{x}}{\Delta x}+\frac{\Delta F_{y}}{\Delta y}+\frac{\Delta F_{z}}{\Delta z}\right]+\frac{\Delta S_{o}}{C_{p} \cdot \Delta t}\tag{3.17}\end{align}\)
We can also reframe this heat budget in terms of potential temperature, because with no movement of the cube of air itself, then ∆T = ∆θ.
\(\ \begin{align} \frac{\Delta \theta}{\Delta t}=-\left[\frac{\Delta F_{x}}{\Delta x}+\frac{\Delta F_{y}}{\Delta y}+\frac{\Delta F_{z}}{\Delta z}\right]+\frac{\Delta S_{0}}{C_{p} \cdot \Delta t}\tag{3.18}\end{align}\)
You may have wondered why, in the previous figure, a ∆Fy/∆y was negative, even though heat was deposited into the cube. The reason is that for gradients, the difference-direction of the denominator must be the same direction as the numerator; e.g.:
\(\ \begin{align}\frac{\Delta F_{y}}{\Delta y}=\frac{F_{y \ n o r t h s i d e}-F_{y\ \text {southside}}}{y_{\text {northside}}-y_{\text {southside}}}\end{align}\)
Similar care must be taken for gradients in the x and z directions.
Not only do we need to consider fluxes in each direction in eqs. (3.16 to 3.18), but for any one direction there might be more than one physical process causing fluxes. The other processes that we will discuss next are conduction (cond), advection (adv), radiation (rad), and turbulence (turb):
\(\ \begin{align}\frac{\Delta F_{x}}{\Delta x}=\left.\frac{\Delta F_{x}}{\Delta x}\right|_{a d v}+\left.\frac{\Delta F_{x}}{\Delta x}\right|_{c o n d}+\left.\frac{\Delta F_{x}}{\Delta x}\right|_{t u r b}+\left.\frac{\Delta F_{x}}{\Delta x}\right|_{r a d}\tag{3.20}\end{align}\)
\(\ \begin{align}\frac{\Delta F_{y}}{\Delta y}=\left.\frac{\Delta F_{y}}{\Delta y}\right|_{a d v}+\left.\frac{\Delta F_{y}}{\Delta y}\right|_{\text {cond}}+\left.\frac{\Delta F_{y}}{\Delta y}\right|_{\text {turb}}+\left.\frac{\Delta F_{y}}{\Delta y}\right|_{r a d}\tag{3.21}\end{align}\)
\(\ \begin{align}\frac{\Delta F_{z}}{\Delta z}=\left.\frac{\Delta F_{z}}{\Delta z}\right|_{a d v}+\left.\frac{\Delta F_{z}}{\Delta z}\right|_{\text {cond}}+\left.\frac{\Delta F_{z}}{\Delta z}\right|_{\text {turb}}+\left.\frac{\Delta F_{z}}{\Delta z}\right|_{\text {rad}}\tag{3.22}\end{align}\)
In addition to describing these fluxes, we will estimate typical contributions of latent heating as a body source (∆So), allowing us to simplify the full heat budget equation in an Eulerian framework.
Sample Application
In the figure below, suppose that the incoming heat flux from the south is 5 W m–2, and the outgoing on the north face of the cube is 7 W m–2. (a) Convert these fluxes to kinematic units. (b) What is the value of the kinematic flux gradient? (c) Calculate the warming rate of air in the cube, assuming the cube has zero humidity and is at a fixed altitude where air density is 1 kg m–3. The cube of air is 10 m on each side.
Find the Answer
Given: Fy in= 5 W·m–2 , Fy out = 7 W·m–2, ∆y = 10 m ρ = 1.0 kg m–3 ,
Find: a) Fx right = ? K·m s–1, Fx left = ? K·m s–1
b) ∆Fy/∆y = ? c) ∆T/∆t = ? K s–1
From Appendix B: Cp = 1004 J·kg–1·K–1
Also, don’t forget that 1 W = 1 J s–1 .
Diagram:
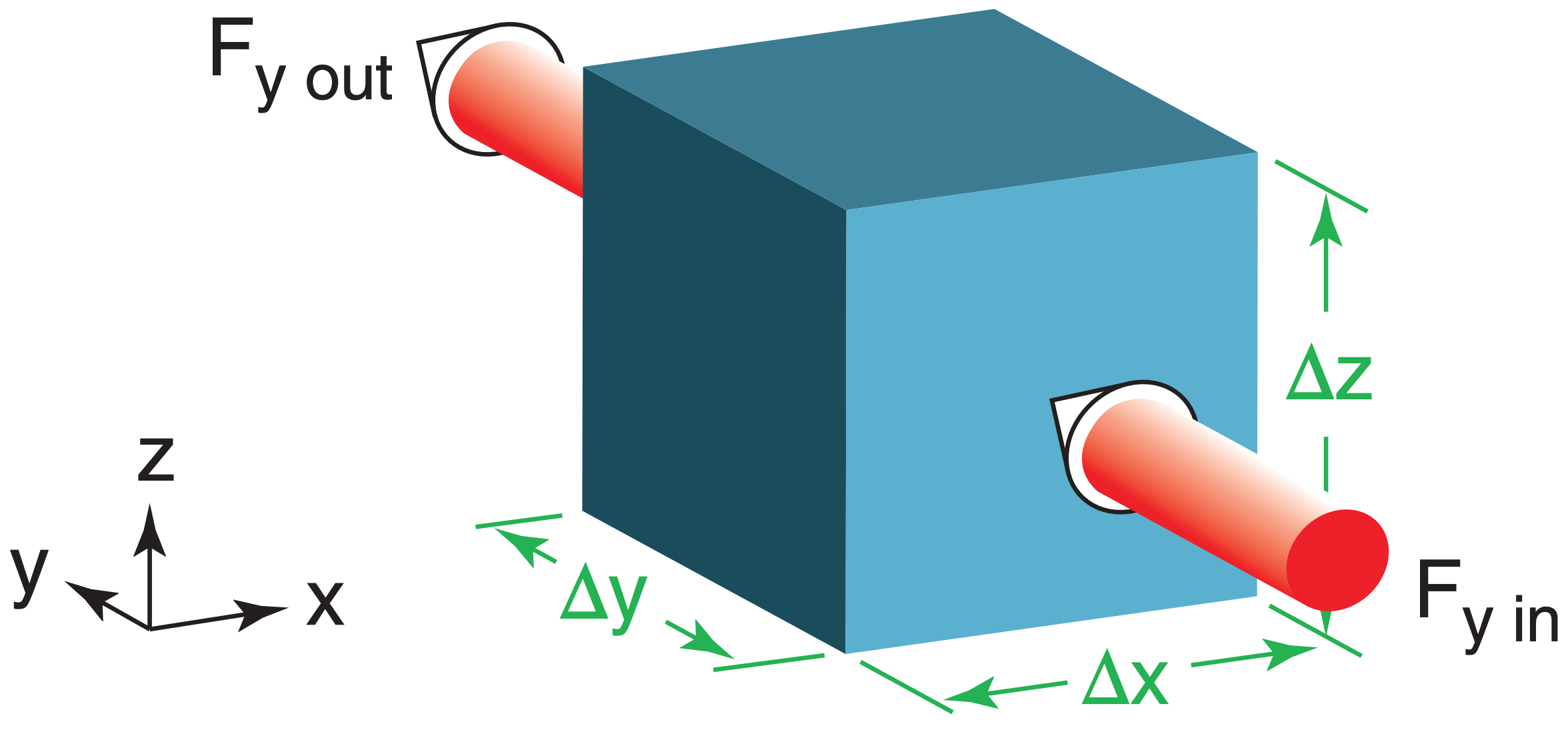
a) Apply eq. (2.11): F = F / (ρ·Cp)
Fy in = (5 J·s–1·m–2) / [ (1 kg m–3) · (1004 J·kg–1·K–1) )] = 4.98x10–3 K·m·s–1 .
Fy out = (7 W·m–2) / [ (1 kg m–3) · (1004 J·kg–1·K–1) )] = 6.97x10–3 K·m·s–1 .
b) Recall from Chapter 1 that the direction of y is such that y increases toward the north. If we pick the south side as the origin of our coordinate system, then ysouthside = 0 and ynorth-side = 10 m. Thus, the kinematic flux gradient (eq. 3.19) is
\(\frac{\Delta F_{y}}{\Delta y}=\frac{\left[\left(6.97 \times 10^{-3}\right)-\left(4.98 \times 10^{-3}\right)\right]\left(\mathrm{K} \cdot \mathrm{m} \cdot \mathrm{s}^{-1}\right)}{[10-0](\mathrm{m})}
=1.99 \times 10^{-4} \mathrm{K} \cdot \mathrm{s}^{-1}\)
Putting this into eq. (3.21) and then that eq. into eq. (3.17) yields: ∆T/∆t = – 1.99x10–4 K·s–1.
Check: Physics & units are reasonable.
Exposition: The cube does not get warmer, it gets colder at a rate of about 0.72°C/hour. The reason is that more heat is leaving than entering, which gave a positive value for the flux gradient.
What happens if either of the two fluxes are negative? That means that heat is flowing from north to south. So the sign is critical in helping us determine the movement and convergence of heat.
3.5.2. Advection of Heat
The AMS Glossary of Meteorology (2000) defines advection as transport of an atmospheric property by the mass motion of the air (i.e., by the wind). Temperature advection transports heat. Faster winds blowing hotter air causes greater advective heat flux:
\(\ \begin{align}F_{x\ adv}=U \cdot T\tag{3.23}\end{align}\)
\(\ \begin{align}F_{y\ adv}=V \cdot T\tag{3.24}\end{align}\)
\(\ \begin{align}F_{z\ a d v}=W \cdot T\tag{3.25}\end{align}\)
Updrafts also cause heat transport, where buoyant updrafts are called convection while non-buoyant updrafts are called advection.
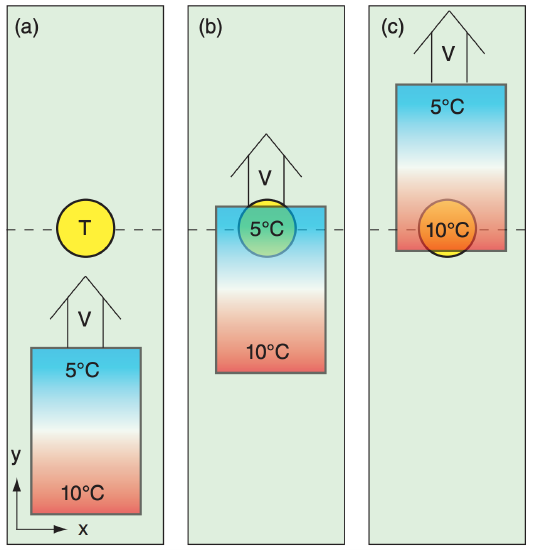
To illustrate temperature advection, consider a rectangular air parcel that is colder in the north and warmer in the south (Figure 3.6). Namely, the temperature gradient ∆T/∆y = negative in this example. A south wind (V = positive) blows the air north toward a thermometer mounted on a stationary weather station. First the cold air reaches the thermometer (Figure 3.6b). Later, the warm air blows over the thermometer (Figure 3.6c). So the thermometer experiences warming with time (∆T/∆t = positive) due to advection. Thus, it is not the advective flux Fx adv, but the gradient of advective flux (∆Fx adv/∆y) that causes a temperature change.
Although Figure 3.6 illustrates only horizontal advection in one direction, we need to consider advective effects in all directions, including vertical. For a mean wind with nearly uniform speed:
\(\ \begin{align}\frac{\Delta F_{x\ a d v}}{\Delta x}=\frac{U \cdot\left(T_{\text {east}}-T_{\text {west}}\right)}{x_{\text {east}}-x_{\text {west}}}=U \cdot \frac{\Delta T}{\Delta x}\tag{3.26}\end{align}\)
\(\ \begin{align} \frac{\Delta F_{y\ a d v}}{\Delta y}=\frac{V \cdot\left(T_{\text {north}}-T_{\text {south}}\right)}{y_{\text {north}}-y_{\text {south}}}=V \cdot \frac{\Delta T}{\Delta y}\tag{3.27}\end{align}\)
\(\ \begin{align}\frac{\Delta F_{z\ a d v}}{\Delta z}=W \cdot\left[\frac{\Delta T}{\Delta z}+\Gamma_{d}\right]\tag{3.28}\end{align}\)
Rising air cools at the dry adiabatic lapse rate of Γd = 9.8 °C km–1 . Since temperature of a rising air parcel is not conserved, this lapse-rate term must be added to the temperature gradient in the vertical advection equation. This same factor (with no sign changes) works for descending air too.
We can combine eqs. (3.26 - 3.28) with eq. (3.11) to express advection in terms of potential temperature θ:
\(\ \begin{align}\frac{\Delta F_{x\ a d v}}{\Delta x}=U \cdot \frac{\Delta \theta}{\Delta x}\tag{3.29}\end{align}\)
\(\ \begin{align}\frac{\Delta F_{y\ a d v}}{\Delta y}=V \cdot \frac{\Delta \theta}{\Delta y}\tag{3.30}\end{align}\)
\(\ \begin{align}\frac{\Delta F_{z\ a d v}}{\Delta z}=W \cdot \frac{\Delta \theta}{\Delta z}\tag{3.31}\end{align}\)
Sample Application
The cube of air from Figure 3.5 has T = 12°C along its south side, but smoothly increases in temperature to 15°C on the north side. This 100 km square cube is advecting toward the north at 25 km/hour. What warming rate at a fixed thermometer can be attributed to temperature advection?
Find the Answer
Given: V = 25 km h–1, ∆T = 15 – 12°C = 3°C, ∆y = 100 km
Find: ∆T/∆t = ? °C h–1 due to advection
Apply eq. (3.27) in eq. (3.21), and apply that in eq. (3.17); namely, ∆T/∆t = – V · (∆T/∆y) = – (25 km h–1) · [ 3°C / 100 km] = – 0.75 °C h–1.
Check: Physics and units are reasonable
Exposition: Note that the horizontal temperature gradient is positive (T increases as y increases) and V is positive (south wind), yet this causes negative temperature change (cooling). We call this cold-air advection, because colder air is blowing in.
Sample Application
Given Figure 3.6b, except assume that higher in the figure corresponds to higher in the atmosphere (i.e., replace y with z). Suppose that the 5°C air is at a relative altitude that is 500 m higher than that of the 10°C air. If the updraft is 500 m/(10 hours), what is the temperature at the thermometer after 10 hours?
Find the Answer
Given: ∆z = 500 m, Tinitial = 5°C, W = 500 m/(10 h), ∆T/∆z = (5–10°C)/(500 m) = –0.01°C/m
Find: Tfinal = ? °C after ∆t = 10 h.
Looking at Figure 3.6c, one might guess that the final air temperature should be 10°C. But Figure 3.6c does not apply to vertical advection, because there is the added process of adiabatic expansion of the rising air.
The air that is initially 10°C in Figure 3.6b will adiabatically cool 9.8°C/km of rise. Here, it rises only 0.5 km in the 10 h, so it cools 9.8°C/2 = 4.9°C. Its final temperature is 10°C – 4.9°C = 5.1°C.
Check: Physics & units reasonable.
Exposition: The equations give the same result. Using eq. (3.28, 3.21 & 3.17): ∆T/∆t = – W · (∆T/∆z + Γd).
Since we need to apply this over ∆t = 10 h, multiply both sides by ∆t: ∆T = – W ·∆t · (∆T/∆z + Γd).
∆T = – (500m/10h) · (10h) · ( –0.01°C/m + 0.0098°C/m) = –500m · (–0.0002°C/m) = + 0.1°C.
This 0.1°C warming added to the initial temperature of 5°C gives the final temperature = 5.1°C.
Sample Application
The potential temperature of the air increases 5°C per 100 km distance east. If an east wind of 20 m s–1 is blowing, find the advective flux gradient, and the temperature change associated with this advection.
Find the Answer
Given: ∆θ/∆x = 5°C/100 km = 5x10–5 °C m–1 U = – 20 m s–1 (an east wind comes from the east)
Find: ∆F/∆y = ? °C s–1, and ∆T/∆t = ? °C s–1
Apply eq. (3.29): ∆F/∆x = (– 20 m s–1)·(5x10–5 °C m–1) = –0.001 °C s–1
Apply eq. (3.17) neglecting all other terms:
∆T/∆t = – ∆F/∆x = – (–0.001°C s–1) = +0.001 °C s–1
Check: Physics reasonable. Sign appropriate, because we expect warming as the warm air is blown toward us from the east in this example.
Exposition: ∆T/∆t = 3.6°C h–1, a rapid warming rate.
3.5.3. Molecular Conduction & Surface Fluxes
Molecular heat conduction is caused by microscopic-scale vibrations and movement of air molecules transferring some of their microscopic kinetic energy to adjacent molecules. Conduction is what gets heat from the solid soil surface or liquid ocean surface into the air. It also conducts surface heat further underground. Winds are not needed for conduction.
Vertical heat flux due to molecular conduction is:
\(\ \begin{align} \mathbb{F}_{z \text { cond }}=-k \cdot \frac{\Delta T}{\Delta z}\tag{3.32}\end{align}\)
where k is the molecular conductivity, which depends on the material doing the conducting. The molecular conductivity of air is k = 2.53x10–2 W·m–1·K–1 at sea-level under standard conditions.
The molecular conductivity for air is small, and vertical temperature gradients are also small in most of the atmosphere, so a good approximation is:
\(\ \begin{align} \frac{\Delta F_{x\ cond }}{\Delta x} \approx \frac{\Delta F_{y\ cond }}{\Delta y} \approx \frac{\Delta F_{z\ cond }}{\Delta z} \approx 0\tag{3.33}\end{align}\)
But near the ground, large vertical temperature gradients frequently occur in the bottom several mm of the atmosphere (Figure 3.7). If you have ever walked barefoot on a black asphalt parking lot or road on a hot summer day, you know that the surface temperatures can be burning hot to the touch (hotter than 50°C) even though the air temperatures at the height of your ankles can be 30°C or cooler. This large temperature gradient compensates for the small molecular conductivity of air, to create important vertical heat fluxes at the surface.
Sample Application
Suppose the temperature decreases from 50°C at the Earth’s surface to 30°C at 5 mm above ground, as in Figure 3.7. What is the vertical molecular heat flux?
Find the Answer
Given: ∆T = –20 °C, ∆z = 0.005 m k = 2.53x10–2 W·m–1·K–1
Find: Fz cond = ? W·m–2
Apply eq. (3.32) :
Fz cond = –( 2.53x10–2 W·m–1·K–1) · [–20°K/(0.005 m)] = 101.2 W·m–2
Check: Physics and units are reasonable.
Exposition: Although this is a fairly large heat flux into the bottom of the atmosphere, other processes described next (turbulence) can spread this heat over a layer of air roughly 1 km deep.

The bottom layer of the atmosphere that feels the influence of the earth’s surface (i.e., the bottom boundary of the atmosphere) is known as the atmospheric boundary layer (ABL). This 1 to 2 km thick layer is often turbulent, meaning it has irregular gusts and whorls of motion. Meteorologists have devised an effective turbulent heat flux that is the sum of molecular and turbulent heat fluxes (Figure 3.7), where turbulence is described in the next section. At the surface this effective flux is entirely due to molecular conduction, and above about 5 mm altitude the effective flux is mostly due to turbulence.
Instead of using eq. (3.32) to calculate molecular surface heat fluxes, most meteorologists approximate the effective surface turbulent heat flux, FH, using what are called bulk-transfer relationships. For windy conditions where most of the turbulence is caused by wind shear (change of wind speed or direction with altitude), you can use:
\(\ \begin{align} F_{H}=C_{H} \cdot M \cdot\left(\theta_{s f c}-\theta_{a i r}\right)\tag{3.34}\end{align}\)
or
\(\ \begin{align}F_{H} \cong C_{H} \cdot M \cdot\left(T_{s f c}-T_{a i r}\right)\tag{3.35}\end{align}\)
where (Tsfc, θsfc) are the temperature and potential temperature at the top few molecules (the skin) of the earth’s surface, (Tair , θair) are the corresponding values in the air at 2 m above ground, and the wind speed at altitude 10 m is M. The empirical coefficient CH is called the bulk heat-transfer coefficient. It is dimensionless, and varies from about 2x10–3 over smooth lakes or salt flats to about 2x10–2 for a rougher surface such as a forest. FH is a kinematic flux.
Sample Application
The wind is blowing at 10 m s–1 at height 10 m AGL. The 2 m air temperature is 15°C but the surface skin temperature is 30°C. What is the effective surface kinematic heat flux? Assume a surface of medium roughness having CH = 0.01 .
Find the Answer
Given: CH = 0.01 , M = 10 m s–1 at z = 10 m, Tsfc = 30°C , Tair = 15°C at z = 2 m
Find: FH = ? K·m·s–1
Apply eq. (3.35): FH = (1x10–2)·(10 m s–1)·(30–15°C) = 1.5 °C·m·s–1
Check: Physics and units are reasonable.
Exposition: Recall that the relationship between dynamic and kinematic heat flux is FH = ρ · Cp · FH. Thus, the dynamic heat flux is FH ≈ (1.2 kg m–3)·(1004 J kg–1 K–1)·(1.5 K·m·s–1) = 1807. W m–2. This is an exceptionally large surface heat flux — larger than the average solar irradiance of 1361 W·m–2. But such a heat flux could occur where cool air is advecting over a very hot surface.
For calm sunny conditions, turbulence is created by thermals of warm air rising due to their buoyancy. The resulting convective circulations cause so much stirring of the air that the ABL becomes a well mixed layer (ML). For this situation, you can use:
\(\ \begin{align} F_{H}=b_{H} \cdot w_{B} \cdot\left(\theta_{s f c}-\theta_{M L}\right)\tag{3.36}\end{align}\)
or
\(\ \begin{align}F_{H}=a_{H} \cdot w_{*} \cdot\left(\theta_{s f c}-\theta_{M L}\right)\tag{3.37}\end{align}\)
where aH = 0.0063, is a dimensionless empirical mixed-layer transport coefficient, and bH = 5x10–4 is called a convective transport coefficient. θML is the mid-mixed-layer potential temperature (at height 500 m for a ML that is 1 km thick).
The wB factor in eq. (3.36) is called the buoyancy velocity scale (m s–1):
\(\ \begin{align}w_{B}=\left[\frac{|g| \cdot z_{i}}{T_{v\ M L}} \cdot\left(\theta_{v\ s f c}-\theta_{v\ M L}\right)\right]^{1 / 2}\tag{3.38}\end{align}\)
for a ML of depth zi , and using gravitational acceleration |g| = 9.8 m s–2. (θv sfc , θv ML) are virtual potential temperatures of the surface skin and in the mid-mixed layer, and Tv is the absolute virtual temperature (Kelvins) in the mid mixed layer. Typical updraft speeds in thermals are of order 0.02·wB . To good approximation, the denominator in eq. (3.38) can be approximated by θv ML (also in units of K).
Another convective velocity scale w* is called the Deardorff velocity:
\(\ \begin{align}w_{*}=\left[\frac{|g| \cdot z_{i}}{T_{v}} \cdot F_{H s f c}\right]^{1 / 3}\tag{3.39}\end{align}\)
for a surface kinematic heat flux of FHsfc = FH. Often the Deardorff velocity is of order 1 to 2 m·s–1, and the relationship between the two velocity scales is w* ≈ 0.08·wB.
Later in the chapter, in the section on the Bowen ratio, you will see other formulas you can use to estimate FH. Bulk transfer relationships can be used for other scalar fluxes at the surface including the moisture flux. For this case, replace temperature or potential-temperature differences with humidity differences between the surface skin and the mixed layer.
Sample Application
What is the value of FH on a sunny day with no winds? Assume zi = 3 km, no clouds, dry air, θML = 290 K, and θsfc = 320 K.
Find the Answer
Given: θsfc = 320 K, θML = 290 K, zi = 3 km,
Find: Fz eff.sfc. = ? K·m·s–1
If the air is dry, then: θv = θ (from eq. 3.13). Apply eqs. (3.38) and (3.36):
\(w_{B}=\left[\frac{\left|9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right| \cdot 3000 \mathrm{m}}{290 \mathrm{K}} \cdot(320 \mathrm{K}-290 \mathrm{K})\right]^{1 / 2}
=\left(3041 \mathrm{m}^{2} \cdot \mathrm{s}^{-2}\right)^{12}=55.1 \mathrm{m} \cdot \mathrm{s}^{-1}\)
FH = (5x10–4)·(55.1 m·s–1)·(320 K – 290 K) = 0.83 K·m·s–1
Check: Physics & units are reasonable.
Exposition: Notice how the temperature difference between the surface and the air enters both in the eq. for wB and again for FH. Thus, greater differences drive greater surface heat flux.
Sample Application
Given an effective surface kinematic heat flux of 0.67 K·m·s–1 , find the Deardorff velocity for a dry, 1 km thick boundary layer of temperature 25°C
Find the Answer
Given: FH = 0.67 K·m·s–1 , zi = 1 km = 1000 m , Tv = T (because dry) = 25°C = 298 K.
Find: w* = ? m s–1
Apply eq. (3.39):
w* = [ (9.8 m·s–2)·(1000m)·(0.67 K·m·s–1)/(298K)]1 3 = 2.8 m s–1
Check: Physics & units are reasonable.
Exposition: Over land on hot sunny days, warm buoyant thermals often rise with a speed of the same order of magnitude as the Deardorff velocity.
3.5.4. Atmospheric Turbulence
Superimposed on the average wind are somewhat-random faster and slower gusts. This turbulence is caused by eddies in the air that are constantly being created, changing, and dying. They exist as a superposition of many different size swirls (3 mm to 3 km). One eddy might move a cold blob of air out of any fixed Eulerian region, but another eddy might move air that is warmer into that same region. Although we don’t try to forecast the heat transported by each individual eddy (an overwhelming task), we instead try to estimate the net heat flux caused by all the eddies. Namely, we resort to a statistical description of the effects of turbulence.
Turbulence in the air is analogous to turbulence in your teacup when you stir it. Namely, turbulence tends to blend all the ingredients into a uniform homogeneous mixture. In the atmosphere, the mixing homogenizes individual variables such as potential temperature, humidity, and momentum (wind). The mixing rate depends on the strength of the turbulence, which can vary in space and time. We will focus on mixing of heat (potential temperature) here.
3.5.4.1. Fair Weather (no thunderstorms)
In a turbulent atmospheric boundary layer (ABL), daytime turbulence caused by convective thermals can transport heat from the sun-warmed Earth’s surface and can distribute it more-or-less evenly through the ABL depth. The resulting turbulent heat fluxes decrease linearly with height as shown by the thick green line in Figure 3.7d. This line has a value at the bottom of the ABL as given by the effective surface flux (Fz bottom = FH), and at the top has a value of (Fz top ≈ –0.2·FH) on less windy days. Thus, the flux-divergence term for turbulence (during sunny fair weather, within domain 0 < z < zi ) is:
\(\ \begin{align}\frac{\Delta F_{z\ turb}}{\Delta z} \approx \frac{F_{z\ top}-F_{z\ bottom}}{z_{i}}\tag{3.40}\end{align}\)
\(\ \begin{align}\frac{\Delta F_{z\ turb}}{\Delta z} \approx \frac{-1.2 \cdot F_{H}}{z_{i}}\tag{3.41}\end{align}\)
for an ABL depth zi of 0.2 to 3 km.
When no storm clouds are present, the air at z > zi is often not turbulent during daytime:
\(\ \begin{align}\frac{\Delta F_{z\ turb}}{\Delta z} \approx 0 \quad above\ \mathrm{ABL}\ \text{top; for fair weather}\tag{3.42}\end{align}\)
During clear nights of fair weather, turbulence can be very small over most of the lower 3 km of troposphere, except in the very lowest 100 m where wind shears can still create occasional turbulence.
Sample Application
Given the Sample Application at the top of the previous page, what is the value for vertical flux divergence for this calm, sunny ABL?
Find the Answer
Given: FH = 0.83 K·m·s–1, zi = 3000 m
Find: ∆Fz turb/∆z = ? (K s–1)
Apply eq. (3.41):
\(\begin{aligned} \frac{\Delta F_{z} \operatorname{turb}}{\Delta z} & \approx \frac{-1.2 \cdot F_{H}}{z_{i}} \\ \frac{\Delta F_{z} \operatorname{turb}}{\Delta z} & \approx \frac{-1.2 \cdot(0.83 \mathrm{K} \cdot \mathrm{m} / \mathrm{s})}{3000 \mathrm{m}} \\ &=-0.000332 \mathrm{K} \cdot \mathrm{s}^{-1} \end{aligned}\)
Check: Physics and units are reasonable.
Exposition: Recall from eq. (3.17) that a negative vertical gradient gives a positive warming with time — appropriate for a sunny day. The amount of warming is about 1.2°C/h. You might experience this warming rate over 10 hours on a hot sunny day.
3.5.4.2. Stormy Weather
Sometimes horizontal advection can move warm air under colder air. This makes the atmosphere statically unstable, allowing thunderstorms to form. These storms try to undo the instability by overturning the air — allowing the warm air to rise and cold air to sink. But the result is so violently turbulent that much mixing also takes place. The end result can sometimes be an atmosphere with a vertical gradient close to that of the standard atmosphere, as was discussed in Chapter 1. Namely, the atmosphere experiences moist convective adjustment, to adjust the initial less-stable lapse rate to one that is more stable.
The standard atmospheric lapse rate (Γsa = –∆T/∆z ) is 6.5 K km–1. Suppose that the initial lapse rate before the thunderstorm forms is Γps (= –∆T/∆z). The amount of heat flux that is required to move the warm air up and cold air down during a storm lifetime of ∆t (≈1 h) is:
\(\ \begin{align}\frac{\Delta F_{z\ turb}}{\Delta z} \approx \frac{z_{T}}{\Delta t} \cdot\left[\Gamma_{p s}-\Gamma_{s a}\right] \cdot\left(\frac{1}{2}-\frac{z}{z_{T}}\right)\tag{3.43}\end{align}\)
where the troposphere depth is zT (≈11 km). An initially unstable environment gives a positive value for the factor enclosed by square brackets.
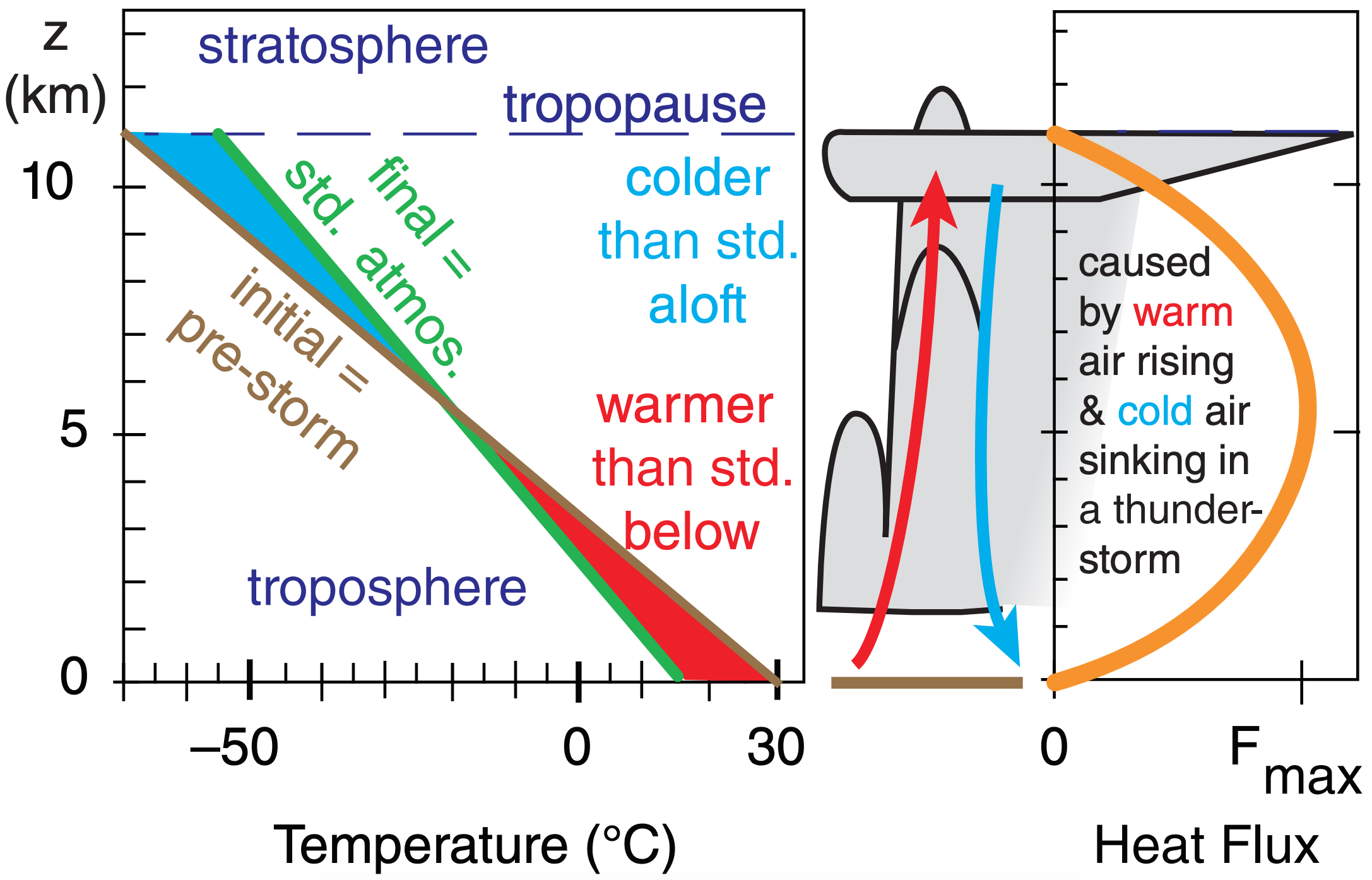
Because thunderstorm motions do not penetrate below ground, and assuming no flux above the top of the storm, then the vertical turbulent heat flux must be zero at both the top and bottom of the troposphere, as was sketched in Figure 3.8. The parabolic shape of the heat-flux curve has a maximum value of:
\(\ \begin{align}F_{\max }=z_{T}^{2} \cdot\left[\Gamma_{p s}-\Gamma_{s a}\right] /(8 \cdot \Delta t)\tag{3.44}\end{align}\)
The thunderstorm also affects the heat budget via warming at all thunderstorm altitudes where condensation exceeds evaporation. Cooling at the thunderstorm top can be caused by IR radiation from the anvil cloud up into space. These heating and cooling effects should be added to the heat redistribution (heat moved from the bottom to the top of the storm) caused by turbulence.
So far, we focused on vertical flux gradients and the associated heating or cooling. Turbulence can also mix air horizontally, but the net horizontal heat transport is often negligibly small for both fair and stormy weather, because background temperature changes so gradually with distance in the horizontal. Thus, at all locations, a reasonable approximation is:
\(\ \begin{align} \frac{\Delta F_{x\ turb}}{\Delta x} \approx \frac{\Delta F_{y\ turb}}{\Delta y} \approx 0\tag{3.45}\end{align}\)
Also, at locations with no turbulence there cannot be turbulent heat transport.
Sample Application
Suppose a pre-storm environment has a lapse rate of 9 °C km–1. a) What is the maximum value of vertical heat flux near the middle of the troposphere during a storm lifetime? b) Calculate the vertical flux gradient at 1 km altitude due to the storm.
Find the Answer
Given: Γps = 9 K km–1,
Find: (a) Fmax = ? K·m s–1 (b) ∆Fz turb/∆z = ? (K s–1)
Assume: Γsa = 6.5 K km–1, lifetime = ∆t = 1 h = 3600 s, zT = 11 km,
(a) Apply eq. (3.44):
Fmax =(11,000m)·(11km)·[(9–6.5)(K km–1)]/[8·(3600s)] = 10.5 K m s–1
(b) Apply eq. (3.43):
\(\frac{\Delta F_{z\ turb}}{\Delta z} \approx \frac{z_{T}}{\Delta t} \cdot\left[\Gamma_{p s}-\Gamma_{s a}\right] \cdot\left(\frac{1}{2}-\frac{z}{z_{T}}\right)\)
\(\frac{\Delta F_{z\ turb}}{\Delta z} \approx \frac{11 \mathrm{km}}{3600 \mathrm{s}} \cdot\left[(9-6.5) \frac{\mathrm{K}}{\mathrm{km}}\right] \cdot\left(\frac{1}{2}-\frac{1 \mathrm{km}}{11 \mathrm{km}}\right)\)
\(\Delta F_{z\ turb} / \Delta z=0.0031 \mathrm{K} \mathrm{s}^{-1}\)
Check: Physics and units are reasonable.
Exposition: The magnitude of the max heat flux due to thunderstorms is much greater than the heat flux due to thermals in fair weather. Thunderstorms move large amounts of heat upward in the troposphere.
Based on Figure 3.8, we would anticipate that storm turbulence should cool the bottom half of the stormy atmosphere. Indeed, the minus sign in eq. (3.17) combined with the positive sign of answer (b) above gives the expected cooling, not heating.
3.5.5. Solar and IR Radiation
We will split this topic into short-wave (solar) and long-wave (IR) radiation. Clear air is mostly transparent to solar radiation. Thus, the amount of shortwave radiation entering an air volume nearly equals the amount leaving. No flux gradient means that, to good approximation, you can neglect the direct solar heating of the air. However, sunlight is absorbed at the Earth’s surface, which causes surface heat fluxes as already discussed. Sunlight is also absorbed in clouds or smoke, which can cause warming.
IR radiation is more complex, because air strongly absorbs a large portion of IR radiation flowing into a fixed volume, and re-radiates IR radiation outward in all directions. Radiation emission is related to T4, according to the Stefan-Boltzmann law. In horizontal directions having weak temperature gradients, radiative flux divergence is negligibly small:
\(\ \begin{align}\frac{\Delta F_{x\ rad}}{\Delta x} \approx \frac{\Delta F_{y\ rad}}{\Delta y} \approx 0\tag{3.46}\end{align}\)
But in the vertical, recall that temperature decreases with increasing altitude. Hence, more radiation would be lost upward from warmer air in the lower troposphere than is returned downward from the colder air aloft, which causes net cooling.
\(\ \begin{align}\frac{\Delta F_{z\ r a d}}{\Delta z} \approx 0.1 \ to \ 0.2\ (\mathrm{K} / \mathrm{h})\tag{3.47}\end{align}\)
Expert scientists and engineers often solve problems, organize knowledge, and perceive structure differently than students and other novices.
| Problem Solving | Novice | Expert |
| ... is ... | a recall task | a process |
| ... begins with ... | hunt for “the equation” | qualitative analysis |
| ... uses classification based on ... | surface features | deep structure |
| ...tools include ... | “the equation” | graphs, limits, diagrams, conservation laws, units, ... |
| Organizing Knowledge | Novice | Expert |
| Memory recall is ... | piecemeal | effortless retrieval of relevant collected facts |
| Reasoning by ... | jumping to hasty, unfounded conclusions | fast mental scan through a chain of possibilities |
| Conflicting data, ideas & conclusions are... | not recognized | recognized, pointing to need for more info |
| Related ideas are... | memorized as separate facts | integrated into a coherent big picture |
| Structure Perception | Novice | Expert |
| Cues about the structure are ... | missed | recognized and trigger new lines of thought |
| Disparate instances are... | separately classified based on surface features | recognized as having the same underlying structure |
| Tasks are performed... | before thinking about the organization | after data is organized to find structure |
| Theories that don’t agree with data ... | are used without revision | identify ideas ripe for revision |
(Paraphrased from Wendy Adams, Carl Wieman, Dan Schwartz, & Kathleen Harper.)
3.5.6. Internal Sources such as Latent Heat
Suppose ∆mcondensing kilograms of water vapor inside the storm condenses into liquid droplets and does not re-evaporate. It would release Lv·∆mcondensing Joules of latent heat. If this heating is spread vertically through the whole thunderstorm (a gross simplification) of air mass mair, then the heating is:
\(\ \begin{align} \frac{\Delta S o}{C_{p} \cdot \Delta t}=\frac{L_{v}}{C_{p}} \cdot \frac{\Delta m_{\text {condensing}}}{m_{\text {air}} \cdot \Delta t}\tag{3.48}\end{align}\)
Because this warming does not require a heat flux across the storm boundaries, we define it as a “source term” that is internal to the thunderstorm. An opposite case of existing suspended cloud droplets that evaporate would yield the same equation, but with opposite sign as indicates net cooling.
In a real thunderstorm, some of the water vapor that initially condensed into cloud droplets can later evaporate. But any precipitation reaching the ground represents condensation that did not reevaporate. Hence, we can use rainfall rate (RR) to estimate the internal latent heating rate:
\(\ \begin{align}\frac{\Delta S o}{C_{p} \cdot \Delta t}=\frac{L_{v}}{C_{p}} \cdot \frac{\rho_{l i q}}{\rho_{a i r}} \cdot \frac{R R}{z_{T r o p}}\tag{3.49}\end{align}\)
where the storm is assumed to fill a column of tropospheric air of depth zTrop, liquid-water density is ρliq = 1000 kg·m–3, latent-heat to specific heat ratio is Lv/Cp = 2500 K·kgair·kgliq–1, and column-averaged air density is ρair = 0.689 kg·m–3 for zTrop = 11 km.
Combining some of the values in eq. (3.49) gives:
\(\ \begin{align}\frac{\Delta S o}{C_{p} \cdot \Delta t}=a \cdot R R\tag{3.50}\end{align}\)
where a = 0.33 K (mm of rain)–1, and RR has units [(mm of rain) s–1]. Divide by 3600 for RR in mm h–1.
3.5.7. Simplified Eulerian Net Heat Budget
You can insert the flux-gradient approximations from the previous subsections into eqs. (3.17 or 3.18) for the first law of thermo. Although the result looks complicated, you can simplify it by assuming the following are negligible within a fixed air volume: (1) vertical temperature advection by the mean wind; (2) horizontal turbulent heat transport; (3) molecular conduction; (4) short-wave heating of the air; (5) constant IR cooling.
You then get the following approximate Eulerian net heat-budget equation:
\(\ \begin{align}\frac{\Delta T}{\Delta t}|_{x, y, z} &=-\left[U \cdot \frac{\Delta T}{\Delta x}+V \cdot \frac{\Delta T}{\Delta y}\right]-0.1 \frac{\mathrm{K}}{\mathrm{h}}-\frac{\Delta F_{z\ turb}(\theta)}{\Delta z}+\frac{L_{v}}{C_{p}} \cdot \frac{\Delta m_{\text {condensing}}}{m_{\text {air}} \cdot \Delta t}\tag{3.51}\end{align}\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ advection \ \ \ \ \ radiation \ \ \ \ turbulence \ \ \ \ \ \ latent heat\)
Later in this book you will see similar budget equations for other variables such as water vapor or momentum. In the turbulence term above, the (θ) indicates that this term is for heat flux divergence. Any of the terms on the right-hand side can be zero if the process it represents (advection, radiation, turbulence, condensation) is not active.
The net heat budget is important because you can use it to forecast air temperature at any altitude. Or, if you already know how the air temperature changes with time, you can use the net heat budget to see which processes are most important in causing this change.
The net heat budget applies to a volume of air having a finite mass. For the special case of the Earth’s surface (infinitesimally thin; having no mass), you can write a simplified heat budget, as described next.
Sample Application
Suppose a thunderstorm rains at rate 4 mm h–1. What is the average heating rate in the troposphere?
Find the Answer
Given: RR = 4 mm·h–1.
Find: ∆So/(Cp·∆t) = ? K·h–1
Apply eq. (3.50): ∆So/(Cp·∆t) = 0.33 (K mm–1)· (4 mm h–1) = 1.32 K·h–1
Check: Physics and units are reasonable.
Exposition: For fixed Eulerian volumes losing liquid water as precipitation, this heating rate is significant.
Sample Application
For a fixed Eulerian volume, what temperature increase occurs in 2 h if ∆mcond/mair = 1 gwater kgair–1, FH sfc = 0.25 K·m·s–1 into a 1 km thick boundary layer, U = 0, V = 10 m s–1, and ∆T/∆y = –2°C/100 km. Hint, approximate Lv/Cp ≈ 2.5 K (gwater kgair–1)–1.
Find the Answer
Given: (see above)
Find: ∆T = ? °C over a 2 hour period
For each term in eq. (3.51), multiply by ∆t:
\(\begin{aligned} \text { Lat.Heat_Source } \cdot \Delta t=\left(2.5 \frac{\mathrm{K} \cdot \mathrm{kg}_{\text {air }}}{\mathrm{g}_{\text {water }}}\right) \cdot\left(1 \frac{\mathrm{g}_{\text {water }}}{\mathrm{kg}_{\text {air }}}\right) = + 2.5^{\circ} \mathrm{C} \end{aligned}\)
Turb \(\cdot \Delta t=-\frac{-1.2 \cdot(0.25 \mathrm{K} \cdot \mathrm{m} / \mathrm{s})}{1000 \mathrm{m}} \cdot(7200 \mathrm{s})=+ 2.16^{\circ} \mathrm{C}\)
Adv \(\cdot \Delta t=-\left[(10 \mathrm{m} / \mathrm{s}) \cdot\left(\frac{-2^{\circ} \mathrm{C}}{100000 \mathrm{m}}\right)\right] \cdot(7200 \mathrm{s})=+ 1.44^{\circ} \mathrm{C}\)
Rad \(\cdot \Delta t=\left(-0.1 \frac{\mathrm{K}}{\mathrm{h}}\right) \cdot(2 \mathrm{h}) \quad=-0.2^{\circ} \mathrm{C}\)
Combining all the terms gives:
∆T = (Latent + Turb + Adv + Rad) = (2.5 + 2.16 + 1.44 – 0.2)°C = 5.9 °C over 2 hours.
Check: Physics and units are reasonable.
Exposition: For this contrived example, all the terms (except advection in the x direction) were important. Many of these terms can be estimated by looking at weather maps. For example, cloudy conditions might shade the sun during daytime and reduce the surface heat flux. These same clouds can trap IR radiation, causing the net radiative loss to be near zero below cloud base. But if there are no clouds (i.e., no condensation) and no falling precipitation that evaporates on the way down, then the latent-heating term would be zero.
So there is no fixed answer for the Eulerian heat budget — it varies as the weather varies.


