18.5: Wind
- Page ID
- 9648
For any given weather condition, there is a theoretical equilibrium wind speed, called the geostrophic wind G, that can be calculated for frictionless conditions (see the Atmos. Forces & Winds chapter). However, steady-state winds in the ABL are usually slower than geostrophic (i.e., subgeostrophic) because of frictional and turbulent drag of the air against the surface, as was illustrated in Fig. 18.9a.
Turbulence continuously mixes slower air from close to the ground with faster air from the rest of the ABL, causing the whole ABL to experience drag against the surface and to be subgeostrophic. This vertically averaged steady-state ABL wind MBL is derived in the Atmos. Forces & Winds chapter. The actual wind speed over a large central region of the ABL is nearly equal to the theoretical MBL speed.
Winds closer to the surface (in the surface layer, SL) are even slower (Fig. 18.9a). Wind-profile shapes in the SL are empirically found to be similar to each other when scaled with appropriate length and velocity scales. This approach, called similarity theory, is described later in this section.
18.5.1. Wind Profile Evolution
Over land during fair weather, the winds often experience a diurnal cycle as illustrated in Fig. 18.18. For example, a few hours after sunrise, say at 9 AM local time, there is often a shallow mixed layer, which is 300 m thick in this example. Within this shallow mixed layer the ABL winds are uniform with height, except near the surface where winds approach zero.
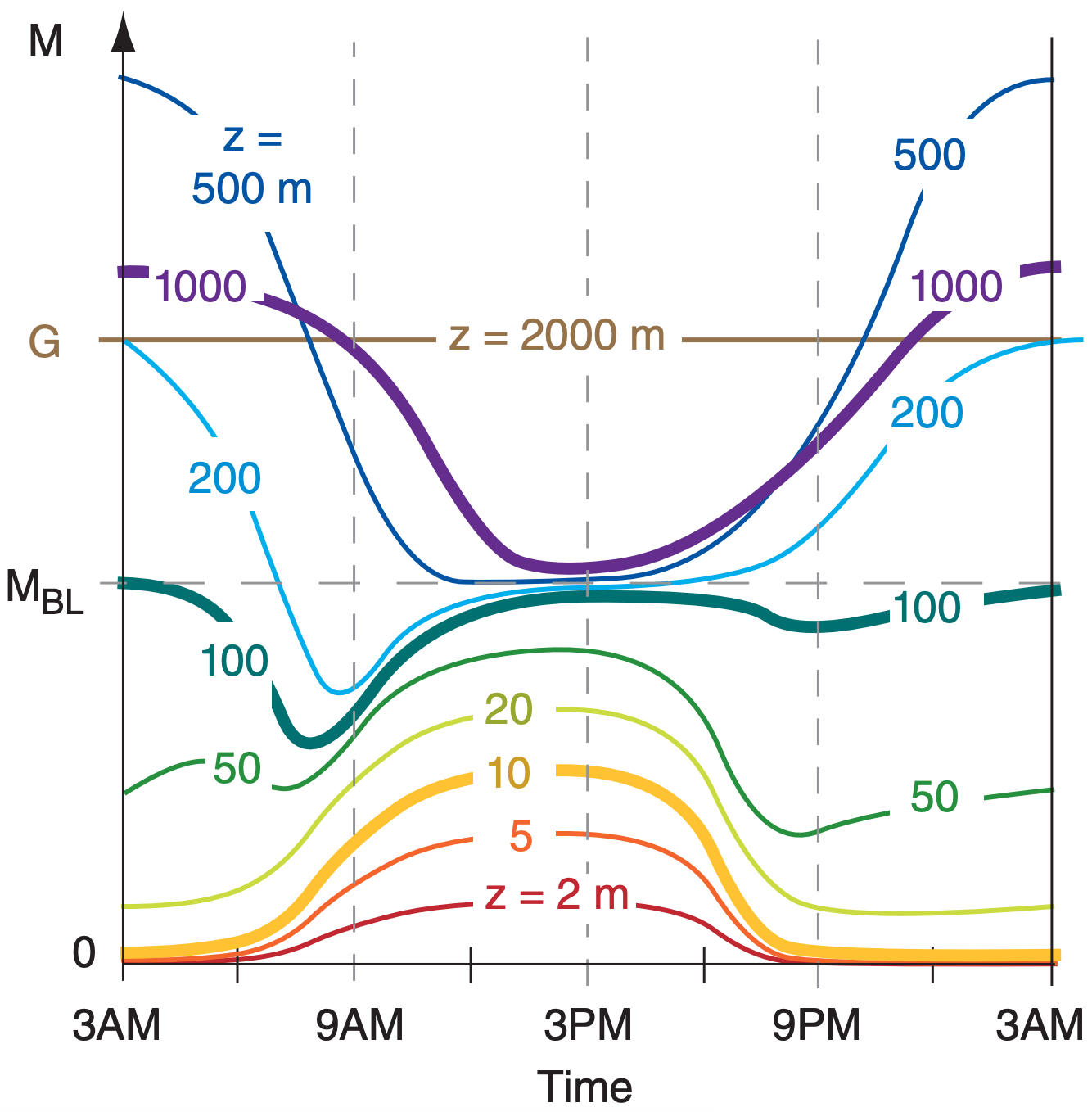
As the day progresses, the mixed layer deepens, so by 3 PM a deep layer of subgeostrophic winds fills the ABL. Winds remain moderate near the ground as turbulence mixes down faster winds from higher in the ABL. After sunset, turbulence intensity usually diminishes, allowing surface drag to reduce the winds at ground level. However, without turbulence, the air in the mid-ABL no longer feels drag against the surface, and begins to accelerate.
By 3 AM, the winds a few hundred meters above ground can be supergeostrophic, even though the winds at the surface might be calm. This low-altitude region of supergeostrophic winds is called a nocturnal jet. This jet can cause rapid horizontal transport of pollutants, and can feed moisture into thunderstorms. Then, after sunrise, the nocturnal jet disappears as turbulence causes surface drag to increase and as slower air is mixed from below.
For measurements made at fixed heights on a very tall tower, the same wind-speed evolution is shown in Fig. 18.19. Below 20 m altitude, winds are often calmer at night, and increase in speed during daytime. The converse is true above 1000 m altitude, where winds are reduced during the day because of turbulent mixing with slower near-surface air, but become faster at night when turbulence decays.
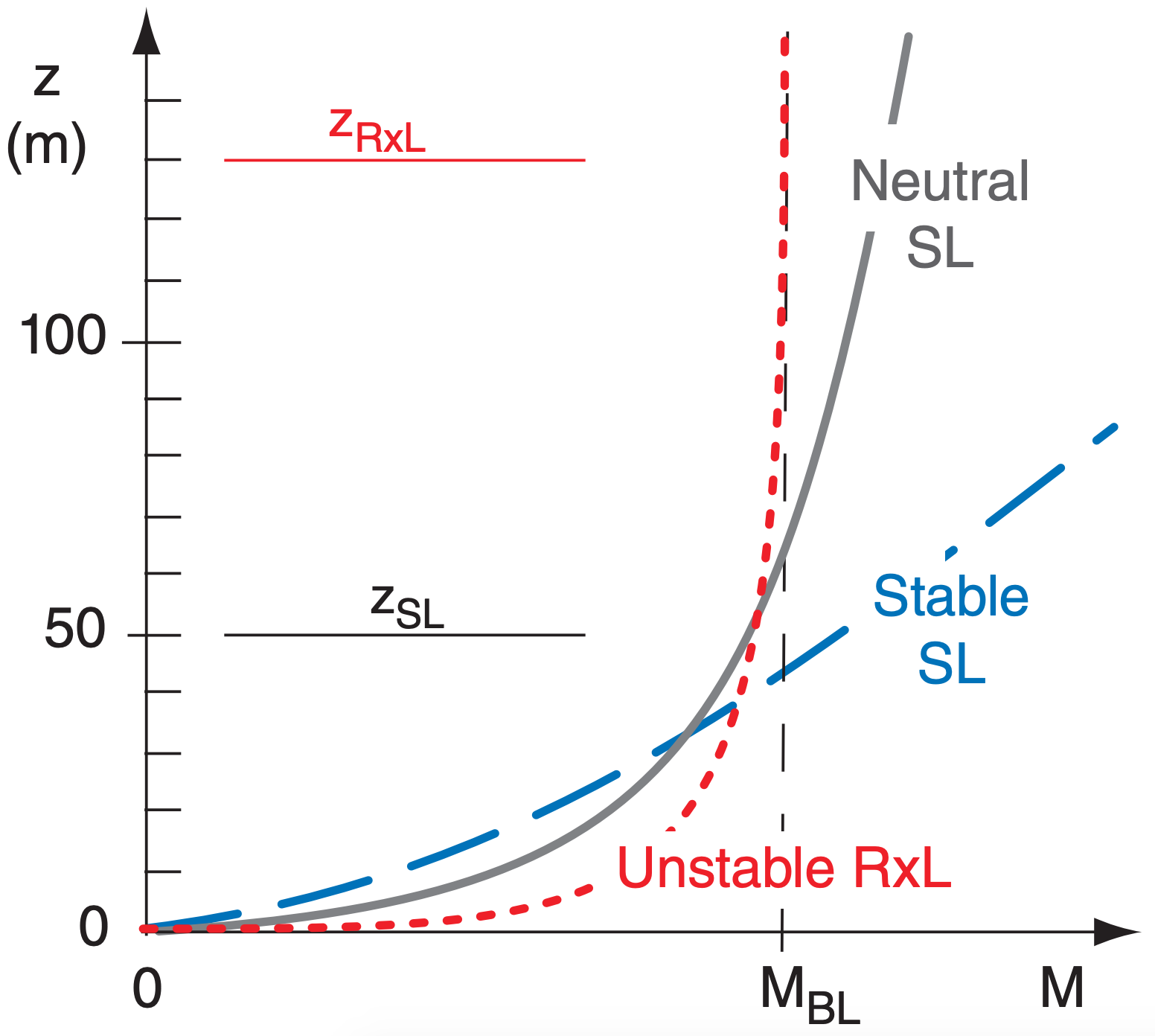
At the ABL bottom, near-surface wind speed profiles have been found empirically (via observations). In the bottom 5% of the statically neutral ABL is the surface layer, where wind speeds increase roughly logarithmically with height (Fig. 18.20).
For the statically stable surface layer, this logarithmic profile changes to a more linear form (Fig. 18.20). Winds close to the ground become slower than logarithmic, or near calm. Winds just above the surface layer are often not in steady state, and can temporarily increase to faster than geostrophic (supergeostrophic) in a process called an inertial oscillation (Figs. 18.9b and 18.20).
The bottom 20% of the convective (unstable) ABL is called the radix layer (RxL). Winds in the RxL have an exponential power-law relationship with height. The RxL has faster winds near the surface, but slower winds aloft than the neutral logarithmic profile. After a discussion of drag at the ground, these three wind cases at the bottom of the ABL will be described in more detail.
18.5.2. Drag, Stress, Friction Velocity & Roughness Length
The frictional force between two objects such as the air and the ground is called drag. One way to quantify drag is by measuring the force required to push the object along another surface. For example, if you place your textbook on a flat desk, after you first start it moving you must continue to push it with a certain force (i.e., equal and opposite to the drag force) to keep it moving. If you stop pushing, the book stops moving.
Your book contacts the desk with a certain surface area. Generally, larger contact area requires greater force to overcome friction. The amount of friction force per unit surface contact area is called stress, \(\ \tau\), and acts parallel to the surface. Contrast this with pressure, which is defined as a force per unit area that is perpendicular to the surface. Units of stress are N m–2 (see Appendix A), and could also be expressed as Pascals (Pa) or kiloPascals (kPa).
Stress is felt by both objects that are sliding against each other. For example, if you stack two books on top of each other, then there is friction between both books, as well as between the bottom book and the table. In order to push the bottom book in one direction without moving the top book relative to the table, you must apply a force to the top book in the opposite direction as the bottom book.
| Table 18-1. The Davenport-Wieringa roughness-length zo (m) classification, with approximate drag coefficients CD (dimensionless). | |||
| zo (m) | Classification | CD | Landscape |
|---|---|---|---|
| 0.0002 | sea | 0.0014 | sea, paved areas, snowcovered flat plain, tide flat, smooth desert |
| 0.005 | smooth | 0.0028 | beaches, pack ice, morass, snow-covered fields |
| 0.03 | open | 0.0047 | grass prairie or farm fields, tundra, airports, heather |
| 0.1 | roughly open | 0.0075 | cultivated area with low crops & occasional obstacles (single bushes) |
| 0.25 | rough | 0.012 | high crops, crops of varied height, scattered obstacles such as trees or hedgerows, vineyards |
| 0.5 | very rough | 0.018 | mixed farm fields and forest clumps, orchards, scattered buildings |
| 1.0 | closed | 0.030 | regular coverage with large-sized obstacles with open spaces roughly equal to obstacle heights, suburban houses, villages, mature forests |
| ≥ 2 | chaotic | ≥0.062 | centers of large towns and cities, irregular forests with scattered clearings |
Think of air within the ABL as a stack of layers of air, much like a stack of books. Each layer feels stress from the layers above and below it. The bottom layer feels stress against the ground, as well as from the layer of air above. In turn, the surface feels a stress due to air drag. Over the ocean, this wind stress drives the ocean currents.
In the atmosphere, stress caused by turbulent motions is many orders of magnitude greater than stress caused by molecular viscosity (see the INFO box on this page). For that reason, we often speak of turbulent stress instead of frictional stress, and turbulent drag rather than frictional drag. This turbulent stress is also called a Reynolds stress, after Osborne Reynolds who related this stress to turbulent gust velocities in the late 1800s.
Because air is a fluid, it is often easier to study the stress τ per unit density ρ of air. This is called the kinematic stress. The kinematic stress against the Earth’s surface is given the symbol u* 2, where u* is called the friction velocity:
\(\ \begin{align}u_{*}^{2}=|\tau / \rho|\tag{18.10}\end{align}\)
Typical values range from u* = 0 during calm winds to u* = 1 m s–1 during strong winds. Moderate-wind values are often near u* = 0.5 m s–1.
For fluid flow, turbulent stress is proportional to wind speed squared, and also increases with surface roughness. A dimensionless drag coefficient CD relates the kinematic stress to the wind speed M10 at z = 10 m.
\(\ \begin{align}u_{*}^{2}=C_{D} \cdot M_{10}^{2}\tag{18.11}\end{align}\)
The drag coefficient ranges from CD = 2x10–3 over smooth surfaces to 2x10–2 over rough or forested surfaces (Table 18-1). It is similar to the bulk heattransfer coefficient of the Heat chapter.
The surface roughness is usually quantified as an aerodynamic roughness length zo. Table 18- 1 shows typical values of the roughness length for various surfaces. Rougher surfaces such as sparse forests have greater values of roughness length than smoother surfaces such as a frozen lake. Roughness lengths in this table are not equal to the heights of the houses, trees, or other roughness elements.
For statically neutral air flow, there is a relationship between drag coefficient and aerodynamic roughness length:
\(\ \begin{align}C_{D}=\frac{k^{2}}{\ln ^{2}\left(z_{R} / z_{0}\right)}\tag{18.12}\end{align}\)
where k = 0.4 is the von Kármán constant, and zR = 10 m is a reference height defined as the standard anemometer height for measuring “surface winds”. For statically stable conditions, air becomes less turbulent and the drag coefficient decreases. For statically unstable conditions, use the relationships in section 10.3.5 to estimate turbulent drag.
Sample Application
Find the drag coefficient in statically neutral conditions to be used with standard surface winds of 5 m s–1, over (a) villages, and (b) grass prairie. Also, find the friction velocity and surface stress.
Find the Answer
Given: zR = 10 m for “standard” winds
Find: CD = ? (dimensionless), u* = ? m s–1, \(\ \tau\) = ? N m–2
Use Table 18-1:
(a) zo = 1 m for villages. (b) zo = 0.03 m for prairie
Use eq. (18.12) for drag coefficient:
\(\ \text { (a) } C_{D}=\frac{0.4^{2}}{\ln ^{2}(10 \mathrm{m} / 1 \mathrm{m})}=\underline{\bf{0.030}}(\text { dimensionless })\)
\(\ \text { (b) } C_{D}=\frac{0.4^{2}}{\ln ^{2}(10 \mathrm{m} / 0.03 \mathrm{m})}=\underline{\bf{0.0047}}(\text { dimensionless })\)
Use eq. (18.11) for friction velocity:
(a) u*2 = CD·M102 = 0.03·(5m s–1)2 = 0.75 m2·s–2
Thus u* = 0.87 ms–1.
(b) Similarly, u* = 0.34 ms–1.
Use eq. (18.10) for surface stress, and assume ρ = 1.2 kg m–3:
\(\
\text { (a) } \tau=\rho \cdot u_{*}^{2}=\left(1.2 \mathrm{kg} \mathrm{m}^{-3}\right) \cdot\left(0.75 \mathrm{m}^{2} \mathrm{s}^{-2}\right)=\\
\left.\tau=0.9 \mathrm{kg} \cdot \mathrm{m}^{-1} \cdot \mathrm{s}^{-2}=\underline{\bf{0.9}} \mathrm{Pa} \text { (using Appendix } \mathrm{A}\right)
\)
\(\ \text { (b) } \tau=0.14 \mathrm{kg} \cdot \mathrm{m}^{-1} \cdot \mathrm{s}^{-2}=\underline{\bf{0.14}} \mathrm{Pa}\)
Check: Units OK. Physics OK.
Exposition: The drag coefficient, friction velocity, and stress are smaller over smoother surfaces.
In this development we examined the stress for fixed wind speed and roughness. However, in nature, greater roughness & greater surface drag causes slower winds (see the Atmos. Forces & Winds chapter).
Suppose that u* = 0.5 m s–1 during statically neutral conditions at sea level. Eq. (18.10) give the turbulent (Reynolds) stress: \(\ \tau_{t u r b}=\rho \cdot u_{*}^{2}\)
= (1.225 kg m–3)·(0.5 m s–1)2 = 3.06x10–1 Pa.
The wind shear associated with this stress is given by the derivative of eq. (18.14a): ∆M/∆z = u* /(k·z), where k = 0.4 is the von Kármán constant. At z = 10 m, the shear is ∆M/∆z = (0.5 m·s–1)/(0.4·10m) = 0.125 s–1.
Molecular stress is \(\ \tau_{m o l.}\) = µ·∆M/∆z, where the molecular viscosity of air is roughly µ = 1.789x10–5 kg m–1 s–1. Using this with the shear of the previous paragraph gives \(\ \tau_{m o l.}\) = 2.24x10–6 Pa. Thus, molecular stress can be neglected compared to turbulent stress.
Combining the previous two equations gives an expression for friction velocity in terms of surface wind speed and roughness length for statically neutral conditions:
\(\ \begin{align} u_{*}=\frac{k \cdot M_{10}}{\ln \left[z_{R} / z_{0}\right]}\tag{18.13}\end{align}\)
The physical interpretation is that faster winds over rougher surfaces causes greater kinematic stress.
Sample Application
If the wind speed is 20 m s–1 at 10 m height over an orchard, find the friction velocity.
Find the Answer
Given: M10 = 20 m s–1 at zR = 10 m, zo = 0.5 m
Find: u* = ? m s–1
Use eq. (18.13):
u* = (0.4)·(20 m s–1)/ln(10m/0.5m) = 2.67 ms–1
Check: Units OK. Magnitude OK.
Exposition: This corresponds to a large stress on the trees, which could make the branches violently move, causing some fruit to fall.
18.5.3. Log Profile in the Neutral Surface Layer
Wind speed M is zero at the ground (more precisely, at a height equal to the aerodynamic roughness length). Speed increases roughly logarithmically with height in the statically neutral surface layer (bottom 50 to 100 m of the ABL), but the shape of this profile depends on the surface roughness:
\(\ \begin{align}M(z)=\frac{u_{*}}{k} \ln \left(\frac{z}{z_{o}}\right) \quad \text { for } z \geq z_{0}\tag{18.14a}\end{align}\)
Alternately, if you know wind speed M1 at height z1, then you can calculate wind speed M2 at any other height z2:
\(\ \begin{align}M_{2}=M_{1} \cdot \frac{\ln \left(z_{2} / z_{o}\right)}{\ln \left(z_{1} / z_{o}\right)}\tag{18.14b}\end{align}\)
Many weather stations measure the wind speed at the standard height z1 = 10 m.
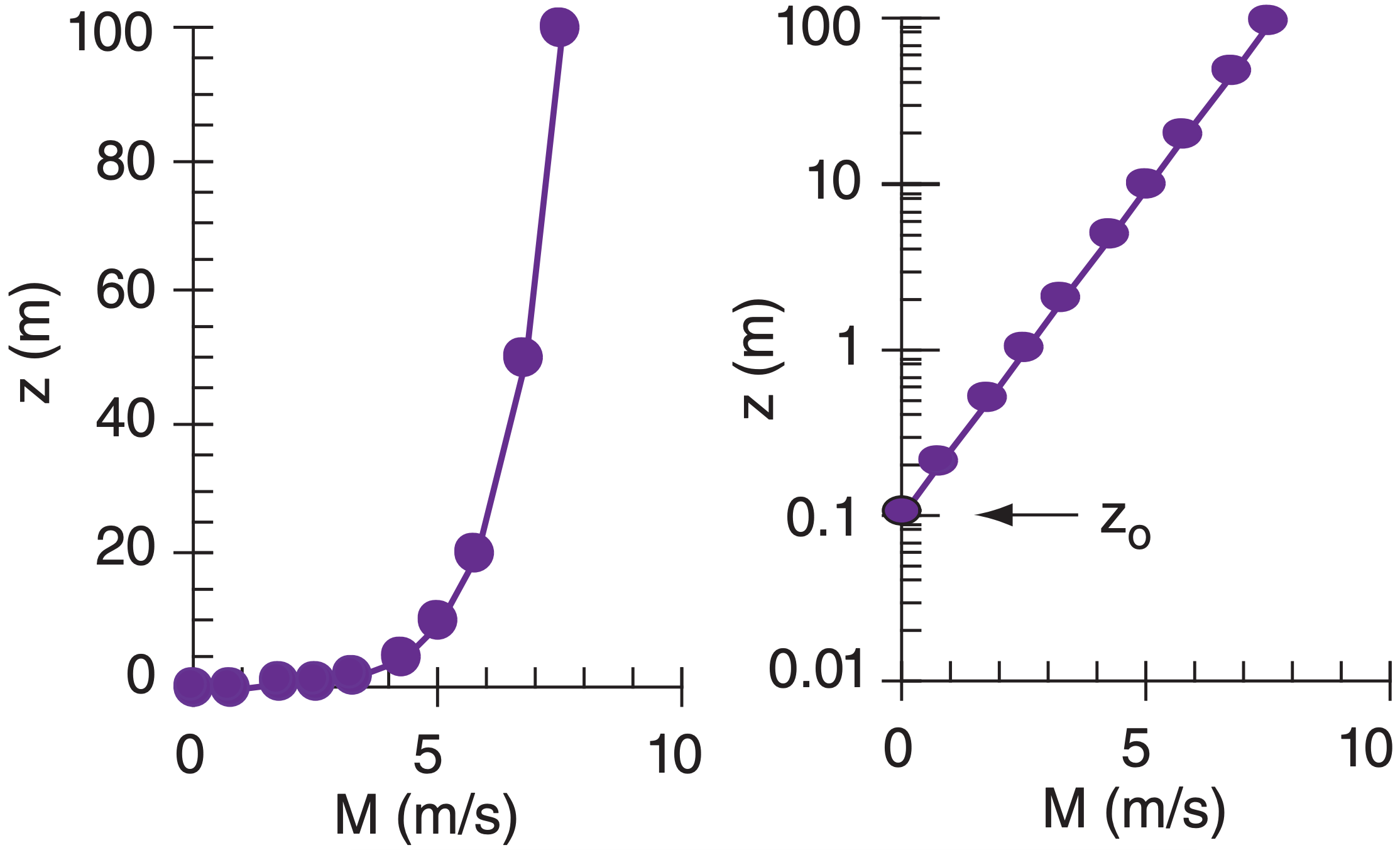
An example of the log wind profile is plotted in Fig. 18.21. A perfectly logarithmic wind profile (i.e., eq. 18.14) would be expected only for neutral static stability (e.g., overcast and windy) over a uniform surface. For other static stabilities, the wind profile varies slightly from logarithmic.
On a semi-log graph, the log wind profile would appear as a straight line. You can determine the roughness length by measuring the wind speeds at two or more heights, and then extrapolating the straight line in a semi-log graph to zero wind speed. The z-axis intercept gives the roughness length.
Sample Application
On an overcast day, a wind speed of 5 m s–1 is measured with an anemometer located 10 m above ground within an orchard. What is the wind speed at the top of a 25 m smoke stack?
Find the Answer
Given: M1 = 5 m s–1 at z1 = 10 m Neutral stability (because overcast)
zo = 0.5 m from Table 18-1 for an orchard
Find: M2 = ? m s–1 at z2= 25 m
Sketch:

Use eq. (18.14b):
\(\ M_{2}=5(\mathrm{m} / \mathrm{s}) \cdot \frac{\ln (25 \mathrm{m} / 0.5 \mathrm{m})}{\ln (10 \mathrm{m} / 0.5 \mathrm{m})}=\underline{\mathbf{6 .53} \mathrm{m} \mathrm{s}}^{-1}\)
Check: Units OK. Physics OK. Sketch OK.
Exposition: Hopefully the anemometer is situated far enough from the smoke stack to measure the true undisturbed wind.
18.5.4. Log-Linear Profile in Stable Surface Layer
During statically stable conditions, such as at nighttime over land, wind speed is slower near the ground, but faster aloft than that given by the log wind profile. This is because turbulence is weaker, causing less mixing and less homogenization of winds. The profile in the stable surface layer is empirically described by a log-linear profile formula with both a logarithmic and a linear term in z:
\(\ \begin{align}M(z)=\frac{u_{*}}{k}\left[\ln \left(\frac{z}{z_{o}}\right)+6 \frac{z}{L}\right]\tag{18.15}\end{align}\)
where M is wind speed at height z, k = 0.4 is the von Kármán constant, zo is the aerodynamic roughness length, and u* is friction velocity. As height increases, the linear term dominates over the logarithmic term, as sketched in Fig. 18.20.
An Obukhov length L is defined as:
\(\ \begin{align}L=\frac{-u_{*}^{3}}{k \cdot\left(|g| / T_{v}\right) \cdot F_{H S f c}}\tag{18.16}\end{align}\)
where |g| = 9.8 m s–2 is gravitational acceleration magnitude, Tv is the absolute virtual temperature, and FHsfc is the kinematic surface heat flux. L has units of m, and is positive during statically stable conditions (because FHsfc is negative then). The Obukhov length can be interpreted as the height in the stable surface layer below which shear production of turbulence exceeds buoyant consumption.
Sample Application (§)
For a friction velocity of 0.3 m s–1, aerodynamic roughness length of 0.02 m, average virtual temperature of 300 K, and kinematic surface heat flux of –0.05 K·m s–1 at night, plot the wind-speed profile in the surface layer. (Compare profiles for statically stable and neutral conditions.)
Find the Answer
Given: u* = 0.3 m s–1, zo = 0.02 m, Tv = 300 K, FHsfc = –0.05 K·m s–1
Find: M(z) = ? m s–1
Use eq. (18.16):
L = –(0.3m s–1)3/[0.4·(9.8m·s–2)·(–0.05K·m s–1)/(300K)] = 41.3 m
Use eq. (18.14a) for M in a neutral surface layer.
For example, at z = 50 m:
M = [(0.3m s–1)/0.4] · ln(50m/0.02m) = 5.9 m s–1
Use eq. (18.15) for M in a stable surface layer.
For example, at z = 50 m: M = [(0.3m s–1)/0.4] · [ln(50m/0.02m) + 6·(50m/41.3m)] = 11.3 m s–1
Use a spreadsheet to find M at the other heights:
| z (m) | M(m s–1)neutral | M (m s–1)stable |
| 0.02 | 0.0 | 0.0 |
| 0.05 | 0.7 | 0.7 |
| 0.1 | 1.2 | 1.2 |
| 0.2 | 1.7 | 1.7 |
| 0.5 | 2.4 | 2.5 |
| 1 | 2.9 | 3.0 |
| 2 | 3.5 | 3.7 |
| 5 | 4.1 | 4.7 |
| 10 | 4.7 | 5.7 |
| 20 | 5.2 | 7.4 |
| 50 | 5.9 | 11.3 |
| 100 | 6.4 | 17.3 |
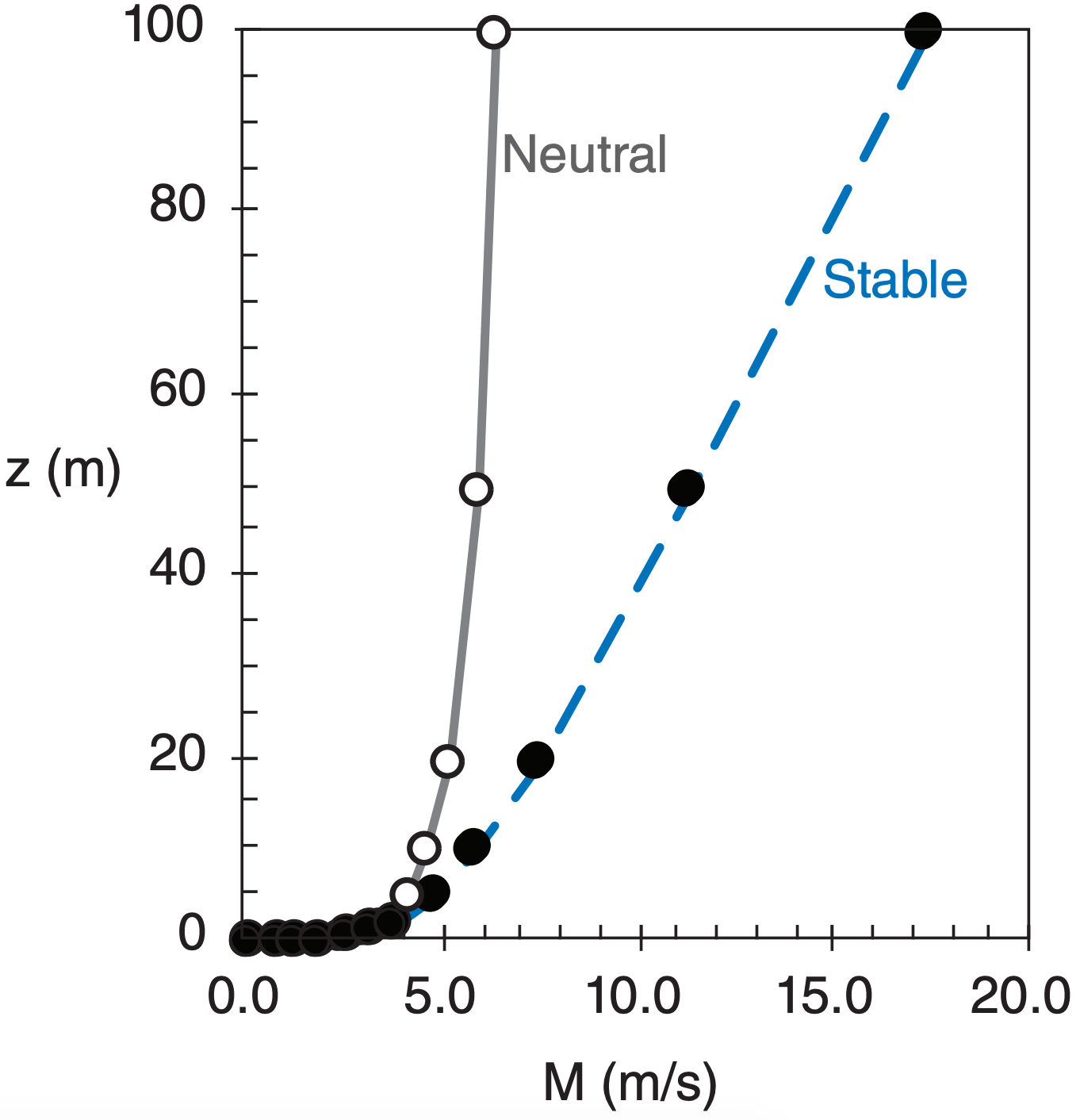
Check: Units OK. Physics OK. Plot OK.
Exposition: Open circles are for neutral, solid are for statically stable. The linear trend is obvious in the wind profile for the stable boundary layer.
18.5.5. Profile in the Convective Radix Layer
For statically unstable ABLs with vigorous convective thermals, such as occur on sunny days over land, wind speed becomes uniform with height a short distance above the ground. Between that uniform wind-speed layer and the ground is the radix layer (RxL). The wind speed profile in the radix layer is:
\(\ \begin{align}M(z)=M_{B L} \cdot\left(\zeta_{*}^{D}\right)^{A} \cdot \exp \left[A \cdot\left(1-\zeta_{*}^{D}\right)\right] \text { for } 0 \leq \zeta \leq 1.0\tag{18.17a}\end{align}\)
and
\(\ \begin{align}M(z)=M_{B L} \quad \text { for } 1.0 \leq \zeta_*\tag{18.17b}\end{align}\)
where ζ* = 1 defines the top of the radix layer. In the bottom of the RxL, wind speed increases faster with height than given by the log wind profile for the neutral surface layer, but becomes tangent to the uniform winds MBL in the mid-mixed layer (Fig. 18.20).
The dimensionless height in the eqs. above is
\(\ \begin{align}\zeta_{*}=\frac{1}{C} \cdot \frac{z}{z_{i}} \cdot\left(\frac{w_{*}}{u_{*}}\right)^{B}\tag{18.18}\end{align}\)
where w* is the Deardorff velocity, and the empirical coefficients are A = 1/4, B = 3/4, and C = 1/2. D = 1/2 over flat terrain, but increases to near D = 1.0 over hilly terrain.
The Deardorff velocity (eq. 3.39) is copied here:
\(\ \begin{align}w_{*}=\left[\frac{|g|}{T_{v}} \cdot z_{i} \cdot F_{H S f c}\right]^{1 / 3}\tag{18.19a}\end{align}\)
where |g| = 9.8 m s–2 is gravitational acceleration magnitude, Tv is absolute virtual temperature, zi is depth of the ABL (= depth of the mixed layer), and FHsfc is the kinematic sensible heat flux (units of K·m s–1) at the surface. Typical values of w* are on the order of 1 m s–1. The Deardorff velocity and buoyancy velocity wB (defined in the Heat chapter) are both convective velocity scales for the statically unstable ABL, and are related by:
\(\ \begin{align}w_{*} \approx 0.08 w_{B}\tag{18.19b}\end{align}\)
To use eq. (18.17) you need to know the average wind speed in the middle of the mixed layer MBL, as was sketched in Fig. 18.9. The Atmos. Forces & Winds chapter shows how to estimate this if it is not known from measurements.
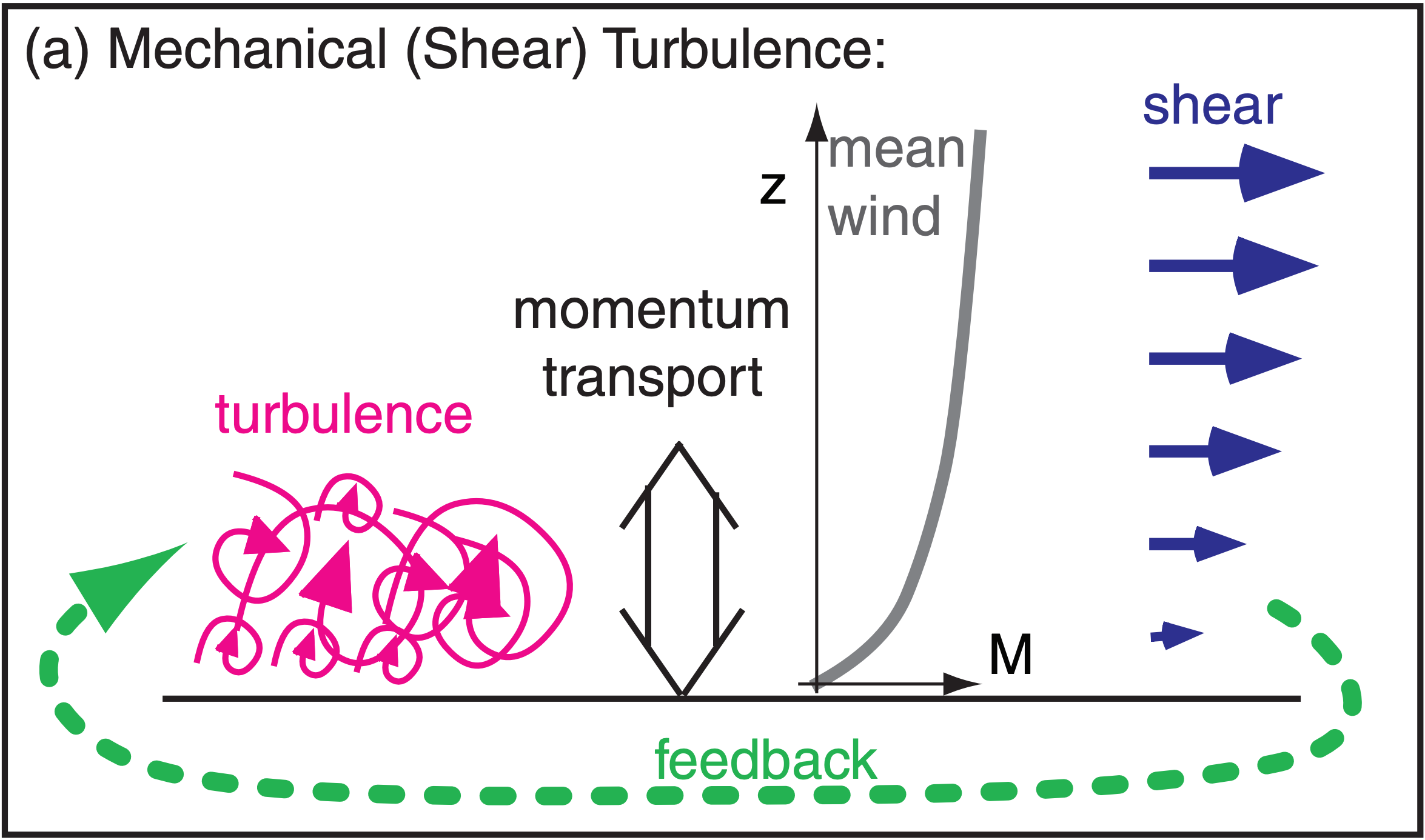
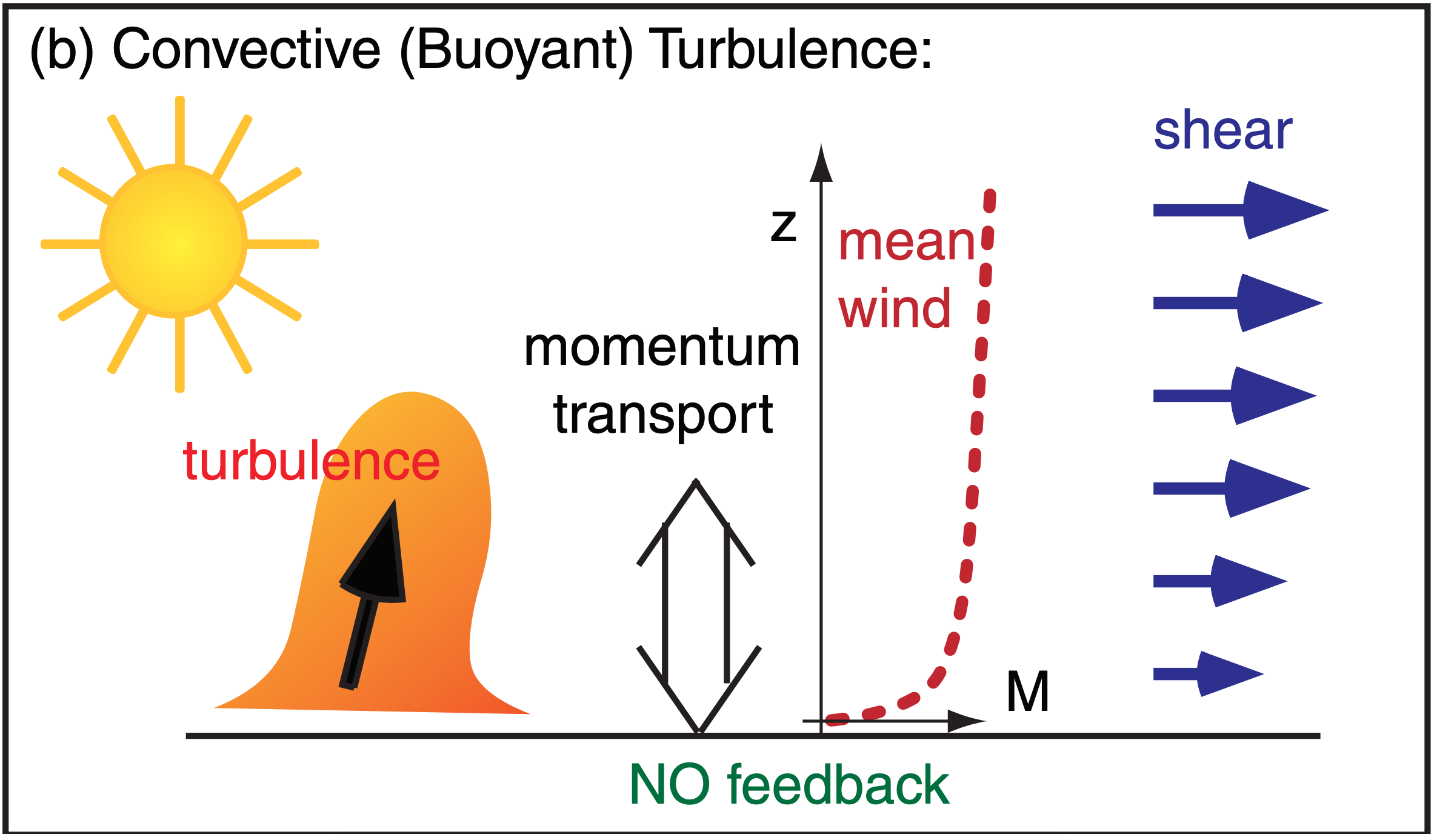
For both the free-convection radix layer and the forced-convection surface layer, turbulence transports momentum, which controls wind-profile shape, which then determines the shear (Fig. 18.22). However, differences in feedback lead to the difference between the radix layer and the surface layer.
In the neutral surface layer (Fig. 18.22a) there is strong feedback because wind shear generates the turbulence, which in turn controls the wind shear. However, such feedback is broken for convective turbulence (Fig. 18.22b), because it is generated primarily by buoyant thermals, not by shear.
Sample Application (§)
For a 1 km deep mixed layer with surface heat flux of 0.3 K·m s–1 and friction velocity of 0.2 m s–1, plot the wind speed profile using a spreadsheet. Terrain is flat, and mid-ABL wind is 5 m s–1.
Find the Answer
Given: FHsfc =0.3 K·m s–1, u* = 0.2 m s–1, zi = 1000 m, MBL = 5 m s–1, D = 0.5 .
Find: M(z) = ? m s–1.
The ABL is statically unstable, because FHsfc is positive.
First, find w* = ? m s–1 using eq. (18.19a).
Assume: |g|/Tv = 0.0333 m·s–2·K–1 (typical).
\(\ w_{*}=\left[\left(0.0333 \frac{\mathrm{m}}{\mathrm{s}^{2} \mathrm{K}}\right) \cdot(1000 \mathrm{m}) \cdot\left(0.3 \frac{\mathrm{K} \cdot \mathrm{m}}{\mathrm{s}}\right)\right]^{1 / 3}\)
= (10 m3 s–3) 1/3 = 2.15 m s–1
Use eq. (18.18) in a spreadsheet to get ζ* at each z, then use eq. (18.17) to get each M. For example, at z = 10 m:
ζ* = 2·(10m/1000m)·[(2.15m s–1)/(0.2m s–1)]3/4
= 0.1187 , &
M =(5m s–1)·(0.1191/2) 1/4·exp[0.25·(1– 0.1191/2)]
= 4.51m s–1
| z (m) | ζ* | M (m s–1) |
|---|---|---|
| 0 | 0.000 | 0.00 |
| 0.1 | 0.001 | 2.74 |
| 0.2 | 0.002 | 2.98 |
| 0.5 | 0.006 | 3.32 |
| 1.0 | 0.012 | 3.59 |
| 2 | 0.024 | 3.87 |
| 5 | 0.059 | 4.24 |
| 10 | 0.119 | 4.51 |
| 15 | 0.178 | 4.66 |
| 20 | 0.237 | 4.75 |
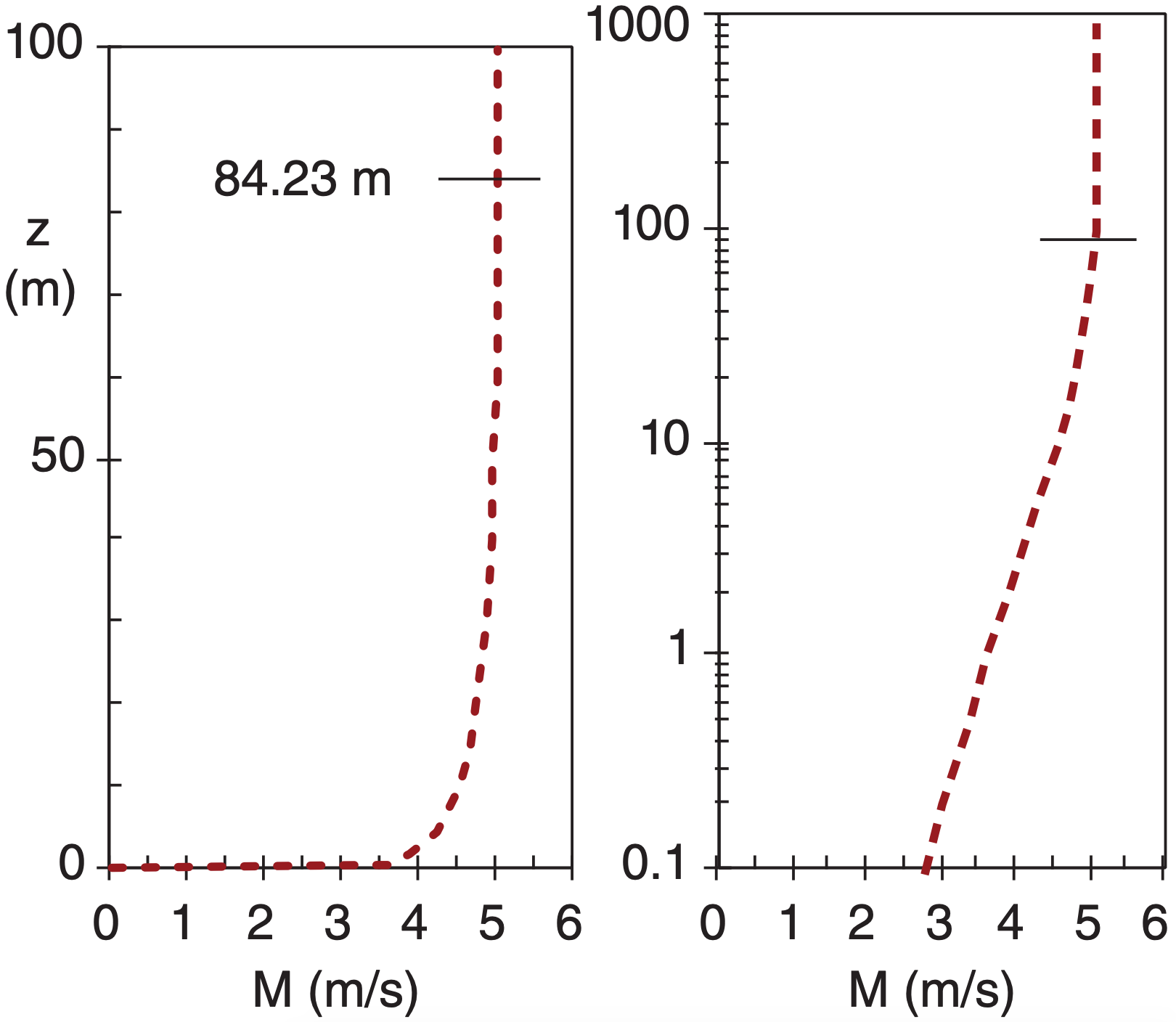
Check: Units OK. Physics OK. Sketch OK.
Exposition: This profile smoothly merges into the uniform wind speed in the mid-mixed layer, at height ζ* = 1.0, which is at z = C·zi ·(u*/w*)B = 84.23 m from eq. (18.18).


