17.6: Coastally Trapped Low-level (Barrier) Jets
- Page ID
- 9643
Coriolis force is also important in locations such as the eastern Pacific Ocean, where coastally trapped low-level wind jets form parallel to the west coast of N. America. Similar barrier jets can form at other mountain ranges. These jets have dynamics that are very similar to the dynamics of long-gap winds.
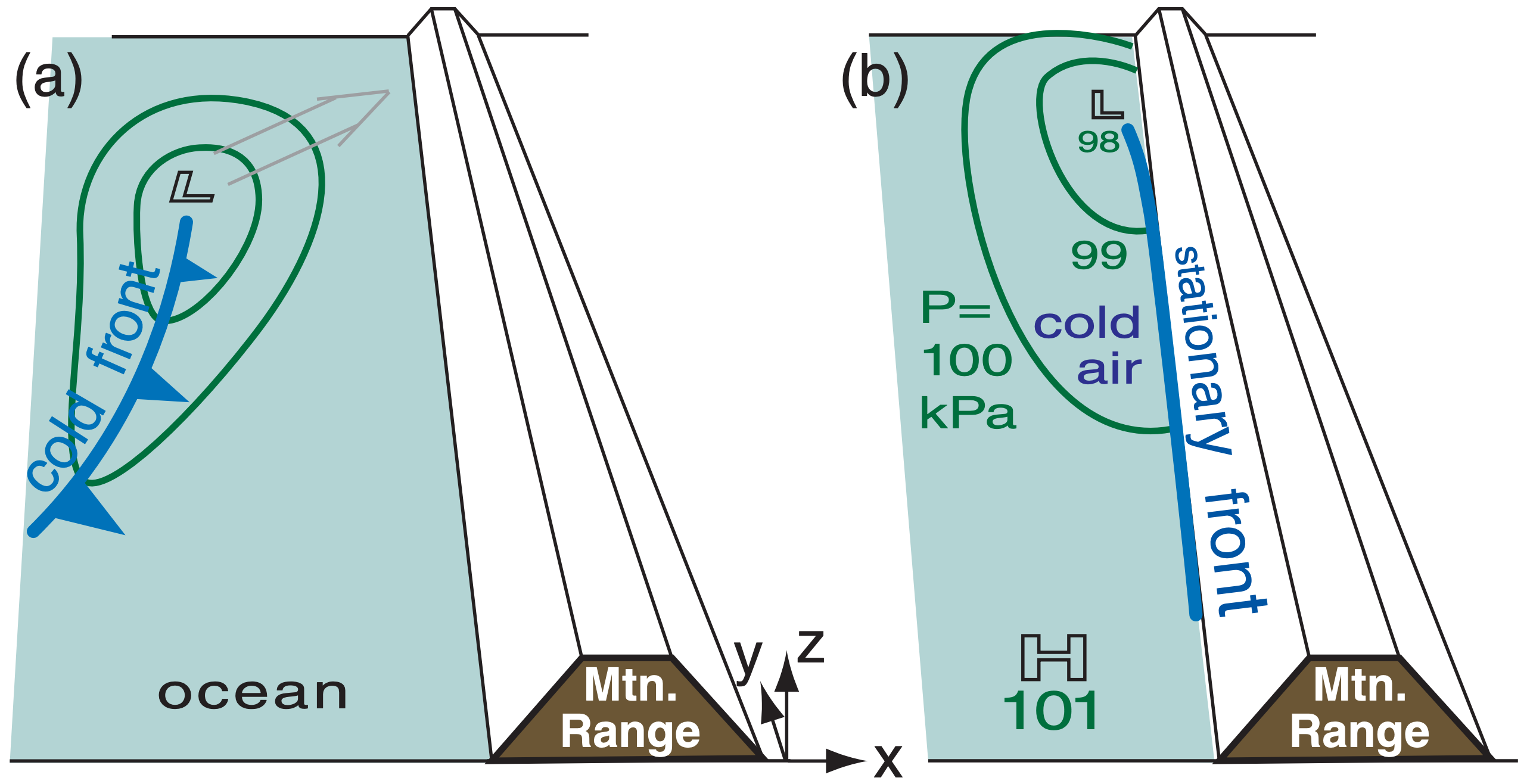
Consider situations where synoptic-scale lowpressure systems reach the coast of N. America and encounter mountain ranges. Behind the approaching cyclone is cold air, the leading edge of which is the cold front (Fig. 17.26a). The cold air stops advancing eastward when it hits the mountains, causing a stationary front along the ocean side of the mountain range (Fig. 17.26b).
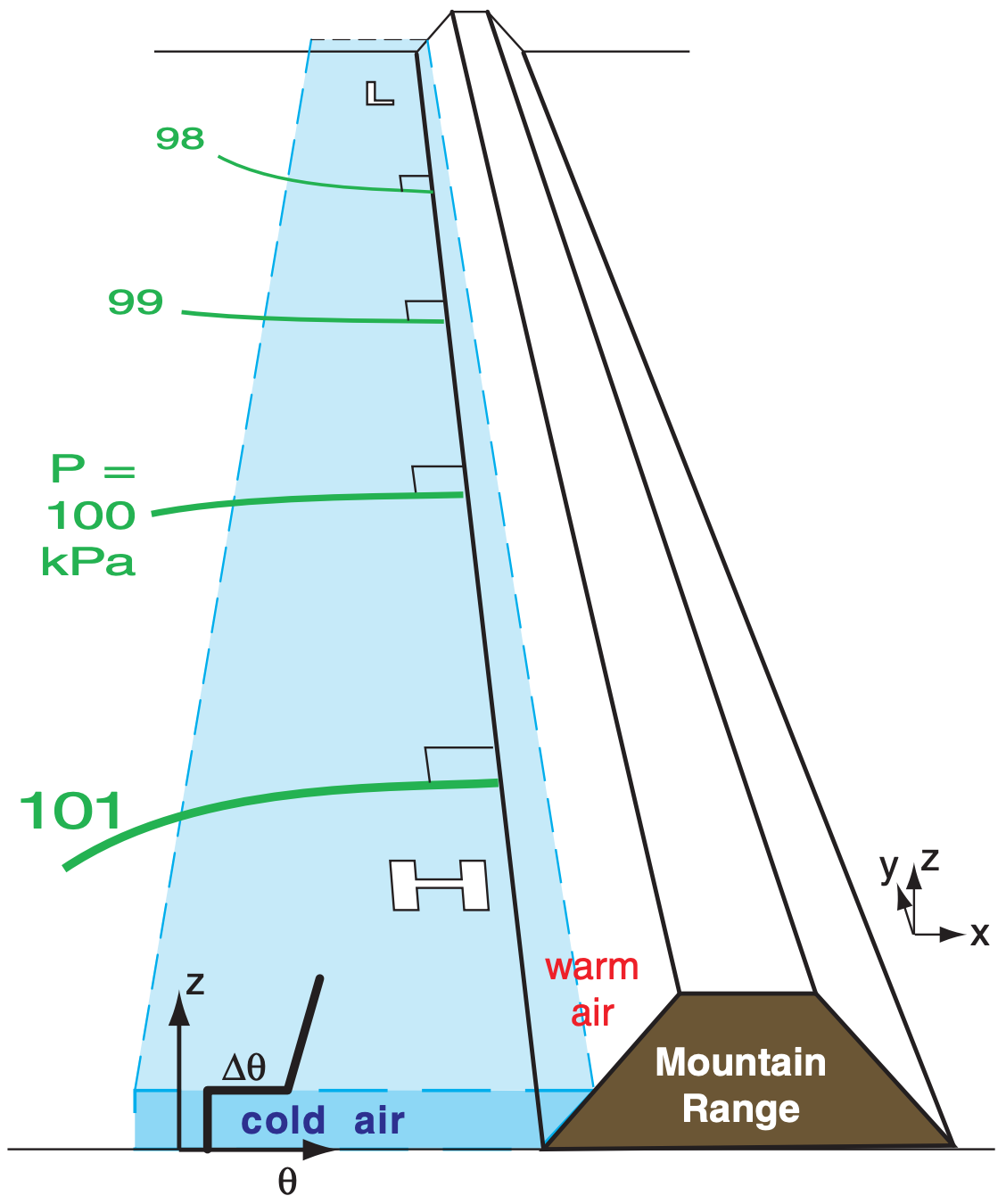
A pressure gradient forms parallel to the mountain range (Fig. 17.26b), between the low (L) center to the north and higher pressure (H) to the south. Fig. 17.27 shows a zoomed view of the resulting situation close to the mountains. The isobars are approximately perpendicular to the mountain-range axis, not parallel as was the case for gap winds.
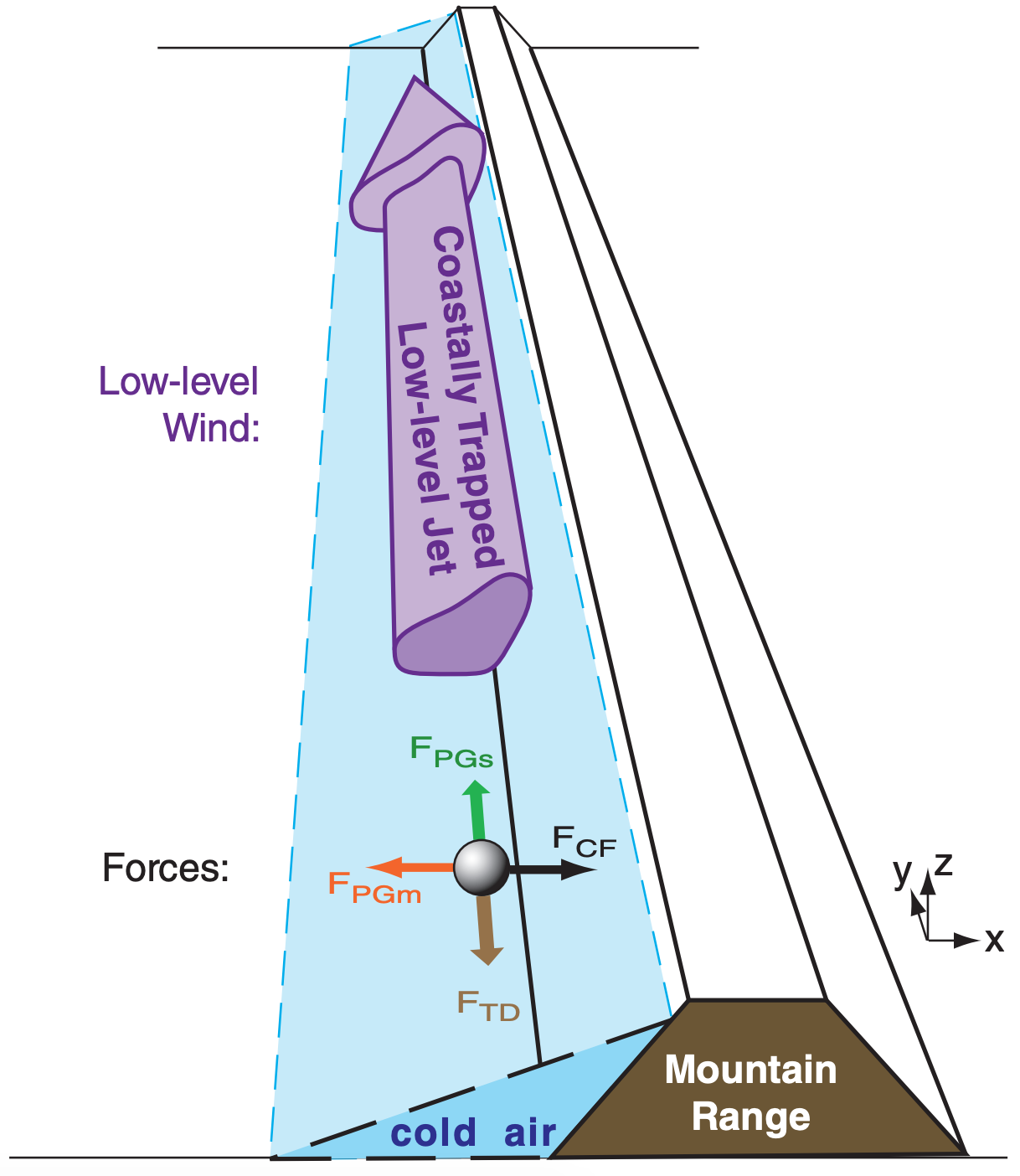
As the synoptic-scale pressure gradient (PGs) accelerates the cold air from high towards low, Coriolis force (CF) turns this air toward the right (in the N. Hem.) causing the cold air to ride up along the mountain range. This creates a mesoscale pressure gradient (PGm) pointing down the cold-air slope (Fig. 17.28). Eventually an equilibrium is reached where turbulent drag (TD) nearly balances the synoptic pressure-gradient force, and Coriolis force is balanced by the mesoscale pressure gradient.
The end result is a low-altitude cold wind parallel to the coast, just west of the mountain range. The jet-core height is located vertically about 1/3 of the distance from the ocean (or lowland floor) to the ridge top. Jet core altitudes of 50 to 300 m above sea level have been observed along the west coast of N. America, while altitudes of about 1 km have been observed for barrier jet cores in California west of the Sierra-Nevada mountain range. Maximum speeds of 10 to 25 m s–1 have been observed in the jet core.
Width of the coastal jet is on the order of 100 to 150 km. This width is roughly equal to the Rossby radius of deformation, λR, which is a measure of the upstream region of influence of the mountain range on a flow that is in geostrophic balance. For a cold marine layer of air capped by a strong inversion as sketched in Fig. 17.28, the external Rossby radius of deformation is
\(\ \begin{align} \lambda_{R}=\frac{\sqrt{|g| \cdot h \cdot \Delta \theta_{v} / T_{v}}}{f_{c}}\tag{17.28}\end{align}\)
where|g| = 9.8 m·s–2 is gravitational acceleration magnitude, h is mountain range height, fc is the Coriolis parameter, ∆θv is the jump of virtual potential temperature at the top of the marine air layer, and Tv is an average absolute virtual temperature of the air. For a statically-stable layer of air having a linear increase of potential temperature with height instead of a step discontinuity, an internal Rossby radius of deformation is
\(\ \begin{align} \lambda_{R}=\frac{N_{B V} \cdot h}{f_{c}}\tag{17.29}\end{align}\)
where NBV = [(|g|/Tv) · ∆θv/∆z] 1/2 is the Brunt-Väisälä frequency.
Sample Application
The influence of the coast mountains extends how far to the west of the coastline in Fig. 17.28? The cold air has virtual potential temperature 8°C colder than the neighboring warm air. The latitude is such that the Coriolis parameter is 10–4 s–1. Mountain height is 2000 m.
Find the Answer
Given: h = 2000 m, ∆θv = 8°C = 8 K, fc = 10–4 s–1.
Find: λR = ? km, external Rossby deformation radius
Assume: |g|/Tv = 0.03333 m·s–2·K–1
The region of influence extends a distance equal to the Rossby deformation radius. Thus, use eq. (17.28):
λR = [(0.03333 m·s–2·K–1)·(2000 m)·(8 K)]1/2 /(10–4 s–1) = 231,000 m = 231 km
Check: Units OK. Magnitude OK.
Exposition: Even before fronts and low-pressure centers hit the coastal mountains, the mountains are already influencing these weather systems hundreds of kilometers offshore.


