10.8: Consercation of Air Mass
- Page ID
- 10199
When you move along a path at constant distance R above Earth’s center, gravitational acceleration appears to change slightly due to your motion. The measured gravity |gobs| = |g| – ar , where:
\(a_{r}=2 \cdot \Omega \cdot \cos (\phi) \cdot U+\left(U^{2}+V^{2}\right) / R\)
The first term is the vertical component of Coriolis force (eq. 10.17e in the INFO box on p.297), and the last term is centrifugal force as you follow the curvature of the Earth. Thus, you feel lighter traveling east and heavier traveling west. This is the Eötvös effect.
Due to random jostling, air molecules tend to distribute themselves uniformly within any volume. Namely, the air tends to maintain its continuity. Any additional air molecules entering the volume that are not balanced by air molecules leaving (Fig. 10.26) will cause the air density (ρ, mass of air molecules in the volume) to increase, as described below by the continuity equation.
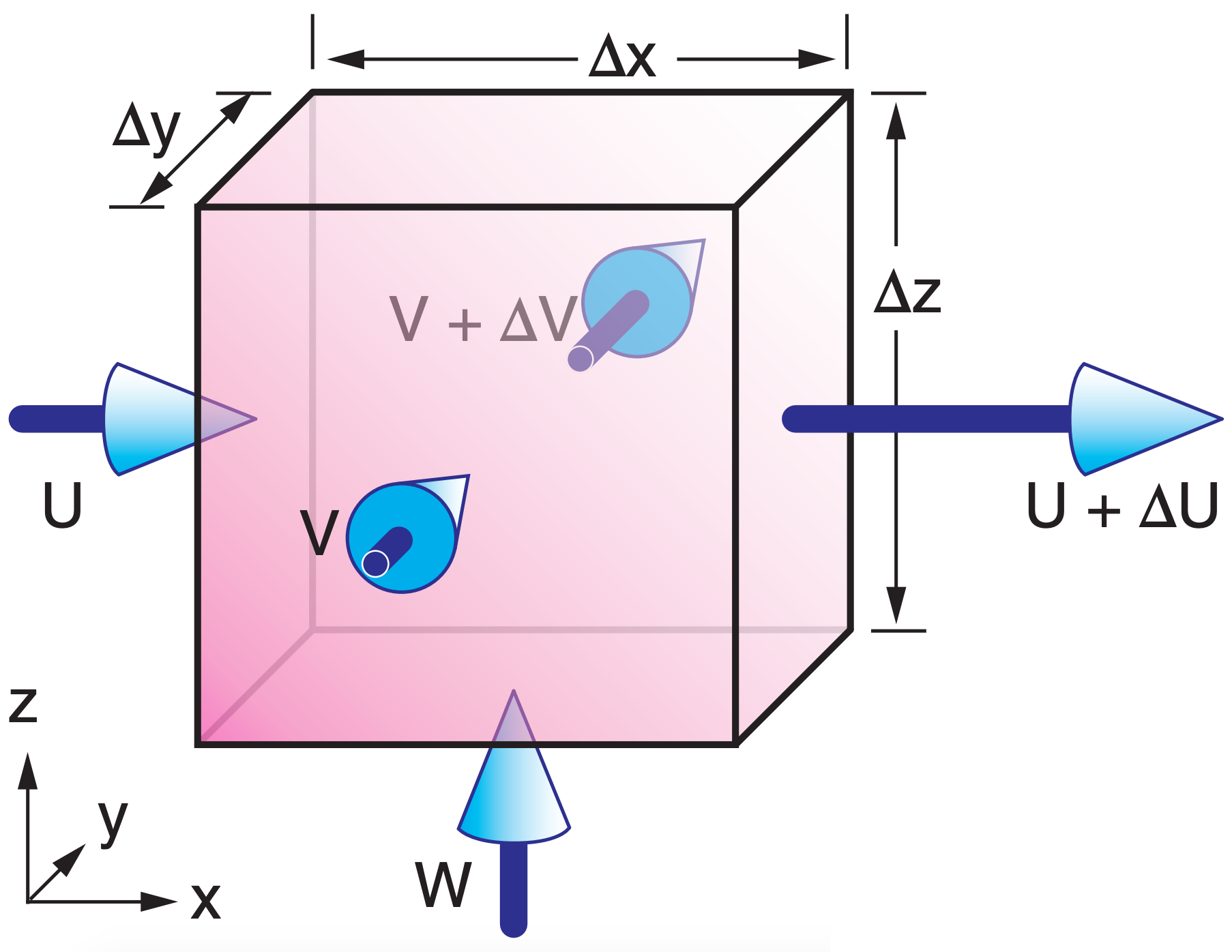
10.8.1. Continuity Equation
For a fixed Eulerian volume, the mass budget equation (i.e., the continuity equation) is:
\(\frac{\Delta \rho}{\Delta t}=\left\{-U \frac{\Delta \rho}{\Delta x}-V \frac{\Delta \rho}{\Delta y}-W \frac{\Delta \rho}{\Delta z}\right\}-\rho\left[\frac{\Delta U}{\Delta x}+\frac{\Delta V}{\Delta y}+\frac{\Delta W}{\Delta z}\right]\)
Sample Application
Hurricane-force winds of 60 m s–1 blow into an north-facing entrance of a 20 m long pedestrian tunnel. The door at the other end of the tunnel is closed. The initial air density in the tunnel is 1.2 kg m–3. Find the rate of air density increase in the tunnel.
Find the Answer
Given: VN. entrance = –60 m s–1, VS. entrance = 0 m s–1, ρ = 1.2 kg m–3, ∆ y = 20 m,
Find: ∆ρ/∆t = ? kg·m3·s–1 initially.
Use eq. (10.60), with U = W = 0 because the other walls, roof, and floor prevent winds in those directions:
\(\frac{\Delta \rho}{\Delta t}=-\rho \frac{V_{N, \text {entr.}}-V_{S, \text {entr.}}}{\Delta y_{\text {tunnel}}}=-\left(1.2 \frac{\mathrm{kg}}{\mathrm{m}^{3}}\right) \frac{(-60-0) \mathrm{m} / \mathrm{s}}{(20) \mathrm{m}}\)
∆ρ/∆t = +3.6 kg·m–3·s–1 .
Check: Physics & units are reasonable.
Exposition: As air density increases, so will air pressure. This pressure might be sufficient to blow open the other door at the south end of the pedestrian tunnel, allowing the density to decrease as air escapes.
The terms in curly braces { } describe advection. With a bit of calculus one can rewrite this equation as:
\(\ \begin{align} \frac{\Delta \rho}{\Delta t}=-\left[\frac{\Delta(\rho U)}{\Delta x}+\frac{\Delta(\rho V)}{\Delta y}+\frac{\Delta(\rho W)}{\Delta z}\right]\tag{10.61}\end{align}\)
where U, V, and W are the wind components in the x, y, and z directions, respectively, and t is time.
When you calculate wind gradients, be sure to take the wind and space differences in the same direction. For example: ∆U/∆x = (U2–U1)/(x2–x1).
10.8.2. Incompressible Idealization
Mean air density changes markedly with altitude, as was sketched in Fig. 10.25. However, at any one altitude the density changes only slightly due to local changes in humidity and temperature. For non-tornadic, non-thunderstorm conditions where Fig. 10.25 is valid, we can make a reasonable simplifying idealization that density is constant (∆ρ ≈ 0) at any one altitude. Namely, air behaves as if it is incompressible.
If we make this idealization, then the advection terms of eq. (10.60) are zero, and the time-tendency term is zero. The net result is volume conservation, where volume outflow equals volume inflow:
\(\ \begin{align} \frac{\Delta U}{\Delta x}+\frac{\Delta V}{\Delta y}+\frac{\Delta W}{\Delta z}=0\tag{10.62}\end{align}\)
Fig. 10.26 illustrates such incompressible continuity. Can you detect an error in this figure? It shows more air leaving the volume in each coordinate direction than is entering — impossible for incompressible flow. A correct figure would have changed arrow lengths, to indicate net inflow in one or two directions, balanced by net outflow in the other direction(s).
As will be explained in the last section of this chapter, divergence is where more air leaves a volume than enters (corresponding to positive terms in eq. 10.62). Convergence is where more air enters than leaves (corresponding to negative terms in eq. 10.62). Thus, volume (mass) conservation of incompressible flow requires one or two terms in eq. (10.62) to be negative (i.e., convergence), and the remaining term(s) to be positive (i.e., divergence) so that their sum equals zero.
Horizontal divergence (D) is defined as
\(\ \begin{align} D=\frac{\Delta U}{\Delta x}+\frac{\Delta V}{\Delta y}\tag{10.63}\end{align}\)
Negative values of D correspond to convergence. Plugging this definition into eq. (10.62) shows that vertical velocities increase with height where there is horizontal convergence:
\(\ \begin{align} \frac{\Delta W}{\Delta z}=-D\tag{10.64}\end{align}\)
10.8.3. Boundary-Layer Pumping
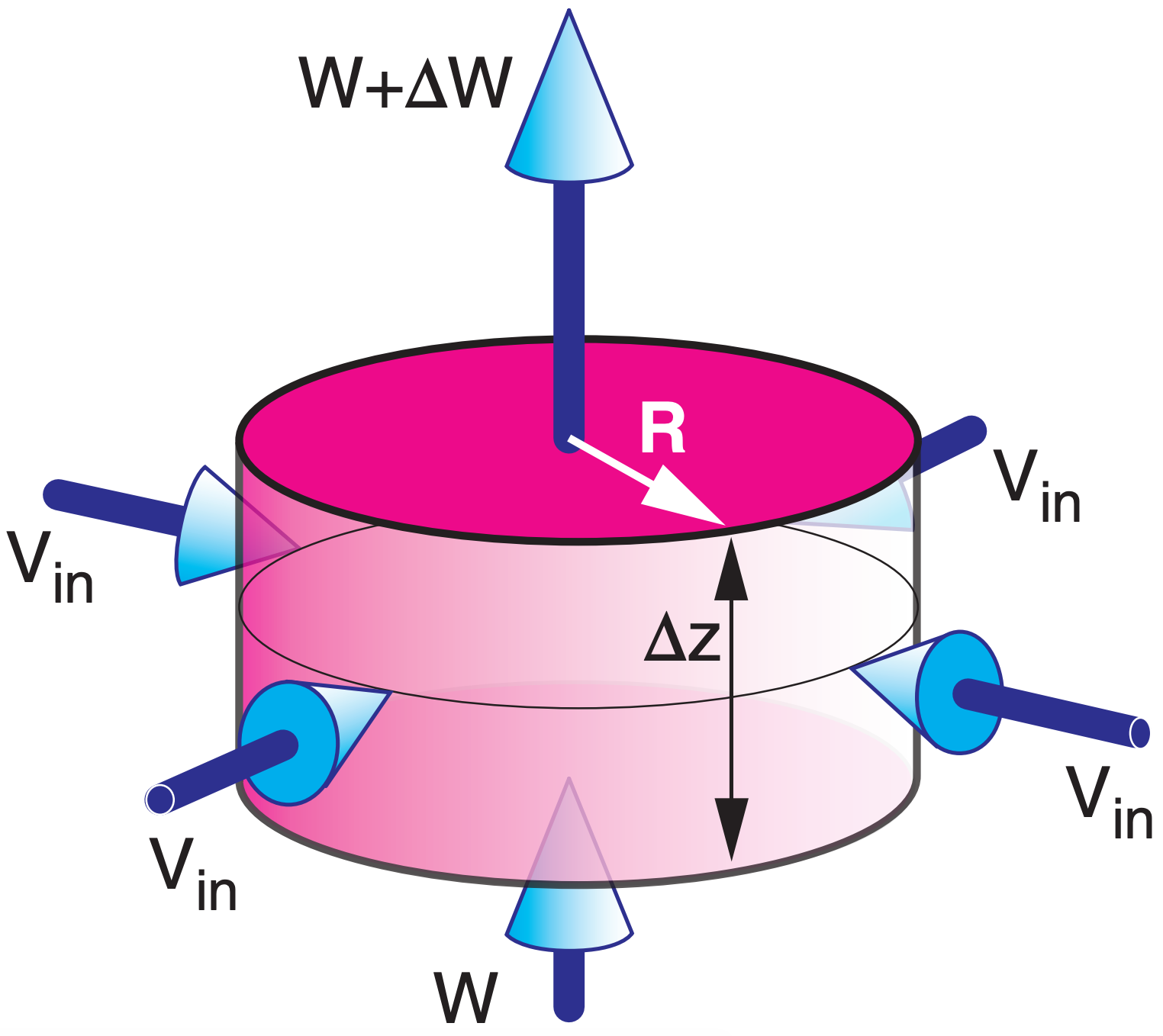
Consider an extratropical cyclone, where the boundary-layer gradient wind spirals in toward the low-pressure center. Those spiraling winds consist of a tangential component following the isobars as they encircle the low center, and a radial component having inflow velocity Vin (Fig. 10.27).
But volume inflow (2πR·∆z · Vin) through the sides of the cylindrical volume of radius R and height ∆z must be balanced by net volume outflow (πR2 · ∆W/∆z) through the top and bottom. Equating these incompressible flows gives:
\(\ \begin{align} \frac{2 \cdot V_{i n}}{R}=\frac{\Delta W}{\Delta z}\tag{10.65a}\end{align}\)
Thus, for horizontal inflow everywhere (positive Vin), one finds that ∆W must also be positive.
If a cylinder of air is at the ground where W = 0 at the cylinder bottom, then W at the cylinder top is:
\(\ \begin{align} W=\left(2 \cdot V_{i n} \cdot \Delta z\right) / R\tag{10.65b}\end{align}\)
Namely, extratropical cyclones have rising air, which causes clouds and rain due to adiabatic cooling. This forcing of a broad updraft region by horizontal-wind drag around a cyclone is known as boundary-layer pumping or Ekman pumping.
For atmospheric boundary-layer gradient (ABLG) winds around anticyclones (highs), the opposite occurs: horizontal outflow and a broad region of descending air (subsidence). The subsidence causes adiabatic warming, which evaporates any clouds and creates fair weather.
Recall from the ABLG wind section that an analytical solution could not be found for VABLG (which is the needed Vin for eq. 10.65). Instead, we can approximate Vin ≈ VABL for which an analytical solution exists. But VABL is always larger than VABLG for flow around cyclones, so we must be aware that our analytical answer will always give winds that are slightly faster than occur around lows in nature.
To solve for VABL, we need to make an assumption about the static stability of the atmospheric boundary layer. Because cyclones generally have overcast skies and strong winds, we can safely assume neutral stability. In this case, eq. (10.41b) gives the cross-isobaric inflow velocity.
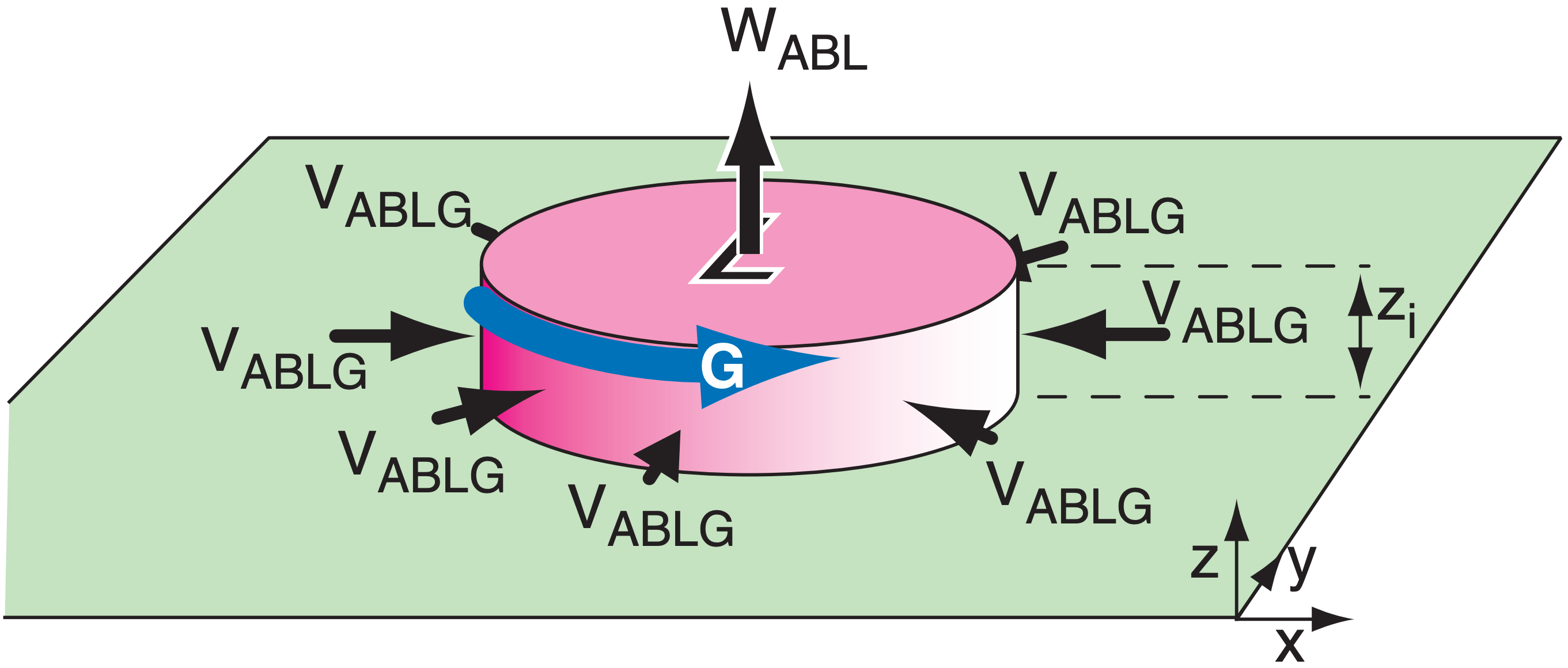
Use VABL for Vin in eq. (10.65b) and solve for W (which we will call WABL — the vertical velocity at the atmospheric boundary-layer top, as sketched in Fig. 10.28):
\(\ \begin{align} W_{A B L}=\frac{2 \cdot b \cdot C_{D}}{f_{c}} \cdot \frac{G^{2}}{R}\tag{10.66}\end{align}\)
with geostrophic wind G, radius of curvature R, Coriolis parameter fc, and drag coefficient CD for statically neutral boundary conditions. For flow over land, CD ≈ 0.005 .
Eq. (10.41b) can be used to find b = { 1 – 0.5·[CD·G/ (fc·zi )] } for an atmospheric boundary layer of thickness zi . If you don’t know the actual atmospheric boundary-layer depth, then a crude approximation for cyclones (not valid for anticyclones) is :
\(\ \begin{align} z_{i} \approx \frac{G}{N_{B V}}\tag{10.67}\end{align}\)
In this approximation, you must use a Brunt-Väisälä frequency NBV that is valid for the statically stable air in the troposphere above the top of the statically neutral atmospheric boundary layer. For this special approximation: b = { 1 – 0.5·[CD·NBV/fc]}. A required condition for a physically realistic solution is [CD·NBV/fc] < 1.
You can interpret eq. (10.66) as follows. Stronger pressure gradients (which cause larger geostrophic wind G), larger drag coefficients, and smaller radii of curvature cause greater atmospheric boundarylayer pumping WABL.
Although the equations above allow a complete approximate solution, we can rewrite them in terms of a geostrophic relative vorticity:
\(\ \begin{align} \zeta_{g}=\frac{2 \cdot G}{R}\tag{10.68}\end{align}\)
which indicates air rotation. Vorticity is introduced later in this chapter, and is covered in greater detail in the General Circulation chapter.
Eq. (10.66) can be modified to use geostrophic vorticity. The resulting Ekman pumping at the atmospheric boundary layer top in a midlatitude cyclone is:
\(\ \begin{align} W_{A B L}=C_{D} \cdot \frac{G}{f_{c}} \cdot \zeta_{g} \cdot\left[1-0.5 \frac{C_{D} \cdot N_{B V}}{f_{c}}\right]\tag{10.69}\end{align}\)
The first four factors on the right side imply that larger drag coefficients (i.e., rougher terrain with more trees or buildings) and stronger pressure gradients (as indicated by larger geostrophic wind) driving winds around smaller radii of curvature (i.e., larger geostrophic vorticity) at lower latitudes (i.e., smaller fc) create stronger updrafts. Also, stronger static stabilities (i.e., larger Brunt-Väisälä frequency NBV) in the troposphere above atmospheric boundary-layer top reduce updraft speed by opposing vertical motion.
One can write an internal Rossby deformation radius based on the eq. (10.67) approximation for depth zi of the atmospheric boundary layer:
\(\ \begin{align} \lambda_{R} \approx \frac{G}{f_{c}} \cdot \frac{z_{T}}{z_{i}}\tag{10.70}\end{align}\)
where tropospheric depth is zT. Internal and external Rossby deformation radii are described further in the General Circulation and Fronts & Airmasses chapters, respectively
The Rossby deformation radius can be used to write yet another expression for Ekman pumping vertical velocity out of the top of the atmospheric boundary layer:
\(\ \begin{align} W_{A B L}=C_{D} \cdot \frac{z_{i}}{z_{T}} \cdot \lambda_{R} \cdot \zeta_{g} \cdot\left[1-0.5 \cdot \mathrm{C}_{D} \cdot \frac{\lambda_{R}}{z_{T}}\right]\tag{10.71}\end{align}\)
Sample Application
At 500 km from the center of a midlatitude cyclone at latitude where fc = 0.0001 s–1, the pressure gradient can drive a 15 m s–1 geostrophic wind. Assume a standard atmosphere static stability above the top of the atmospheric boundary layer (ABL), and a drag coefficient of 0.004 at the bottom. Find the Ekman pumping updraft speed out of the atmospheric boundary-layer top. Also, what are the geostrophic relative vorticity, the depth of the ABL, and the internal Rossby deformation radius?
Find the Answer
Given: fc = 0.0001 s–1, R = 5x105 m, G = 15 m s–1, CD = 0.004,
Find: WABL = ? m s–1, ζg = ? s–1, zi = ? m, λR = ? km
For depth of the troposphere, assume zT = 11 km.
First, to get the Brunt-Väisälä frequency, use the Standard-Atmosphere temperatures (see Chapter 1) at the top and bottom of the troposphere to estimate the average temperature and vertical temperature gradient:
Tavg = 0.5·(–56.5 + 15.0) = –20.8°C = 252K
∆T = (–56.5 – 15.0)°C = –71.5°C across ∆z = 11 km
Use these in eq (5.4a):
\(N_{B V}=\sqrt{\frac{9.8 \mathrm{m} / \mathrm{s}}{252 \mathrm{K}}\left[\frac{-71.5 \mathrm{K}}{11000 \mathrm{m}}+0.0098 \frac{\mathrm{K}}{\mathrm{m}}\right]}=0.0113 \mathrm{s}^{-1}\)
Apply eq. (10.67):
zi ≈ G/NBV = (15 m s–1)/(0.0113 s–1) = 1327 m
Apply eq. (10.68):
\(\zeta_{g}=\frac{2 \cdot(15 \mathrm{m} / \mathrm{s})}{5 \times 10^{5} \mathrm{m}}=\underline{6 \times 10^{-5} \mathrm{s}^{-1}}\)
Apply eq. (10.70):
\(\lambda_{R} \approx \frac{(15 \mathrm{m} / \mathrm{s})}{\left(0.0001 \mathrm{s}^{-1}\right)} \cdot \frac{11 \mathrm{km}}{1.327 \mathrm{km}}=1243 \mathrm{km}\)
We need to check to ensure that [CD·NBV/fc] < 1.
[0.004·(0.0113s–1)/(0.0001s–1)] = 0.452 < 1.
Thus, we can expect our approximate solution should work for this case.
Apply eq. (10.71): WABL = \(0.004 \cdot \frac{(1.327 \mathrm{km})}{(11 \mathrm{km})} \cdot\left(1.243 \times 10^{6} \mathrm{m}\right) \cdot\left(6 \times 10^{-5} \mathrm{s}^{-1}\right)
\cdot\left[1-0.5 \cdot(0.004) \cdot \frac{1243 \mathrm{km}}{11 \mathrm{km}}\right]
=\left(0.036 \mathrm{m} \mathrm{s}^{-1}\right) \cdot[0.774]=0.028 \mathrm{m} \mathrm{s}^{-1}\)
Check: Physics and units are reasonable.
Exposition: The updraft speed 2.8 cm s–1 is slow, but over many hours can cause significant lifting. As the rising air cools adiabatically, clouds form and latent heat is released due to condensation. Hence, clouds and bad weather are often associated with midlatitude cyclones.


