10.3: Horizontal Forces
- Page ID
- 9591
Five forces contribute to net horizontal accelerations that control horizontal winds: pressure-gradient force (PG), advection (AD), centrifugal force (CN), Coriolis force (CF), and turbulent drag (TD):
\(\ \begin{align} \frac{F_{x\ n e t}}{m}=\frac{F_{x\ A D}}{m}+\frac{F_{x\ P G}}{m}+\frac{F_{x\ C N}}{m}+\frac{F_{x\ C F}}{m}+\frac{F_{x\ T D}}{m}\tag{10.7a}\end{align}\)
\(\ \begin{align} \frac{F_{y\ n e t}}{m}=\frac{F_{y\ A D}}{m}+\frac{F_{y\ P G}}{m}+\frac{F_{y\ C N}}{m}+\frac{F_{y\ C F}}{m}+\frac{F_{y\ T D}}{m}\tag{10.7b}\end{align}\)
Centrifugal force is an apparent force that allows us to include inertial effects for winds that move in a curved line. Coriolis force, explained in detail later, includes the gravitational and compound centrifugal forces on a non-spherical Earth. In the equations above, force per unit mass has units of N kg–1. These units are equivalent to units of acceleration (m·s–2 , see Appendix A), which we will use here.
10.3.1. Advection of Horizontal Momentum
Advection is not a true force. Yet it can cause a change of wind speed at a fixed location in Eulerian coordinates, so we will treat it like a force here. The wind moving past a point can carry specific momentum (i.e., momentum per unit mass). Recall that momentum is defined as mass times velocity, hence specific momentum equals the velocity (i.e., the wind) by definition. Thus, the wind can move (advect) different winds to your fixed location.
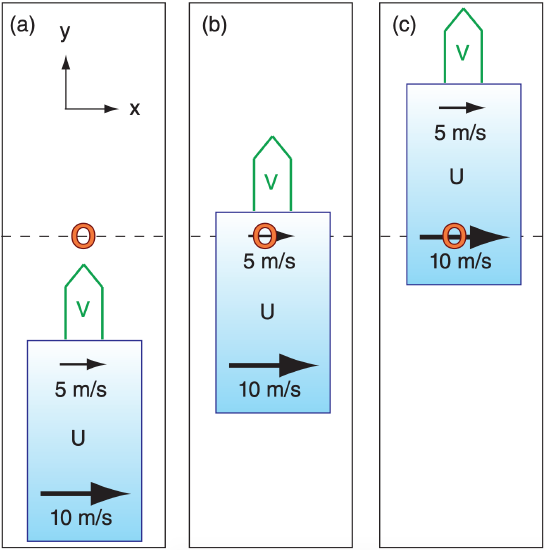
This is illustrated in Fig. 10.4a. Consider a mass of air (grey box) with slow U wind (5 m s–1) in the north and faster U wind (10 m s–1) in the south. Thus, U decreases toward the north, giving ∆U/∆y = negative. This whole air mass is advected toward the north over a fixed weather station “O” by a south wind (V = positive). At the later time sketched in Fig. 10.4b, a west wind of 5 m s–1 is measured at “O”. Even later, at the time of Fig. 10.4c, the west wind has increased to 10 m s–1 at the weather station. The rate of increase of U at “O” is larger for faster advection (V), and when ∆U/∆y is more negative.
Thus, ∆U/∆t = –V · ∆U/∆y for this example. The advection term on the RHS causes an acceleration of U wind on the LHS, and thus acts like a force per unit mass: ∆U/∆t = Fx AD/m = –V · ∆U/∆y .
You must always include advection when momentum-budget equations are written in Eulerian frameworks. This is similar to the advection terms in the moisture- and heat-budget Eulerian equations that were in earlier chapters.
For advection, the horizontal force components are
\(\ \begin{align} \frac{F_{x\ A D}}{m}=-U \cdot \frac{\Delta U}{\Delta x}-V \cdot \frac{\Delta U}{\Delta y}-W \cdot \frac{\Delta U}{\Delta z}\tag{10.8a}\end{align}\)
\(\ \begin{align}\frac{F_{y\ A D}}{m}=-U \cdot \frac{\Delta V}{\Delta x}-V \cdot \frac{\Delta V}{\Delta y}-W \cdot \frac{\Delta V}{\Delta z}\tag{10.8b}\end{align}\)
Recall that a gradient is defined as change across a distance, such as ∆V/∆y. With no gradient, the wind cannot cause accelerations.
Vertical advection of horizontal wind (–W·∆U/∆z in eq. 10.8a, and –W·∆V/∆z in eq. 10.8b) is often very small outside of thunderstorms.
Sample Application
Minneapolis (MN, USA) is about 400 km north of Des Moines (IA, USA). In Minneapolis the wind components (U, V) are (6, 4) m s–1 , while in Des Moines they are (2, 10) m s–1. What is the value of the advective force per mass?
Find the Answer
Given: (U, V) = (6, 4) m s–1 in Minneapolis, (U, V) = (2, 10) m s–1 in Des Moines ∆y = 400 km, ∆x = is not relevant
Find: Fx AD/m =? m·s–2 , Fy AD/m =? m·s–2
Use the definition of a gradient:
∆U/∆y = (6 – 2 m s–1)/400,000 m = 1.0x10–5 s–1
∆U/∆x = not relevant, ∆U/∆z = not relevant,
∆V/∆y = (4 – 10 m s–1)/400,000 m = –1.5x10–5 s–1
∆V/∆x = not relevant, ∆V/∆z = not relevant
Average U = (6 + 2 m s–1)/2 = 4 m s–1
Average V = (4 + 10 m s–1)/2 = 7 m s–1
Use eq. (10.8a):
Fx AD/m = – (7m s–1)·(1.0x10–5 s–1 ) = –7x10–5 m·s–2
Use eq. (10.8b):
Fy AD/m = – (7m s–1)·(–1.5x10–5 s–1 ) = 1.05x10–4 m·s–2
Check: Physics and units are reasonable.
Exposition: The slower U winds from Des Moines are being blown by positive V winds toward Minneapolis, causing the U wind speed to decrease at Minneapolis. But the V winds are increasing there because of the faster winds in Des Moines moving northward.
10.3.2. Horizontal Pressure-Gradient Force
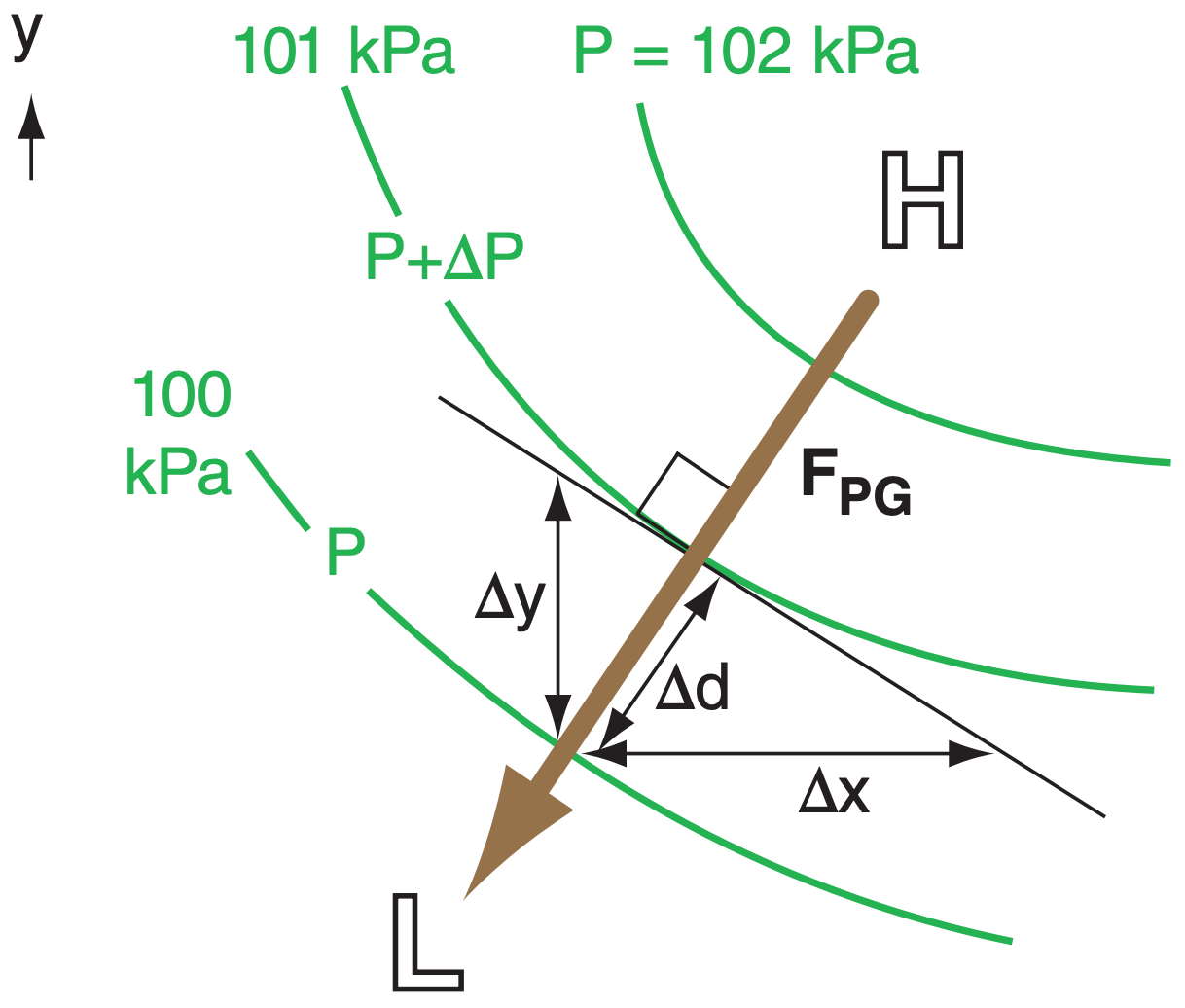
In regions where the pressure changes with distance (i.e., a pressure gradient), there is a force from high to low pressure. On weather maps, this force is at right angles to the height contours or isobars, directly from high heights or high pressures to low. Greater gradients (shown by a tighter packing of isobars; i.e., smaller spacing ∆d between isobars on weather maps) cause greater pressure-gradient force (Fig. 10.5). Pressure-gradient force is independent of wind speed, and thus can act on winds of any speed (including calm) and direction.
For pressure-gradient force, the horizontal components are:
\(\ \begin{align}\frac{F_{x P G}}{m}=-\frac{1}{\rho} \cdot \frac{\Delta P}{\Delta x}\tag{10.9a}\end{align}\)
\(\ \begin{align} \frac{F_{y P G}}{m}=-\frac{1}{\rho} \cdot \frac{\Delta P}{\Delta y}\tag{10.9b}\end{align}\)
where ∆P is the pressure change across a distance of either ∆x or ∆y, and ρ is the density of air.
Sample Application
Minneapolis (MN, USA) is about 400 km north of Des Moines (IA, USA). In (Minneapolis , Des Moines) the pressure is (101, 100) kPa. Find the pressure-gradient force per unit mass? Let ρ = 1.1 kg·m–3.
Find the Answer
Given: P =101 kPa @ x = 400 km (north of Des Moines). P =100 kPa @ x = 0 km at Des Moines. ρ = 1.1 kg·m–3.
Find: Fy PG/m = ? m·s–2
Apply eq. (10.9b):
\(\frac{F_{y P G}}{m}=-\frac{1}{\left(1.1 \mathrm{kg} \cdot \mathrm{m}^{-3}\right)} \cdot \frac{(101,000-100,000) \mathrm{Pa}}{(400,000-0) \mathrm{m}}\)
= –2.27x10–3 m·s–2.
Hint, from Appendix A: 1 Pa = 1 kg·m–1·s–2.
Check: Physics and units are reasonable.
Exposition: The force is from high pressure in the north to low pressure in the south. This direction is indicated by the negative sign of the answer; namely, the force points in the negative y direction.
If pressure increases toward one direction, then the force is in the opposite direction (from high to low P); hence, the negative sign in these terms. Pressure-gradient-force magnitude is
\(\ \begin{align} \left|\frac{F_{P G}}{m}\right|=\left|\frac{1}{\rho} \cdot \frac{\Delta P}{\Delta d}\right|\tag{10.10}\end{align}\)
where ∆d is the distance between isobars.
Eqs. (10.9) can be rewritten using the hydrostatic eq. (1.25) to give the pressure gradient components as a function of spacing between height contours on an isobaric surface:
\(\ \begin{align} \frac{F_{x P G}}{m}=-|g| \cdot \frac{\Delta z}{\Delta x}\tag{10.11a}\end{align}\)
\(\ \begin{align} \frac{F_{y P G}}{m}=-|g| \cdot \frac{\Delta z}{\Delta y}\tag{10.11b}\end{align}\)
for a gravitational acceleration magnitude of |g| = 9.8 m·s–2 . ∆z is the height change in the ∆x or ∆y directions; hence, it is the slope of the isobaric surface. Extending this analogy of slope, if you conceptually place a ball on the isobaric surface, it will roll downhill (which is the pressure-gradient force direction). The magnitude of pressure-gradient force is
\(\ \begin{align} \left|\frac{F_{P G}}{m}\right|=\left|g \cdot \frac{\Delta z}{\Delta d}\right|\tag{10.12}\end{align}\)
where ∆d is distance between height contours.
The one force that makes winds blow in the horizontal is pressure-gradient force. All the other forces are a function of wind speed, hence they can only change the speed or direction of a wind that already exists. The only force that can start winds blowing from zero (calm) is pressure-gradient force.
Sample Application
If the height of the 50 kPa pressure surface decreases by 10 m northward across a distance of 500 km, what is the pressure-gradient force?
Find the Answer
Given: ∆z = –10 m, ∆y = 500 km, |g|= 9.8 m·s–2 .
Find: FPG/m = ? m·s–2
Use eqs. (10.11a & b):
Fx PG/m = 0 m·s–2 , because ∆z/∆x = 0. Thus, FPG/m = Fy PG/m.
\(\frac{F_{y P G}}{m}=-|g| \cdot \frac{\Delta z}{\Delta y}=-\left(9.8 \frac{\mathrm{m}}{\mathrm{s}^{2}}\right) \cdot\left(\frac{-10 \mathrm{m}}{500,000 \mathrm{m}}\right)\)
FPG/m = 0.000196 m·s–2.
Check: Physics, units & sign are reasonable.
Exposition: For our example here, height decreases toward the north, thus a hypothetical ball would roll downhill toward the north. A northward force is in the positive y direction, which explains the positive sign of the answer.
10.3.3. Centrifugal Force
Inertia makes an air parcel try to move in a straight line. To get its path to turn requires a force in a different direction. This force, which pulls toward the inside of the turn, is called centripetal force. Centripetal force is the result of a net imbalance of (i.e., the nonzero vector sum of) other forces.
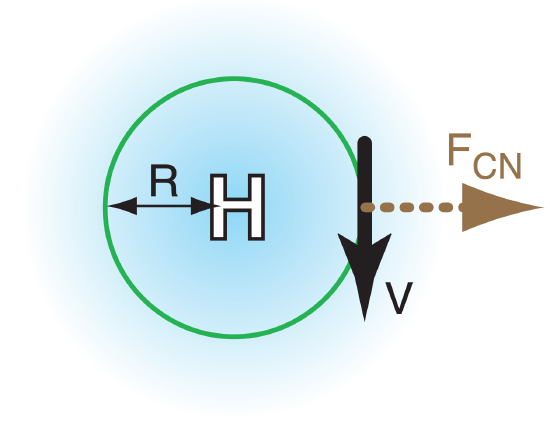
For mathematical convenience, we can define an apparent force, called centrifugal force, that is opposite to centripetal force. Namely, it points outward from the center of rotation. Centrifugal-force components are:
\(\ \begin{align} \frac{F_{x\ C N}}{m}=+s \cdot \frac{V \cdot M}{R}\tag{10.13a}\end{align}\)
\(\ \begin{align} \frac{F_{y\ C N}}{m}=-s \cdot \frac{U \cdot M}{R}\tag{10.13b}\end{align}\)
where M = ( U2 + V2 )1/2 is wind speed (always positive), R is radius of curvature, and s is a sign factor from Table 10-2 as determined by the hemisphere (North or South) and synoptic pressure center (Low or High).
Centrifugal force magnitude is proportional to wind speed squared:
\(\ \begin{align} \left|\frac{F_{C N}}{m}\right|=\frac{M^{2}}{R}\tag{10.14}\end{align}\)
| Table 10-2. To apply centrifugal force to separate Cartesian coordinates, a (+/–) sign factor s is required. | ||
| Hemisphere | For winds encircling a | |
| Low Pressure Center | High Pressure Center | |
| Southern | –1 | +1 |
| Northern | +1 | –1 |
Sample Application
500 km east of a high-pressure center is a north wind of 5 m s–1. Assume N. Hemisphere. What is the centrifugal force?
Find the Answer
Given: R = 5x105 m, U = 0, V = – 5 m s–1
Find: Fx CN/m = ? m·s–2.
Apply eq. (10.13a). In Table 10-2 find s = –1.
\(\frac{F_{x\ C N}}{m}=-1 \cdot \frac{(-5 \mathrm{m} / \mathrm{s}) \cdot(5 \mathrm{m} / \mathrm{s})}{5 \times 10^{5}}=5 \times 10^{-5} \mathrm{m} \cdot \mathrm{s}^{-2}\)
Check: Physics and units OK. Agrees with sketch.
Exposition: To maintain a turn around the high-pressure center, other forces (the sum of which is the centripetal force) are required to pull toward the center.
10.3.4. Coriolis Force
An object such as an air parcel that moves relative to the Earth experiences a compound centrifugal force based on the combined tangential velocities of the Earth’s surface and the object. When combined with the non-vertical component of gravity, the result is called Coriolis force (see the INFO box on the next page). This force points 90° to the right of the wind direction in the Northern Hemisphere (Fig. 10.6), and 90° to the left in the S. Hemisphere.
The Earth rotates one full revolution (2π radians) during a sidereal day (i.e., relative to the fixed stars, Psidereal is a bit less than 24 h, see Appendix B), giving an angular rotation rate of
\(\ \begin{align} \Omega=2 \cdot \pi / P_{\text {sidereal }}\tag{10.15}\end{align}\)
= 0.729 211 6 x 10–4 radians s–1
The units for Ω are often abbreviated as s–1. Using this rotation rate, define a Coriolis parameter as:
\(\ \begin{align} f_{c}=2 \cdot \Omega \cdot \sin (\phi)\tag{10.16}\end{align}\)
where ϕ is latitude, and 2·Ω = 1.458423x10–4 s–1. Thus, the Coriolis parameter depends only on latitude. Its magnitude is roughly 1x10–4 s–1 at mid-latitudes.
The Coriolis force in the Northern Hemisphere is:
\(\ \begin{align}\frac{F_{x\ C F}}{m}=f_{c} \cdot V\tag{10.17a}\end{align}\)
\(\ \begin{align}\frac{F_{y\ C F}}{m}=-f_{c} \cdot U\tag{10.17b}\end{align}\)
In the Southern Hemisphere the signs on the right side of eqs. (10.17) are opposite. Coriolis force is zero under calm conditions, and thus cannot create a wind. However, it can change the direction of an existing wind. Coriolis force cannot do work, because it acts perpendicular to the object’s motion.
The magnitude of Coriolis force is:
\(\ \begin{align} \left|F_{\mathrm{CF}} / m\right| \approx 2 \cdot \Omega \cdot|\sin (\phi) \cdot M|\tag{10.18a}\end{align}\)
or
\(\ \begin{align} \left|F_{\mathrm{CF}} / m\right| \approx\left|f_{\mathrm{c}} \cdot M\right|\tag{10.18b}\end{align}\)
Sample Application (§)
a) Plot Coriolis parameter vs. latitude.
b) Find FCF/m at Paris, given a north wind of 15 m s–1.
Find the Answer:
a) Given: ϕ = 48.874°N at Paris.
Find fc (s–1) vs. ϕ(°) using eq. (10.16). For example:
fc = (1.458x10–4 s–1)·sin(48.874°) = 1.1x10–4 s–1.
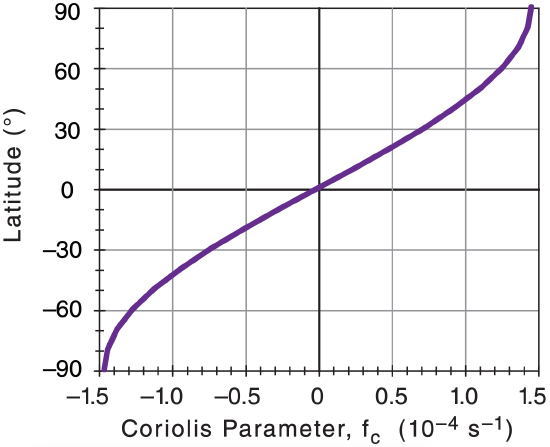
b) Given: V = –15 m s–1 . Find: FCF/m= ? m s–2
Assume U = 0 because no info, thus Fy CF/m= 0.
Apply eq. (10.17a):
Fx CF/m = (1.1x10–4 s–1)·(–15 m s–1) = –1.65x10–3 m s–2
Exposition: This Coriolis force points to the west.
Eqs. (10.17) give only the dominant components of Coriolis force. There are other smaller-magnitude Coriolis terms (labeled small below) that are usually neglected. The full Coriolis force in 3-dimensions is:
\(\ \begin{align} \frac{F_{x\ C F}}{m}=f_{c} \cdot V-2 \Omega \cdot \cos (\phi) \cdot W\tag{10.17c}\end{align}\)
[small because often W<<V]
\(\ \begin{align} \frac{F_{y\ C F}}{m}=-f_{c} \cdot U\tag{10.17d}\end{align}\)
\(\ \begin{align} \frac{F_{z\ C F}}{m}=2 \Omega \cdot \cos (\phi) \cdot U\tag{10.17e}\end{align}\)
[small relative to other vertical forces]
Gaspar Gustave Coriolis explained a compound centrifugal force on a rotating non-spherical planet such as Earth (Anders Persson: 1998, 2006, 2014).
Basics
On the rotating Earth an imbalance can occur between gravitational force and centrifugal force.
For an object of mass m moving at tangential speed Mtan along a curved path having radius of curvature R, centrifugal force was shown earlier in this chapter to be FCN/m = (Mtan)2/R. In Fig 10.a the object is represented by the black dot, and the center of rotation is indicated by the X.
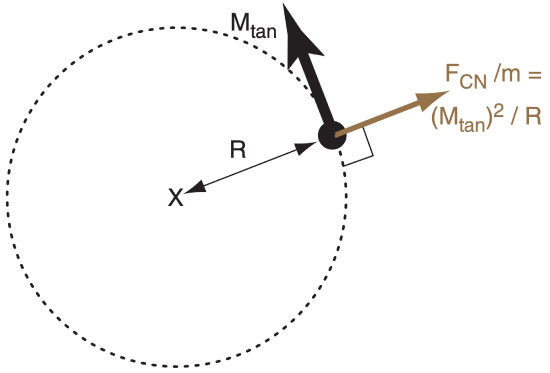
The Earth was mostly molten early in its formation. Although gravity tends to make the Earth spherical, centrifugal force associated with Earth’s rotation caused the Earth to bulge slightly at the equator. Thus, Earth’s shape is an ellipsoid (Fig. 10.b).
The combination of gravity FG and centrifugal force FCN causes a net force that we feel as effective gravity FEG. Objects fall in the direction of effective gravity, and it is how we define the local vertical (V) direction. Perpendicular to vertical is the local “horizontal” (H) direction, along the ellipsoidal surface. An object initially at rest on this surface feels no net horizontal force. [Note: Except at the poles and equator, FG does not point exactly to Earth’s center, due to gravitational pull of the equatorial bulge.]

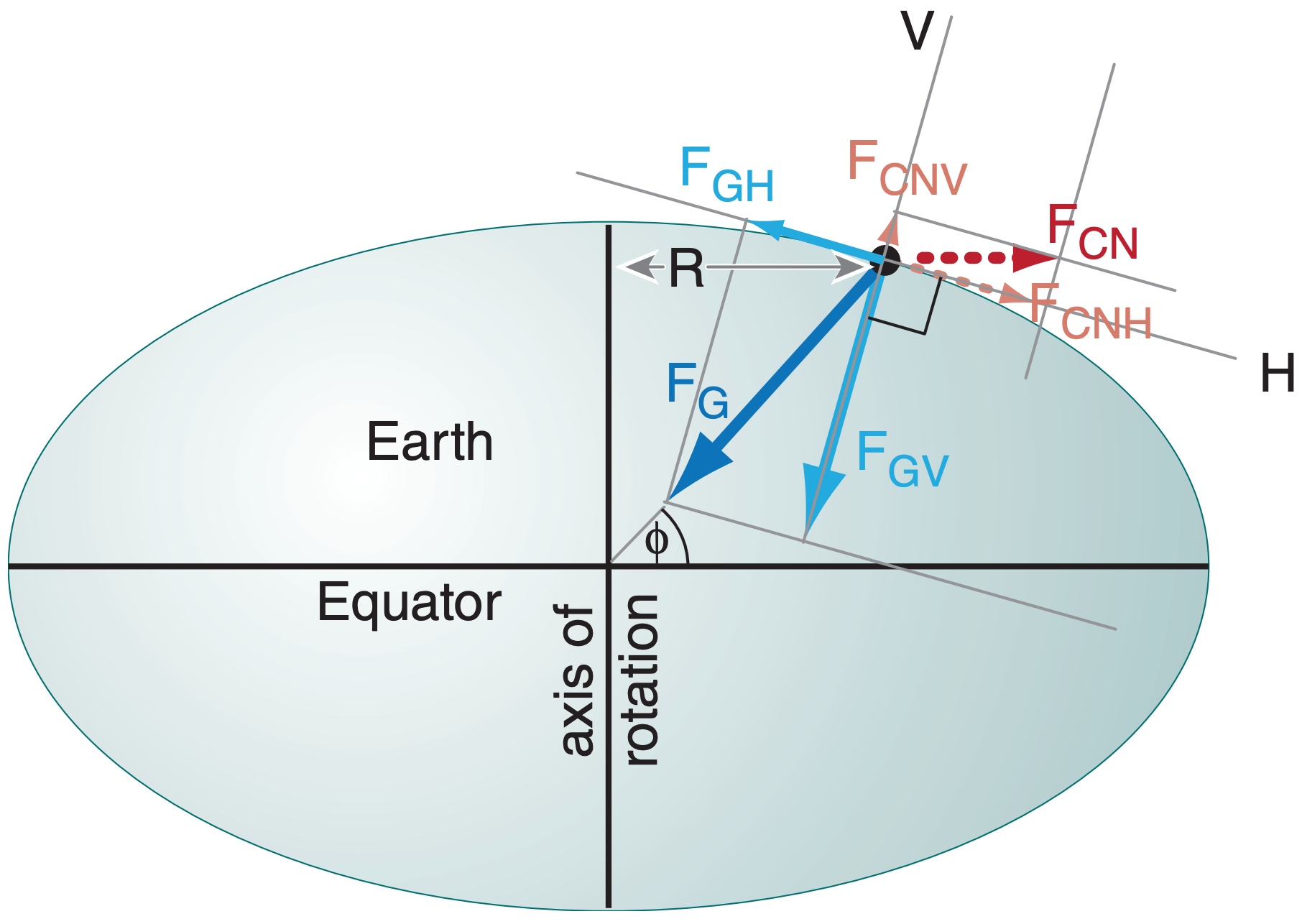
Split the vectors of true gravity into local vertical FGV and horizontal FGH components. Do the same for the centrifugal force (FCNV , FCNH) of Earth’s rotation (Fig. 10.c). Total centrifugal force FCN is parallel to the equator (EQ). Thus, for an object at latitude ϕ , you can use trig to show FCNH ≈ FCN·sin(ϕ).
Objects at Rest with respect to Earth’s Surface
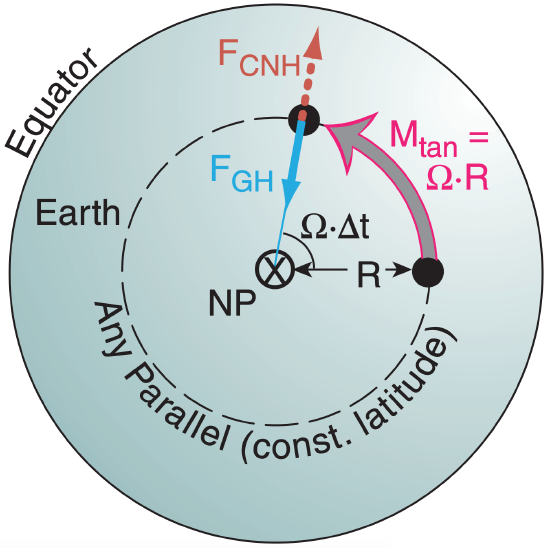
Looking down towards the north pole (NP), the Earth turns counterclockwise with angular velocity Ω = 360°/(sidereal day) (Fig. 10.d). Over a time interval ∆t, the amount of rotation is Ω·∆t. Any object (black dot) at rest on the Earth’s surface moves with the Earth at tangential speed Mtan = Ω·R (grey arrow), where R = Ro·cos(ϕ) is the distance from the axis of rotation. Ro = 6371 km is average Earth radius.
But because the object is at rest, its horizontal component of centrifugal force FCNH associated with movement following the curved latitude (called a parallel) is the same as that for the Earth, as plotted in Fig. 10.c above. But this horizontal force is balanced by the horizontal component of gravity FGH, so the object feels no net horizontal force.
Objects Moving East or West relative to Earth
Suppose an object moves with velocity M due east relative to the Earth. This velocity (thin white arrow in Fig. 10.e) is relative to Earth’s velocity, giving the object a faster total velocity (grey arrow), causing greater centrifugal force and greater FCNH. But FGH is constant.
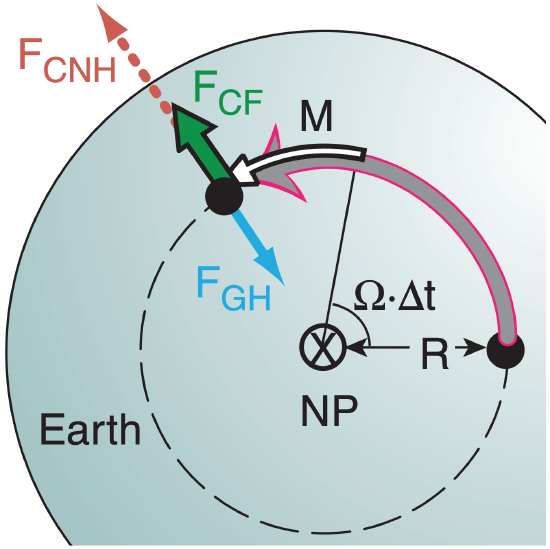
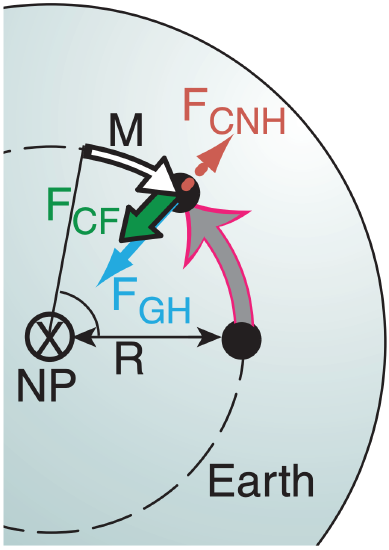
Horizontal force FCNH does NOT balance FGH. The thick green arrow (Fig. 10.e) shows that the force difference FCF is to the right relative to the object’s motion M. FCF is called Coriolis force.
The opposite imbalance of FCNH and FGH occurs for a westward-moving object (thin white arrow), because the object has slower net tangential velocity (grey arrow in Fig. 10.f). This imbalance, Coriolis force FCF (green arrow), is also to the right of the relative motion M.
Northward-moving Objects
When an object moves northward at relative speed M (thin white arrow in Fig. 10.g) while the Earth is rotating, the path traveled by the object (thick grey line) has a small radius of curvature about point X that is displaced from the North Pole. The smaller radius R causes larger centrifugal force FCNH pointing outward from X.
Component FCNH-ns of centrifugal force balances the unchanged horizontal gravitational force FGH. But there remains an unbalanced east-west component of centrifugal force FCNH-ew which is defined as Coriolis force FCF (green arrow). Again, it is to the right of the relative motion vector M of the object.

Objects moving south have a Coriolis force to the right due to the larger radius of curvature. Regardless of the direction of motion in the Northern Hemisphere, Coriolis force acts 90° to the right of the object’s motion relative to the Earth. When viewing the Southern Hemisphere from below the south pole, the Earth rotates clockwise, causing a Coriolis force that is 90° to the left of the relative motion vector.
Coriolis-force Magnitude Derivation
From Figs. 10.c & d, see that an object at rest (subscript R) has
\(\ \begin{align} F_{G H}=F_{C N H} \equiv F_{C N H R}\tag{C1}\end{align}\)
and
\(\ \begin{align} M_{\text {tan rest}}=\Omega \cdot R\tag{C2}\end{align}\)
From Fig. 10.e, Coriolis force for an eastward-moving object is defined as
FCF ≡ FCNH – FGH
Apply eq. (C1) to get
FCF = FCNH – FCNHR
or
FCF = sin(ϕ) · [FCN – FCNR] (from Fig. 10.c)
Divide by mass m, and plug in the definition for centrifugal force as velocity squared divided by radius:
FCF / m = sin(ϕ) · [ (Mtan)2/R – (Mtan rest)2/R ]
Use Mtan = Mtan rest + M, along with eq. (C2):
FCF / m = sin(ϕ) · [ (Ω·R+M)2/R – (Ω·R)2/R ]
FCF / m = sin(ϕ) · [(2·Ω·M) + (M2/R)]
The first term is usually much larger than the last, allowing the following approximation for Coriolis force per mass:
\(\ \begin{align} F_{C F} / m \approx 2 \cdot \Omega \cdot \sin (\phi) \cdot M\tag{10.18}\end{align}\)
Define a Coriolis parameter as fc ≡ 2·Ω·sin(ϕ) . Thus,
\(F_{C F} / m \approx f_{\mathrm{c}} \cdot M\)
In vector form, centrifugal force/mass for an object at rest on Earth is –Ω × (Ω × r), and Coriolis force/mass is –2Ω × V , where vector Ω points along the Earth’s axis toward the north pole, r points from the Earth’s center to the object, V is the object’s velocity relative to Earth, and × is the vector cross product.
10.3.5. Turbulent-Drag Force
Surface elements such as pebbles, blades of grass, crops, trees, and buildings partially block the wind, and disturb the air that flows around them. The combined effect of these elements over an area of ground is to cause resistance to air flow, thereby slowing the wind. This resistance is called drag.
At the bottom of the troposphere is a layer of air roughly 0.3 to 3 km thick called the atmospheric boundary layer (ABL). The ABL is named because it is at the bottom boundary of the atmosphere. Turbulence in the ABL mixes the very-slow near-surface air with the faster air in the ABL, reducing the wind speed M throughout the entire ABL (Fig. 10.7).
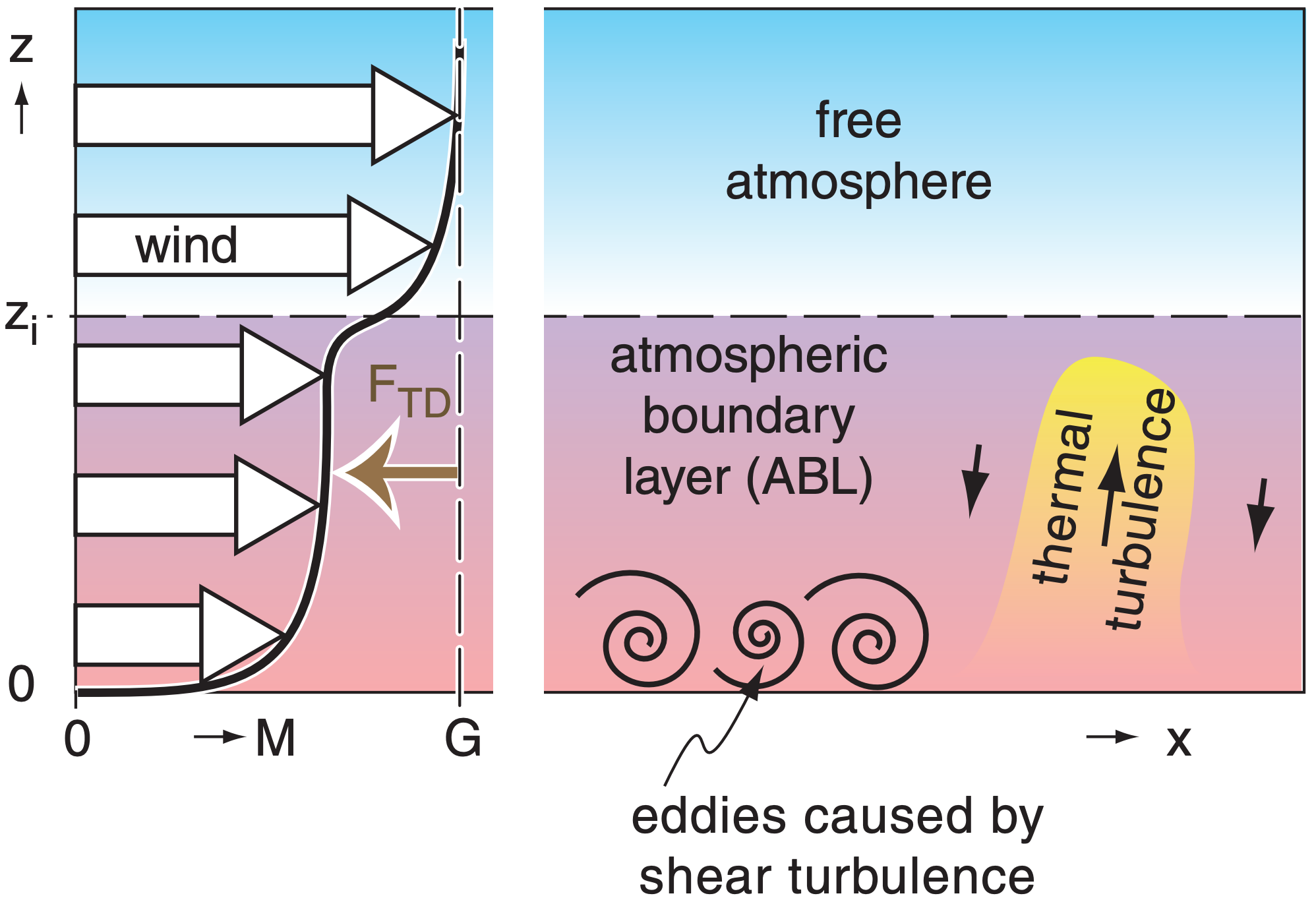
The net result is a drag force that is normally only felt by air in the ABL. For ABL depth zi the drag is:
\(\ \begin{align} \frac{F_{x\ T D}}{m}=-w_{T} \cdot \frac{U}{z_{i}}\tag{10.19a}\end{align}\)
\(\ \begin{align} \frac{F_{y\ T D}}{m}=-w_{T} \cdot \frac{V}{z_{i}}\tag{10.19b}\end{align}\)
where wT is called a turbulent transport velocity. The total magnitude of turbulent drag force is
\(\ \begin{align} \left|\frac{F_{T D}}{m}\right|=w_{T} \cdot \frac{M}{z_{i}}\tag{10.20}\end{align}\)
and is always opposite to the wind direction.
For statically unstable ABLs with light winds, where a warm underlying surface causes thermals of warm buoyant air to rise (Fig. 10.7), this convective turbulence transports drag information upward at rate:
\(\ \begin{align} w_{T}=b_{D} \cdot w_{B}\tag{10.22}\end{align}\)
where dimensionless factor bD = 1.83x10–3. The buoyancy velocity scale, wB, is of order 10 to 50 m s–1, as is explained in the Heat Budget chapter
For statically neutral conditions where strong winds M and wind shears (changes of wind direction and/or speed with height) create eddies and mechanical turbulence near the ground (Fig. 10.7), the transport velocity is
\(\ \begin{align} w_{T}=C_{D} \cdot M\tag{10.21}\end{align}\)
where the drag coefficient CD is small (2x10–3 dimensionless) over smooth surfaces and is larger (2x10–2) over rougher surfaces such as forests.
In fair weather, turbulent-drag force is felt only in the ABL. However, thunderstorm turbulence can mix slow near-surface air throughout the troposphere. Fast winds over mountains can create mountain-wave drag felt in the whole atmosphere (see the Regional Winds chapter).
Sample Application
What is the drag force per unit mass opposing a U = 15 m s–1 wind (with V = 0) for a: (a) statically neutral ABL over a rough forest; & (b) statically unstable ABL having convection with wB = 50 m s–1, given zi = 1.5 km.
Find the Answer
Given: U = M = 15 m s–1, zi = 1500 m, CD = 2x10–2, wB = 50 m s–1.
Find: Fx TD/m = ? m·s–2.
(a) Plugging eq. (10.21) into eq. (10.19a) gives:
\(\frac{F_{x\ T D}}{m}=-C_{D} \cdot M \cdot \frac{U}{z_{i}}=-(0.02) \cdot \frac{(15 \mathrm{m} / \mathrm{s})^{2}}{1500 \mathrm{m}}\)
= –3x10–3 m·s–2.
(b) Plugging eq. (10.22) into eq. (10.19a) gives:
\(\frac{F_{x\ T D}}{m}=-b_{D} \cdot w_{B} \cdot \frac{U}{z_{i}}\)
\(=-(0.00183) \cdot(50 \mathrm{m} / \mathrm{s}) \cdot \frac{(15 \mathrm{m} / \mathrm{s})}{1500 \mathrm{m}}\)
= –9.15x10–4 m·s–2.
Check: Physics and units are reasonable.
Exposition: Because the wind is positive (blowing toward the east) it requires that the drag be negative (pushing toward the west). Shear (mechanical) turbulence and convective (thermal/buoyant) turbulence can both cause drag by diluting the faster winds higher in the ABL with slower near-surface winds.
| Table 10-3. Summary of forces. | |||||
| Item | Name of Force | Direction | Magnitude (N kg–1) | Horiz. (H) or Vert. (V) | Remarks (“item” is in column 1; H & V in col. 5) |
|---|---|---|---|---|---|
| 1 | gravity | down | \(\left|\frac{F_{G}}{m}\right|=|g|=9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\) | V | hydrostatic equilibrium when items 1 & 2V balance |
| 2 | pressure gradient | from high to low pressure | \(\left|\frac{F_{P G}}{m}\right|=\left|g \cdot \frac{\Delta z}{\Delta d}\right|\) | V & H | the only force that can drive horizontal winds |
| 3 | Coriolis (compound) | 90° to right (left) of wind in Northern (Southern) Hemisphere | \(\left|\frac{F_{C F}}{m}\right|=2 \cdot \Omega \cdot|\sin (\phi) \cdot M|\) | H* | geostrophic wind when 2H and 3 balance (explained later in horiz. wind section) |
| 4 | turbulent drag | opposite to wind | \(\left|\frac{F_{T D}}{m}\right|=w_{T} \cdot \frac{M}{z_{i}}\) | H* | atm. boundary-layer wind when 2H, 3 and 4 balance (explained in horiz. wind section) |
| 5 | centrifugal (apparent) | away from center of curvature | \(\left|\frac{F_{C N}}{m}\right|=\frac{M^{2}}{R}\) | H* | centripetal = opposite of centrifugal. Gradient wind when 2H, 3 and 5 balance |
| 6 | advection (apparent) | (any) | \(\left|\frac{F_{A D}}{m}\right|=|-M \cdot \frac{\Delta U}{\Delta d}-\cdots|\) | V & H | neither creates nor destroys momentum; just moves it |
*Horizontal is the direction we will focus on. However, Coriolis force has a small vertical component for zonal winds. Turbulent drag can exist in the vertical for rising or sinking air, but has completely different form than the boundary-layer drag given above. Centrifugal force can exist in the vertical for vortices with horizontal axes. Note: units N kg–1 = m·s–2.


