7.6: Collision and Collection
- Page ID
- 9573
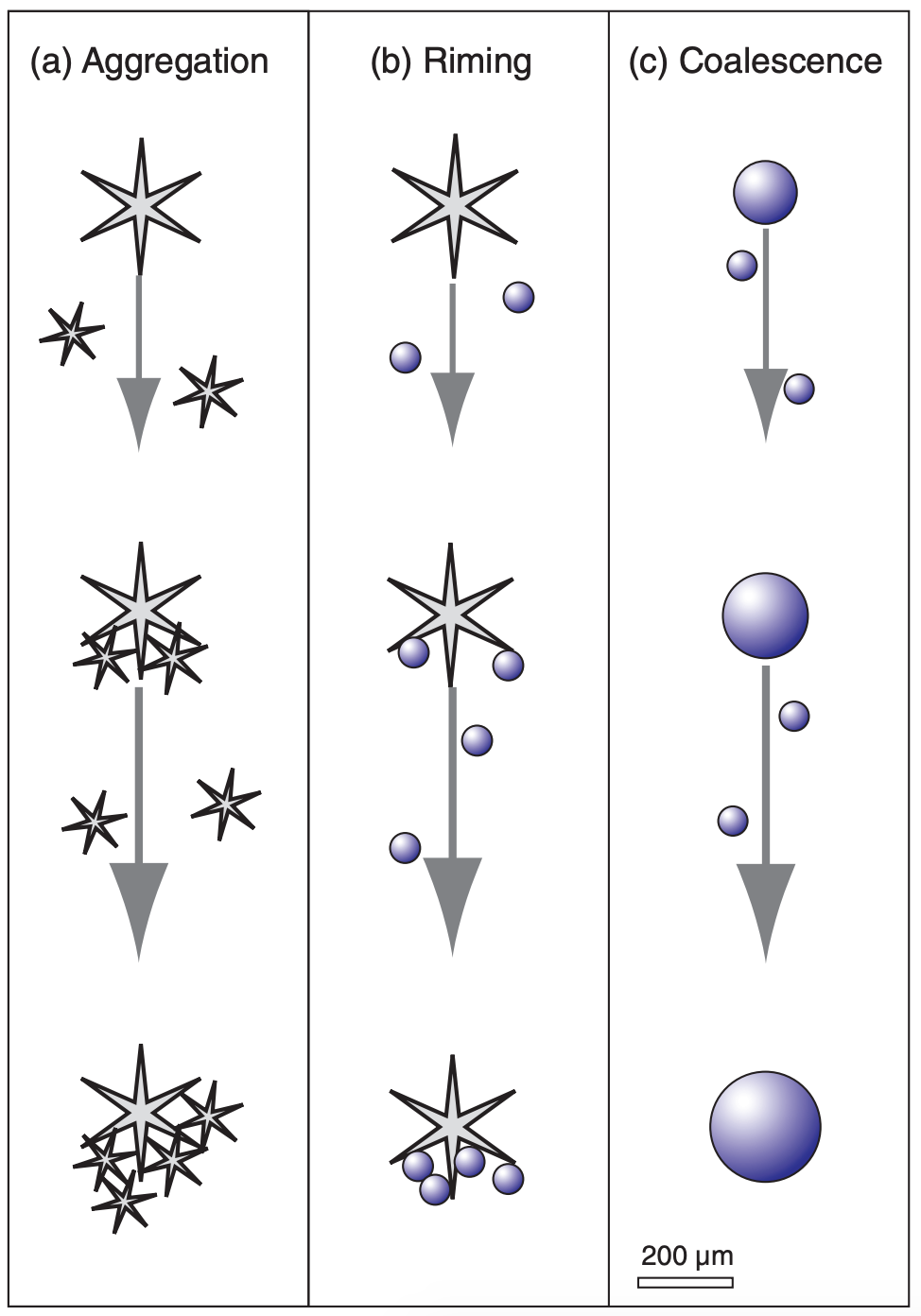
Larger hydrometeors (ones with a greater mass/ drag ratio) fall the fastest. As a result, different hydrometeors move at different speeds, allowing some to collide (hit each other). Not all collisions result in the merging of two hydrometeors. Those particles that do merge form a particle that is even heavier, falls faster, and collides with even more particles (Fig. 7.17). Hence, this positive feedback can cause hydrometeors to rapidly grow large enough to precipitate.
7.6.1. Terminal Velocity of Hydrometeors
Everything including cloud and rain drops is pulled by gravity. The equilibrium velocity resulting when gravity balances frictional drag is called the terminal velocity.
7.6.1.1. Cloud Droplets
For particles of radius R < 40 µm, which includes most cloud droplets and aerosols, Stokes Drag Law gives the terminal velocity wT as
\(\ \begin{align}w_{T} \approx-k_{1} \cdot R^{2}\tag{7.29}\end{align}\)
where k1 = 1.19x108 m–1·s–1 . The negative sign on indicates the droplets are falling.
When drops fall at their terminal velocity, the gravitational pull on the drops is transmitted by frictional drag to the air. In other words, the weight of the air includes the weight of the drops within it. Hence, droplet-laden air is heavier than cloud-free air, and behaves as if it were colder (see virtual temperature, eq. 1.22). Falling rain also tends to drag air with it.
Typical terminal velocities of these smallest droplets and aerosols are mm s–1 to cm s–1 relative to the air. However, the rising air in clouds often has updraft velocities (cm s–1 to m s–1) that are greater than the terminal velocity of the particles. The net result is that cloud droplets and aerosols are carried upward inside the cloud.
Sample Application
What updraft wind is needed to keep a typical cloud droplet (R = 10 µm) from falling?
Find the Answer
Given: R = 10 µm
Find: wT = ? m s–1, and use: wup = – wT
Use eq. (7.29):
wT = (–1.19x108 m–1 s–1)·(10x10–6 m)2 = = –0.012 m s–1 = –1.2 cm s–1
wup = 1.2 cm s–1
Check: Units OK. Physics OK.
Exposition: The required updraft velocity is positive 1.2 cm s–1, which is a very gentle movement of air. Recalling that most clouds form by adiabatic cooling within updrafts of air, these updrafts also keep cloud droplets aloft.
7.6.1.2. Rain Drops
Rain drops are sufficiently large and fall fast enough that Stokes drag law is not appropriate. If raindrops were perfect spheres, then
\(\ \begin{align} w_{T} \approx-k_{2} \cdot\left(\frac{\rho_{o}}{\rho_{a i r}} \cdot R\right)^{1 / 2}\tag{7.30}\end{align}\)
where k2 = 220 m1/2·s–1, ρo = 1.225 kg·m–3 is air density at sea level, and ρair is air density at the drop altitude. Again, the negative sign in the equation means a downward velocity.
However, the larger raindrops become flattened as they fall due to the drag (see polarimetric radar section of the Satellites & Radar chapter). They do not have a tear-drop shape. This flattening increases air drag even further, and reduces their terminal velocity from that of a sphere. Fig. 7.18 shows raindrop terminal velocities. For the smallest drops, the curve has a slope of 2, corresponding to Stokes law. For intermediate sizes R = 500 to 1000 µm, the slope is 0.5, which corresponds to eq. (7.30). At the larger sizes about R = 2.5 mm, the terminal velocity curve has near zero slope as the droplet becomes so deformed that it begins to look like a parachute. Drops larger than about 2.5 mm radius tend to break up. The largest raindrops rarely exceed 4 mm radius.

Let R be the equivalent radius of a sphere having the same volume as the deformed drop. An empirical curve for terminal velocity (relative to air) over range 20 ≤ R ≤ 2500 µm is:
\(\ \begin{align} w_{T}=-c \cdot\left[w_{o}-w_{1} \cdot \exp \left(\frac{R_{o}-R}{R_{1}}\right)\right]\tag{7.31}\end{align}\)
where wo = 12 m s–1, w1 = 1 m s–1, Ro = 2500 µm, and R1 = 1000 µm. This curve gives a maximum terminal velocity of 11 m s–1 for the largest drops. The density correction factor is c = (ρ70kPa/ρair) 1/2 ≈ (70 kPa/P) 1/2, where P is ambient pressure. Rain falls faster where the air is thinner (less dense).
Sample Application
Find the terminal velocity of a droplet of equivalent radius 1500 µm, at P = 70 kPa.
Find the Answer
Given: R = 1500 µm, c = 1 at P = 70 kPa.
Find: wT = ? m s–1.
Use eq. (7.31):
wT = –1·[(12m s–1) – (1m s–1)· exp{(2500µm–1500µm)/(1000µm)}] = –9.3 m s–1
Check: Units OK. Physics OK. Agrees with Fig. 7.18. Negative sign means falling downward.
Exposition: This wT ≈ 34 km h–1. Updrafts in thunderstorms are fast, and keep these large drops aloft.
7.6.1.3. Hailstones
The terminal velocity wT of a hailstone relative to the air is approximated by:
\(\ \begin{align} w_{T}=-\left[\frac{8}{3} \frac{|g|}{C_{D}} \frac{\rho_{i}}{\rho_{a i r}} R\right]^{1 / 2}\tag{7.32}\end{align}\)
where |g| = 9.8 m s–2 is gravitational acceleration magnitude, CD ≈ 0.55 (dimensionless) is a drag coefficient of the hailstone through air, ρi ≈ 900 kg m–3 is the density of the hailstone, ρair is air density, and R is hailstone radius. The negative sign means the hailstone falls downward.
The drag coefficient varies between 0.4 and 0.8, because hailstones have different shapes, surface roughnesses, and tumblings. The hailstone ice density can be less than the density of pure ice, because of varying amounts of imbedded air bubbles. Air density decreases with increasing altitude (see Chapter 1); hailstones fall faster in thinner air. For non-spherical hailstones, R is taken as the equivalent radius of a sphere that has the same volume as the actual hailstone.
Large hailstones form only in thunderstorms with strong updrafts. Thus, the hailstone terminal velocity relative to the ground is the sum of the air updraft speed (a positive number) and the hailstone terminal velocity relative to the air (a negative number).
Sample Application
Plot the terminal velocity of hailstones vs. equivalent diameter (0.01 to 0.1 m) at 5 km altitude.
Find the Answer
Given: z = 5 km
Find: wT (m s–1) vs. D (m), where D = 2·R .
Assume: std. atmosphere. Thus ρair = 0.7361 kg m–3 at z = 5 km, from Chapter 1.
Assume: CD = 0.55, and ρi = 900 kg m–3 , calm air.
Use a spreadsheet to solve eq. (7.32).
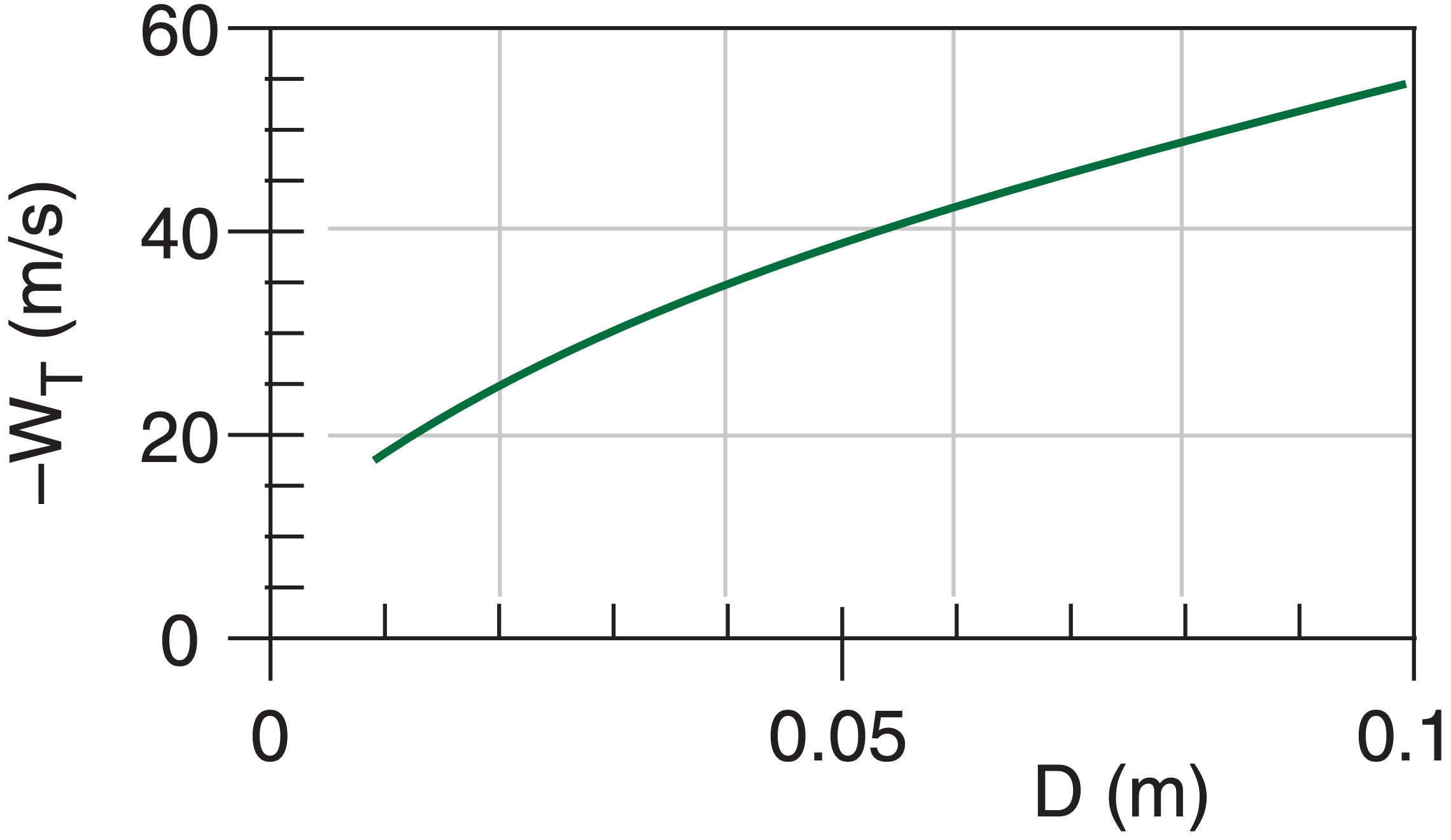
Check: Magnitudes agree with plot in the Thunderstorm chapters. Sign is negative (implying downward fall).
Exposition: Massive hailstones falling at these fast velocities can kill people, strip foliage and small branches off trees, destroy crops, and kill animals.
7.6.2. Collection & Aggregation Processes
7.6.2.1. Warm-cloud Process
The merging of two liquid droplets (Fig. 7.17c) is called coalescence. This is the only process for making precipitation-size hydrometeors that can happen in warm clouds (clouds warmer than 0°C), and is thus called the warm-cloud process.
When droplets of different size approach each other, they do not always merge. One reason is that the smaller droplet partly follows the air as it flows around the larger droplet, and thus may not collide with the larger drop (Fig. 7.19). This is quantified by a collision efficiency (E), which is small (0.02 < E < 0.1) when the smaller droplet is very small ( 2 < R < 5 µm). But if both droplets are relatively large (such as when the smaller droplet has R > 10 µm, and the larger droplet has R > 30 µm), then efficiencies can be 0.5 ≤ E ≤ 1.
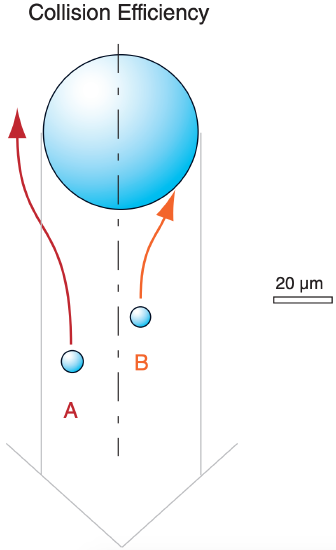
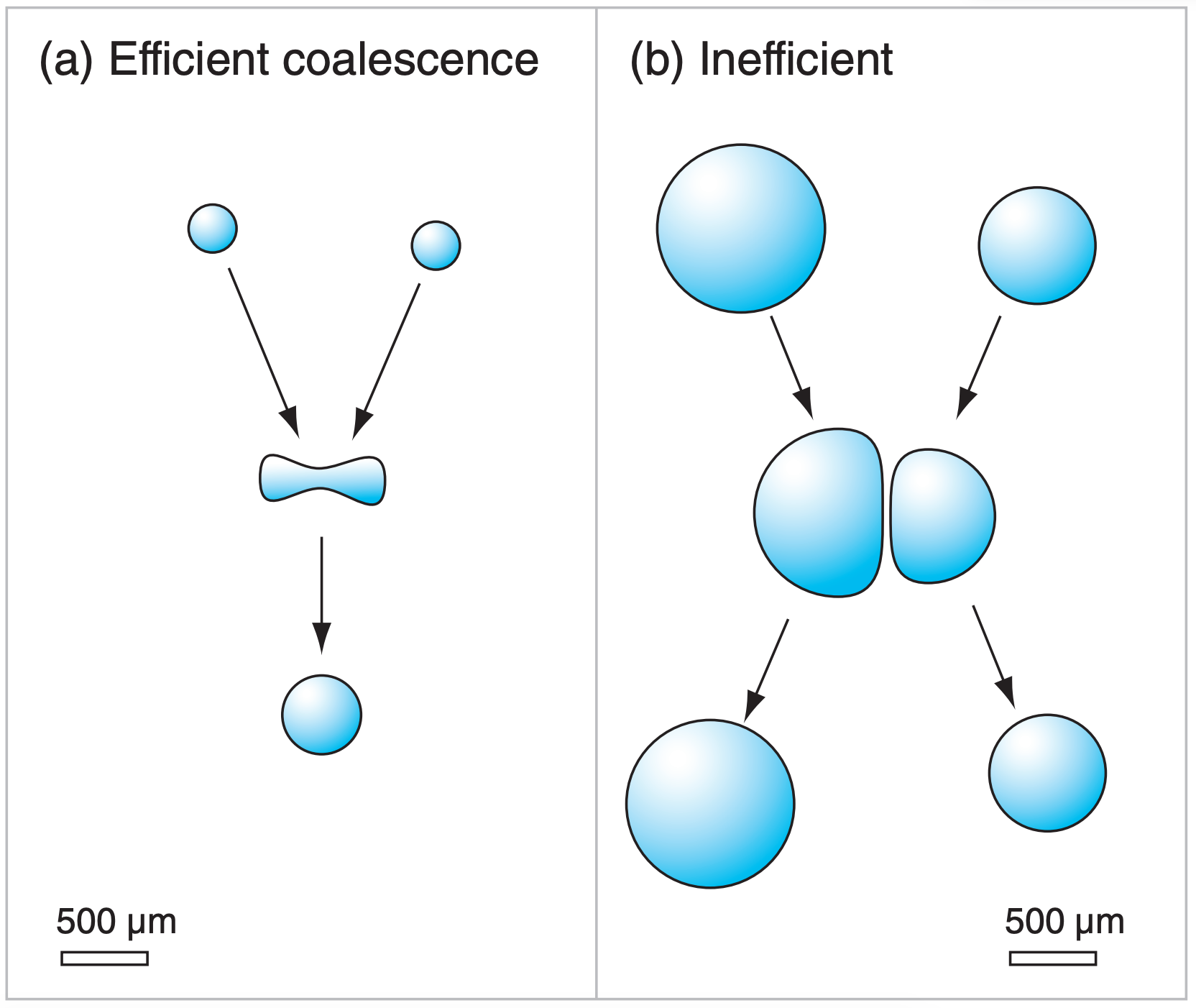
Even if two droplets collide, they might not merge because a thin layer of air can be trapped between the two droplets (Fig. 7.20b). For this situation, the two droplets bounce off of each other and do not coalesce. The coalescence efficiency (E’) is very small (0.1 ≤ E’ ≤ 0.3) when both drops are large (300 ≤ R ≤ 500 µm). The efficiency is greater (E’ > 0.8) when both droplets are small (R < 150 µm, as in Fig. 7.20a).
The product of both efficiencies is the collection efficiency: Ec = E · E’ . The maximum efficiency possible is 1.0, but usually efficiencies are smaller.
7.6.2.2. Cold-cloud Processes
When ice particles collide and stick to other ice particles (Fig. 7.17a), the process is called aggregation. Such aggregation is aided if the colliding particles are dendrites, for which the snowflake arms can interlock. Also, if the ice particles are warmer than –5°C, then the ice surface becomes sticky, allowing multiple ice crystals to aggregate into soft little irregular clumps of snow.
The growth of ice particles by collection and instant freezing of supercooled liquid droplets (Fig. 7.17b) in mixed-phase clouds is called accretion or riming. Hydrometeors that become so heavily rimed as to completely cover and mask the original habit are called graupel. Graupel has the consistency of a sugar cube (i.e., many separate solid grains stuck together), but often in the shape of a cone or a sphere. For an aggregate to be called graupel, it’s diameter must be no larger than 5 mm.
If the collected water does not freeze instantly upon contacting the ice particle, but instead flows around it before freezing, then hail can form. Graupel contains a lot of air trapped between the frozen droplets on the graupel, and thus is often softer and less dense than hail. See the Thunderstorm chapters for more information about hail.
7.6.3. Precipitation Formation
7.6.3.1. Warm Clouds
How do terminal velocity and collection efficiency relate to the formation of large, precipitation-size particles in warm clouds? Recall that: (1) the atmosphere has an excessively large number of CCN; (2) this causes the available condensate in a rising cooling air parcel to be partitioned into a large number of small droplets (droplets too small to rain out); (3) droplets tend to become monodisperse (nearly the same size) due to diffusion; (4) droplets of the same size have the same terminal velocity, and thus would be unlikely to collide with each other as they are kept aloft in the updraft; and (5) with no collisions we would not expect larger precipitation drops to form in warm clouds.
Yet warm-cloud rain happens quite nicely in the real atmosphere, especially in the tropics. Why?
Ancient Greeks defined “meteors” as anything in the sky. They were particularly concerned about missiles the gods might toss down, such as bits of rock, ice, or lightning bolts.
Only much later did scientists discriminate between missiles from space (bits of rock called meteoroids) and missiles from the atmosphere (bits of just about anything else from the sky). But by then “meteorology” was firmly entrenched as the name for atmospheric science.
According to the Glossary of Meteorology, meteorologists study the following meteors:
- hydrometeors – wet: clouds, rain, snow, fog, dew, frost, etc.
- lithometeors – dry: dust, sand, smoke, haze
- igneous meteors – lightning, corona
- electrometeors – lightning (again), thunder
- luminous meteors – rainbows, halos, etc.
Except for “hydrometeors”, these terms are seldom used any more.
Five factors can help make warm-cloud rain:
- First, by random chance a small number of collisions do occur, which starts to broaden the spectrum of drop sizes. This broadens the range of terminal velocities to allow more collisions, which accelerates via positive feedback (with help from breakup of larger drops).
- Second, not all CCN are the same size — some are called giant CCN (particles > 3 µm radius, with a wettable surface) and can create a small number of larger cloud droplets that fall relative to (and collide with) the other cloud droplets.
- Third, turbulence can entrain outside clear air into the top and sides of a cloud, causing some droplets to partly evaporate, thereby broadening the spectrum of droplet sizes, again allowing collisions.
- Fourth, IR radiation from individual drops near cloud top and sides can cool the drops slightly below the ambient air temperature, allowing greater condensation growth of those drops relative to interior drops.
- Fifth, electrical charge build-up in cumuliform clouds (see the Thunderstorm chapters) can draw droplets together of different charge, and can cause sparks between nearby droplets to allow them to coalesce more efficiently.
7.6.3.2. Cold Clouds
In cold clouds (T < 0°C), the smaller number of ice nuclei in the atmosphere allows the available condensate to deposit onto a small number of larger ice particles. Even in mixed-phase clouds, the WBF process can remove water molecules from the large number of droplets and deposit them onto a small number of ice crystals. Thus, the ice crystals are larger, and can fall as precipitation. Also, the crystals often have a wide range of sizes and shapes so they can collide and aggregate easily, which also creates large-enough particles to fall as precipitation.
Cumuliform clouds including thunderstorms can be deep enough to have their bases in warm air and their tops in cold air (Fig. 7.21). Thus, ice particles can grow to large size (order of 1-5 mm) via the WBF process, aggregation, and riming in the cold part of the cloud, and then melt into large raindrops as they pass through warmer air closer to the ground. Most rain from mid-latitude thunderstorms forms this way. See the Thunderstorm chapters for more information about heavy rain.
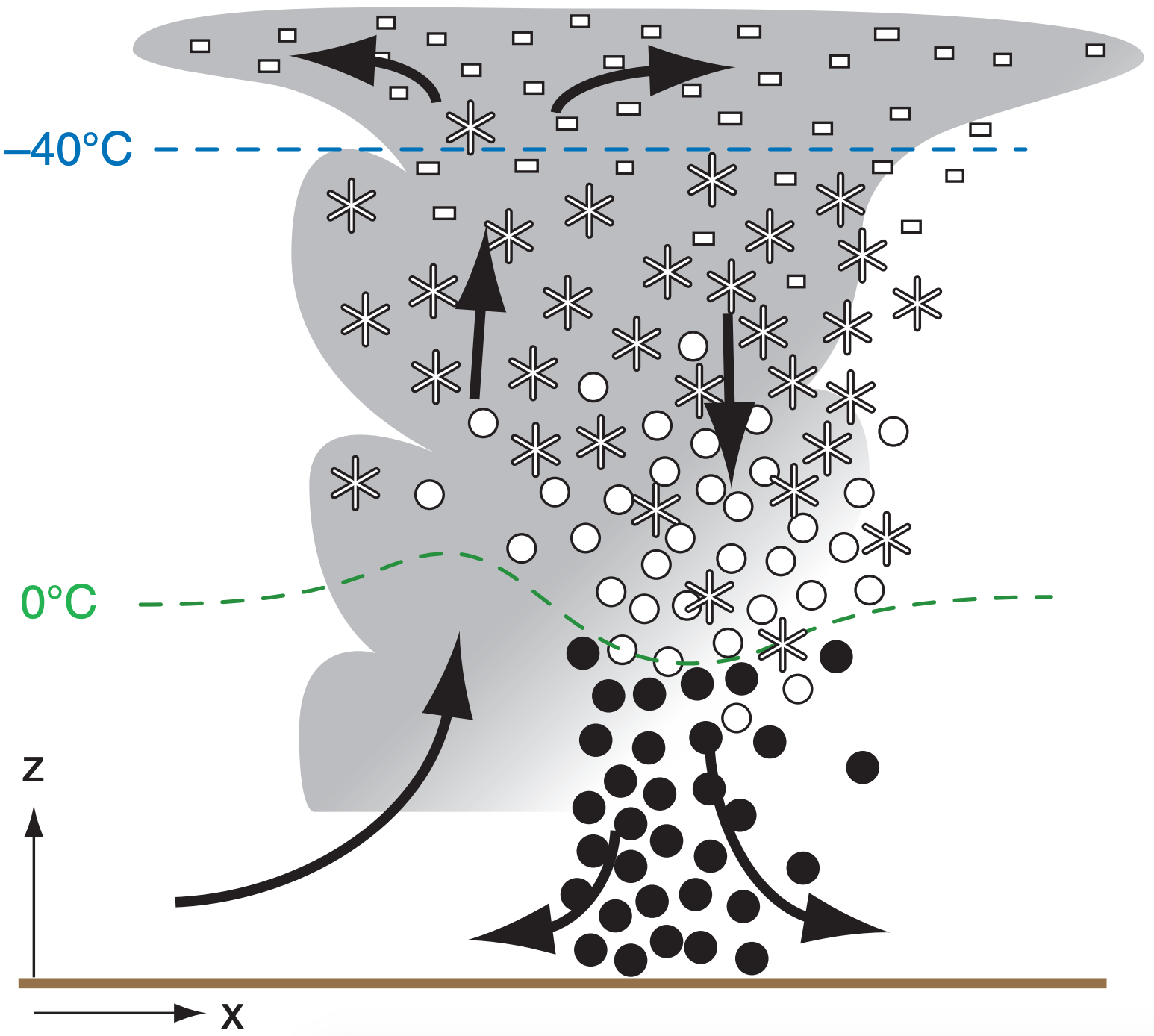
Also, on those rare occasions when thunderstorms can be triggered in late Fall or early Spring, boundary-layer temperatures can be cold enough to allow snow from thunderstorms to reach the ground as large snow clusters (snow balls) without totally melting, accompanied by lightning and thunder from the storm. This is sometimes nicknamed thundersnow.
Regardless of whether clouds are warm or cold, a simple rule of precipitation is that thicker clouds can cause heavier precipitation rates with larger size drops. The main reason is that hydrometeors take a longer time to fall the greater distance through thicker clouds, giving them more time to grow.


