3.2: First Law of Thermodynamics
- Page ID
- 9541
3.2.1. Definition
Let ∆q (J kg–1) be the amount of thermal energy you add to a stationary mass m of air. Some of this energy warms the air (i.e., the internal energy increases). But as air warms, its volume expands by amount ∆V and pushes against the surrounding atmosphere (which to good approximation is pushing back with constant pressure P). Thus, a portion of the thermal energy input does not go into warming the air, but goes into macroscopic movement.
To illustrate, consider a column of air having base of area A and height d. Resting on top of this column is more air, the weight of which causes pressure P at the top of the column. Suppose the volume (V = A·d) expansion is all in the vertical, so that ∆V = A·∆d. For the column top to rise, it must counteract the downward pressure force from the air above; namely, the top of the column must push up with pressure P as it moves distance ∆d.
Recall that work W is force times distance (W = F·∆d). Also, pressure is force per unit area (P = F/A) Thus, the work done on the atmosphere by the expanding column is W = F·∆d = P·A·∆d = P·∆V.
The First Law of Thermodynamics says that energy is conserved, thus the thermal energy input must equal the sum of warming (a microscopic effect) and work done per unit mass (a macroscopic effect):
\(\ \begin{align}\Delta q=C_{v} \cdot \Delta T+P \cdot(\Delta V / m)\tag{3.2a}\end{align}\)
3.2.2. Apply to the Atmosphere
But P·(∆V/m) = ∆(P·V/m) – V·∆P/m (using the product rule of calculus). Also, P·V/m = P/ρ = ℜ·T from the ideal gas law, where ρ = m/V is air density and ℜ is the gas constant. Thus, ∆(P·V/m) = ∆(ℜ·T) = ℜ·∆T because ℜ is constant. Using this in eq. (3.2a) gives:
\(\ \begin{align}\Delta q=C_{v} \cdot \Delta T+\Re \cdot \Delta T-\Delta P / \rho\tag{3.2b}\end{align}\)
By definition for an ideal gas: Cv + ℜ ≡ Cp , where Cp is the specific heat of air at constant pressure. The INFO box on the next page gives:
\(\ \begin{align}C_{p}=C_{p h u m i d ~ a i r} \approx C_{p d} \cdot(1+1.84 \cdot r)\tag{3.3}\end{align}\)
where Cpd is the dry-air specific heat at constant pressure, and the water-vapor mixing ratio r has units (gwater vapor /gdry air). See the Water Vapor chapter for more details on humidity.
Appendix B lists some specific heats; e.g.:
Cpd air = 1004 J·kg–1·K–1 for dry air at const. pressure,
Cvd air = 717 J kg–1 K–1 for dry air at const. volume,
Cliq ≈ 4217.6 J·kg–1·K–1 for liquid water at 0°C,
Cice ≈ 2106 J·kg–1·K–1 for ice at 0°C,
Cpv = 1850 J·kg–1·K–1 for pure water vapor at 0°C.
You can combine the first two terms on the right of eq. (3.2b) to give a form of the First Law of Thermodynamics that is easier to use for the atmosphere:
\(\ \begin{align}\Delta q \quad=\quad C_{p} \cdot \Delta T \quad-\quad \Delta P / \rho\tag{3.2c}\end{align}\)
heat transferred enthalpy change
3.2.3. Enthalpy vs. Sensible Heat
From our derivation of eq. (3.2c) we saw that the first term on the right includes both the microscopic effect of a temperature change (internal energy or heat possessed) and the macroscopic effect of that same temperature change. Hence, we cannot call that term “heat possessed” — instead we need a new name.
To this end, define enthalpy as h = Cp·T with units J kg–1. The corresponding enthalpy change is:
\(\ \begin{align}\Delta h=C_{p} \cdot \Delta T\tag{3.4a}\end{align}\)
which is the first term on the right side of eq. (3.4). It is a characteristic possessed by the air.
By tradition, meteorologists often use the word sensible heat in place of the word enthalpy. This can be confusing because of the overloading of the word “heat”. Here is a table that might help you keep these definitions straight:
| Table 3-2. Heat terminology. | |||
| Quant. (J/kg) | Characteristic | Terminology | |
|---|---|---|---|
| Meteorology | Engineering | ||
| ∆q | transferred | heat transferred | heat |
| Cp·∆T | possessed | sensible heat | enthalpy |
With this in mind, the heat transferred per unit air mass can be annotated as follows:
\(\ \begin{align}\Delta q \quad=\quad C_{p} \cdot \Delta T \quad-\quad \Delta P / \rho\tag{3.2d}\end{align}\)
heat transferred sensible heat
This form is useful in meteorology. When rising air parcels experience a decrease in surrounding atmospheric pressure, the last term is non-zero.
The change of sensible-heat (∆QH) possessed by air mass mair changing its temperature by ∆T is thus:
\(\ \begin{align}\Delta Q_{H}=m_{a i r} \cdot C_{p} \cdot \Delta T\tag{3.4b}\end{align}\)
The specific heat at constant pressure Cp for air is the average of the specific heats for its constituents, weighted by their relative abundance:
\(\ \begin{align}m_{T} C_{p}=m_{d} \cdot C_{p d}+m_{v} \cdot C_{p v}\tag{3I.1}\end{align}\)
where mT = md + mv is the total mass of air (as a sum of mass of dry air md and water vapor mv), and Cpd and Cpv are the specific heats for dry air and water vapor, respectively.
Define a mixing ratio r of water vapor as r = mv / md. Typically, r is of order 0.01 g/g. Then eq. (3I.1) becomes:
\(\ \begin{align}C_{p}=(1-r) \cdot C_{p d} \cdot\left[1+r \cdot C_{p v} / C_{p d}\right]\tag{3I.2}\end{align}\)
Given: Cpd = 1004 J·kg–1·K–1 at 0°C for dry air, and Cpv = 1850 J·kg–1·K–1 for water vapor, eq. (3I.2) becomes
\(\ \begin{align}C_{p} \approx C_{p d} \cdot[1+1.84 \cdot r]\tag{3I.3}\end{align}\)
Even for dry air, the specific heat varies slightly with temperature, as shown in the figure below:
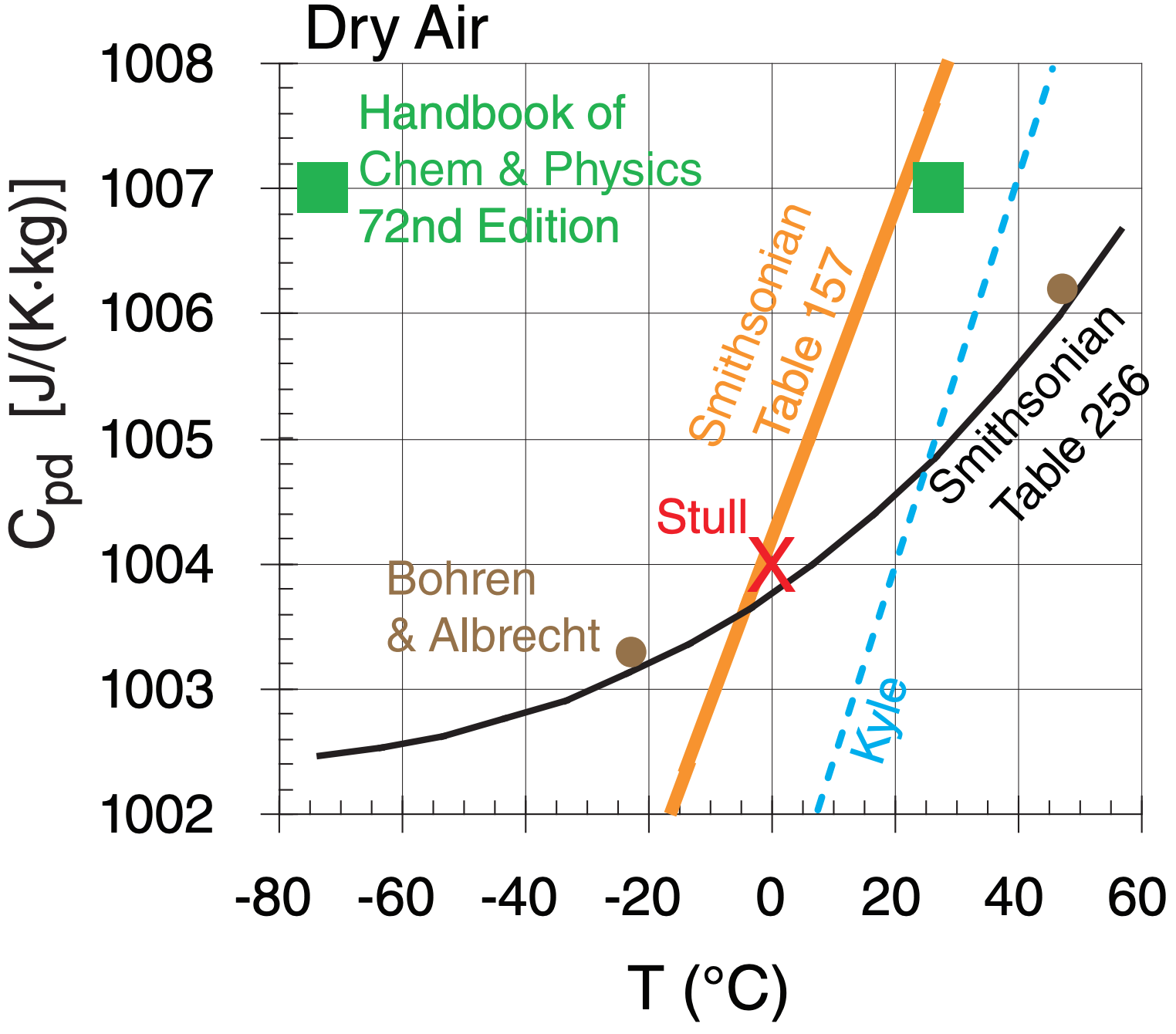 In this book, we will use Cpd = 1004 J·kg–1·K–1 , and will approximate it as being constant.
In this book, we will use Cpd = 1004 J·kg–1·K–1 , and will approximate it as being constant.Sample Application
What heat transfer is needed to cause 3 kg of dry air to cool by 10°C?
Find the Answer
Given: Cpd = 1004. J·kg–1·K–1, mair = 3 kg , ∆T = –10°C
Find: ∆QH = ? J
Apply eq. (3.4b):
∆QH = mair·Cpd·∆T = (3 kg)·(1004. J·kg–1·K–1)·(–10°C) = –30.12 kJ
Check: Physics & units are reasonable.
Exposition: On a hot day, this is the energy your air conditioner must extract from the air in your car
Cv — Specific Heat at Constant Volume
Consider a sealed box of fixed volume V filled with air, as sketched in Figure 3I.2a below. The number of air molecules (idealized by the little spheres) can’t change, so the air density ρ is constant. Suppose that initially, the air temperature To is cool, as represented by the short arrows denoting the movement of each molecule in box 3I.2a. When each molecule bounces off a wall of the container, it imparts a small force. The sum of forces from all molecules that bounce off a wall of area A results in an air pressure Po.
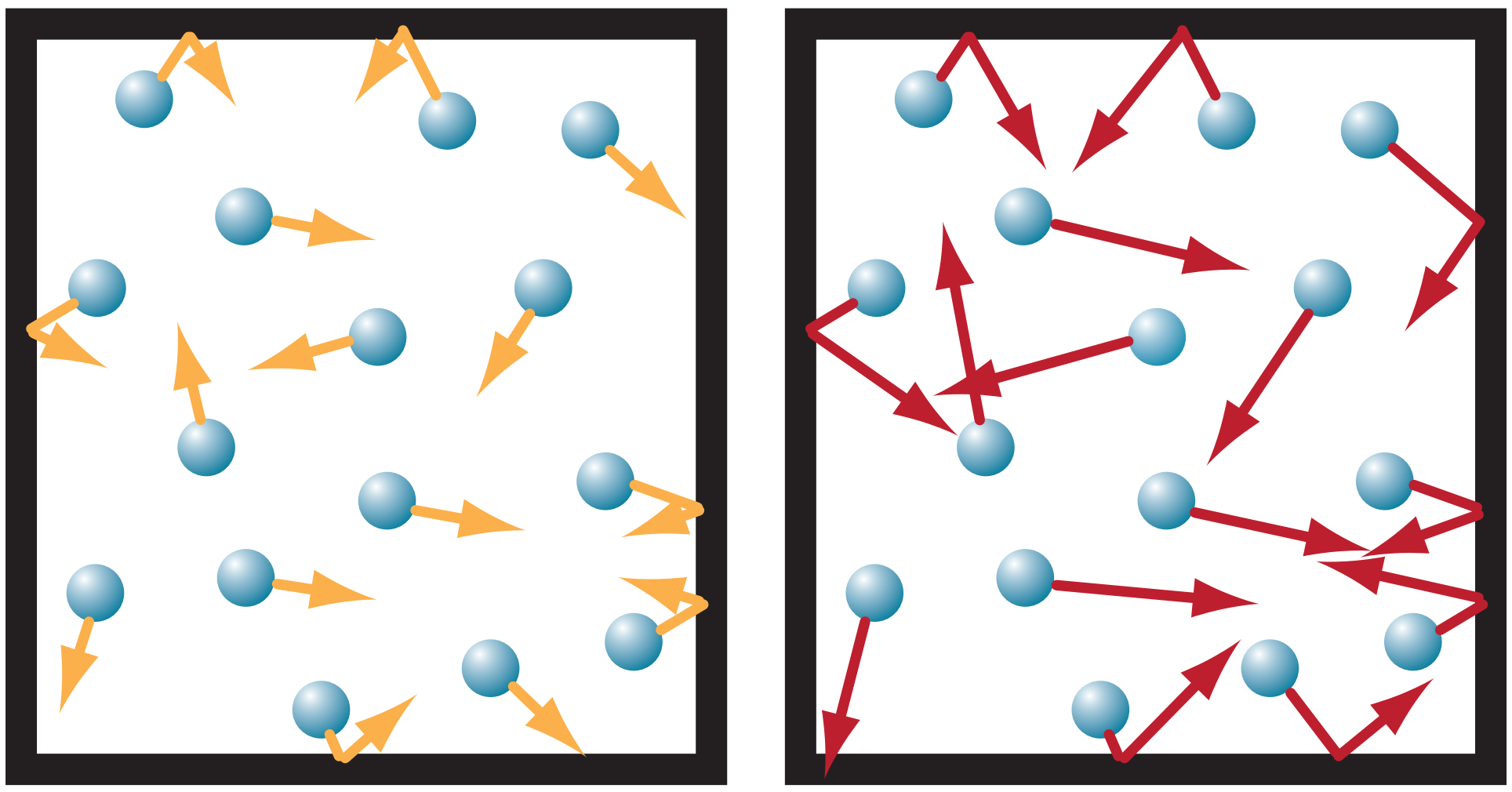
If you add ∆q thermal energy to air in the box, the temperature rises to T2 (represented by longer arrows in Figure 3I.2b).
Also, when each molecule bounces off a wall, it imparts a greater force because it is moving faster. Thus, the pressure P2 will be larger. This is expected from the ideal gas law under constant density, for which
\(\ \begin{align}P_{o} / T_{o}=P_{2} / T_{2}= constant =\rho \cdot \Re\tag{3I.4}\end{align}\)
Different materials warm by different amounts when you add heat. If you know how much thermal energy ∆q you added per kilogram of material, and you measure the resulting increase in temperature T2 – To, then you can empirically determine the specific heat at constant volume:
\(\ \begin{align}C_{v}=\Delta q /\left(T_{2}-T_{o}\right)\tag{3I.5}\end{align}\)
which is about Cv = 717 J·kg–1·K–1 for dry air.
Cp — Specific Heat at Constant Pressure
For a different scenario, consider a box (Figure 3I.3c) with a frictionless moveable piston at the top. The weight of the stationary piston is balanced by the pressure of the gas trapped below it. If you add ∆q thermal energy to the air, the molecules will move faster (Figure 3I.3d), and exert greater pressure against the piston and against the other walls of the chamber. But the weight of the piston hasn’t changed, so the increased pressure of the gas causes the piston to rise.
But when any molecule bounces off the piston and helps move it, the molecule loses some of its microscopic kinetic energy. (An analogy is when a billiard ball bounces off an empty cardboard box sitting in the middle of the billiard table. The box moves a bit when hit by the ball, and the ball returns more slowly.) The result is that the gas temperature T1 in Figure 3I.3e is not as warm as in Figs. 3I.2b or 3I.3d, but is warmer than the initial temperature; namely, To < T1 < T2 .
The molecules spread out within the larger volume in Figure 3I.3e. Thus, air density ρ decreases, causing fewer molecules near the piston to push against it. The combined effects of decreasing density and temperature cause the air pressure to decrease as the piston rises. Eventually the piston stops rising at the point where the air pressure balances the piston weight, as shown in Figure 3I.3e.

Hence, this is an isobaric process (determined by the weight of the piston in this contrived example). The ideal gas law for constant pressure says:
\(\ \begin{align}\rho_{o} \cdot T_{o}=\rho_{1} \cdot T_{1}= constant =P / \Re\tag{3I.6}\end{align}\)
If you know how much thermal energy ∆q you added per kilogram of material, and you measure the resulting increase in temperature T1 – To, then you can empirically determine the specific heat at constant pressure:
\(\ \begin{align}C_{p}=\Delta q /\left(T_{1}-T_{0}\right)\tag{3I.7}\end{align}\)
which is about Cp = 1004 J·kg–1·K–1 for dry air.
Cp vs. Cv
Thus, in a constant pressure situation, the addition of ∆q thermal energy results in less warming [ (T1 – To) < (T2 – To) ] than at constant volume. The reason is that, for constant pressure, some of the random microscopic kinetic energy of the molecules is converted into the macroscale work of expanding the air and moving the piston up against the pull of gravity. Such conservation of energy is partly described by the First Law of Thermodynamics.
In the atmosphere, the pressure at any altitude is determined by the weight of all the air molecules above that altitude (namely, the “piston” is all the air molecules above). If you add a small amount of thermal energy to air molecules at that one altitude, then you haven’t significantly affected the number of molecules above, hence the pressure is constant. Thus, for most atmospheric situations it is appropriate to use Cp , not Cv , when forecasting temperature changes associated with the transfer of thermal energy into or from an air parcel.


