7.4: What does the energy balance of the real atmosphere look like?
- Page ID
- 3392
The real atmosphere's energy balance includes not only radiation energy but also energy associated with evaporation and convection (see figure below). However, the atmosphere is still very close to total energy balance at each level.
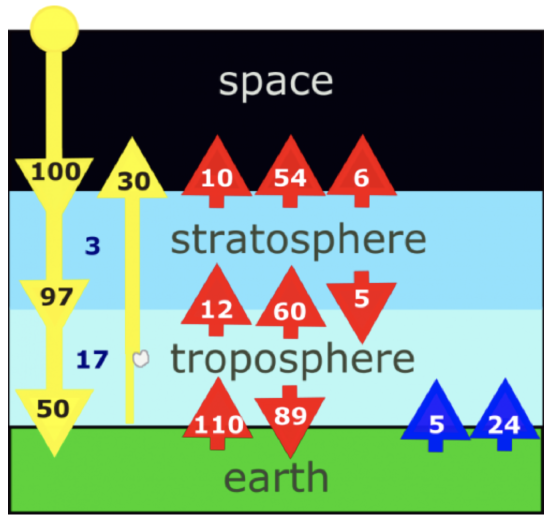
First, let’s go through each set of arrows to see what is happening. The average solar irradiance at the top of the atmosphere is 340.2 W m–2, which we will represent as being 100 units and then compare all other energy amounts to it.
- Leftmost two columns of yellow arrows: Of the solar irradiance coming into the atmosphere, most of the solar ultraviolet irradiance, about 3 units, is absorbed in the stratosphere and warms it, leaving 97 units to make it to the troposphere. 17 units, mostly at wavelengths just longer than solar visible wavelengths, are absorbed in the troposphere and another 30 units are scattered back out to space by bright objects, such as clouds, non-absorbing aerosols, snow, ice, and the land surface, leaving 50 units to be absorbed at Earth’s surface.
- First column of red upward arrows: The Earth’s surface emits upwelling infrared irradiance of 110 units, only 12 units of which are transmitted through the troposphere into the stratosphere, and 10 of these 12 units are subsequently transmitted through the stratosphere to space.
- Second column of red upward arrows: The troposphere radiates 89 units down and 60 units up; 54 of these 60 units escape to space. Unlike our simple two-layer model in which we assumed that the troposphere emitted equally up and down, the real troposphere is more complex and the downward radiation exceeds the upward radiation because of the vertical distribution of temperature (with temperature decreasing with height through the troposphere), water vapor, and carbon dioxide.
- Third column of red upward arrows: The stratosphere radiates 5 units downward and 6 units upward.
- Rightmost blue columns: There is significant non-radiation vertical energy transport at the surface. Of the net 29 units of irradiance absorbed at the Earth’s surface, 24 units go into latent heat. Latent heat quantifies the amount of irradiance necessary to evaporate liquid water (mostly seawater) at Earth’s surface to water vapor. This water vapor is transported upward by convection to form clouds, which releases this energy into the troposphere, warming it. The remaining 5 units of net irradiance absorbed by the surface goes into sensible heat. Sensible heat is the conduction of energy between the warmer Earth’s surface and the cooler tropospheric air, thus warming the air and causing it to become less dense (higher virtual temperature) than its surrounding air, followed by convection, which moves warmer air upward.
At each level, the amount of energy going down must equal the amount of energy going up. Thus, at the top of the stratosphere, 100 units cross into the stratosphere from space, and to balance this downward energy are 30 units of reflected solar irradiance upward to space and 70 units upward emitted infrared radiation that makes it to space. At the top of the troposphere, the downelling of 97 units of solar irradiance and 5 units of infrared irradiance is balanced by the upwelling of 30 units of reflected solar irradiance and 72 units of infrared irradiance. At Earth’s surface, the downward fluxes of solar irradiance (50 units) and infrared irradiance (89 units) balance the upward fluxes of 110 units infrared irradiance, the 24 units of latent heat, and the 5 units of sensible heat.
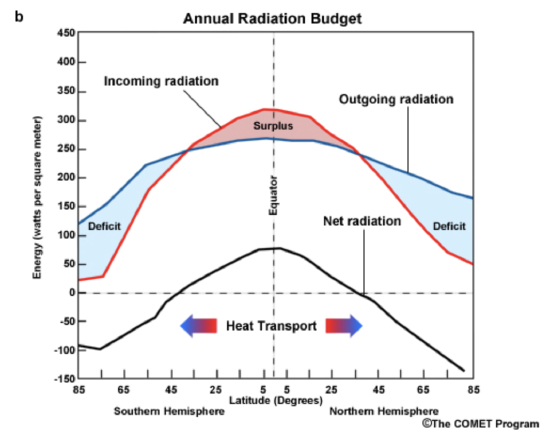
In reality, the Earth’s surface and atmosphere are not in simple radiative equilibrium, but are instead in radiative–convective equilibrium. Furthermore, the atmosphere is in radiative–convective equilibrium globally, but not locally (see figure below). The absorbed solar irradiance is much greater near the equator than the poles because that is where the surface is most perpendicular to the incoming solar irradiance. The radiative and convective net upward energy transport is greatest at the equator as well (because Earth’s surface is warmer there than at the poles). Overall, there is significant net incoming radiation energy between 30oS and 30oN latitude and a net outgoing radiation energy poleward of 30o in both hemispheres.
This uneven distribution of incoming and outgoing radiation results in a flow of energy from the tropics to the poles (see figure below). It unleashes forces that cause warm air to move poleward and cold air to move equatorward. The poleward motion of warmer air, coupled with the Coriolis force that curves moving air to the right in the Northern Hemisphere and to the left in the Southern Hemisphere, causes the atmosphere’s basic wind structure, and thus its weather. We'll talk more about these forces and the resulting motion in the next few lessons when we discuss atmospheric motion (kinematics) and the forces (dynamics) that cause the motion that results in weather.
A series of slides shows you the vertical energy balance in the Earth system and can be found at this site that depicts the energy balance.


