6.4: How is energy related to the wavelength of radiation?
- Page ID
- 3385
We can think of radiation either as waves or as individual particles called photons. The energy associated with a single photon is given by
\[E = hν \]
where \(E\) is the energy (SI units of J), h is Planck's constant (h = 6.626 x 10–34 J s), and \(\nu\) is the frequency of the radiation (SI units of s–1 or Hertz, Hz) (see figure below). Frequency is related to wavelength by \(λ=c/ν\), where \(c\), the speed of light, is 2.998 x 108 m s–1. Another quantity that you will often see is wavenumber, \(σ=1/λ\), which is commonly reported in units of cm–1.
The energy of a single photon that has the wavelength \(λ\) is given by:
\[E=\frac{h c}{\lambda}=\frac{1.986 \times 10^{-16} \mathrm{J} \,\mathrm{nm} \text { photon }^{-1}}{\lambda}\]
Note that as the wavelength of light gets shorter, the energy of the photon gets greater. The energy of a mole of photons that have the wavelength \(λ\) is found by multiplying the above equation by Avogadro's number:
\[E_{m}=\frac{h c N_{A}}{\lambda}=\frac{1.196 \times 10^{8} \mathrm{J} \mathrm{nm} \mathrm{mol}^{-1}}{\lambda}\]
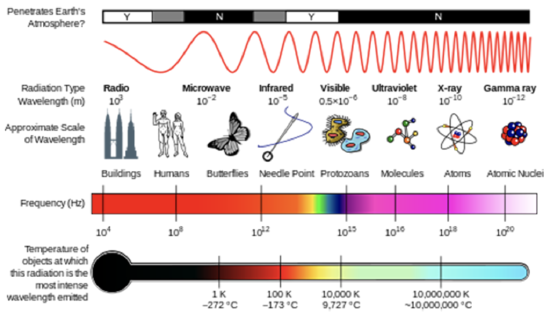
In the lesson on atmospheric composition, you saw how solar UV radiation was able to break apart molecules to initiate atmospheric chemistry. These molecules are absorbing the energy of a photon of radiation, and if that photon energy is greater than the strength of the chemical bond, the molecule may break apart.
Exercise
Consider the reaction
\[\ce{O3 + UV -> O2 + O*}. \nonumber\]
If the bond strength between O2 and O* (i.e., excited state oxygen atom) is 386 kJ mol–1, what is the longest wavelength that a photon can have and still break this bond?
- Click for answer.
-
ANSWER: Solve for wavelength in equation [6.2b]
\(\lambda=\frac{1.196 \times 10^{8} \mathrm{J} \mathrm{nm} \mathrm{mol}^{-1}}{E_{m}}=\frac{1.196 \times 10^{8} \mathrm{J} \mathrm{nm} \mathrm{mol}^{-1}}{386 \times 10^{3} \mathrm{Jmol}^{-1}}=309 \mathrm{nm}\)


