12.5: Frontogenesis
- Page ID
- 9607
Fronts are recognized by the rapid change in surface temperature across the frontal zone. Hence, the horizontal temperature gradient (temperature change per distance across the front) is one measure of frontal strength. Usually potential temperature is used instead of temperature to simplify the problem when vertical motions can occur.
Physical processes that tend to increase the potential-temperature gradient are called frontogenetic — literally they cause the birth or strengthening of the front. Frontogenesis can be caused by kinematic, thermodynamic, and dynamic processes.
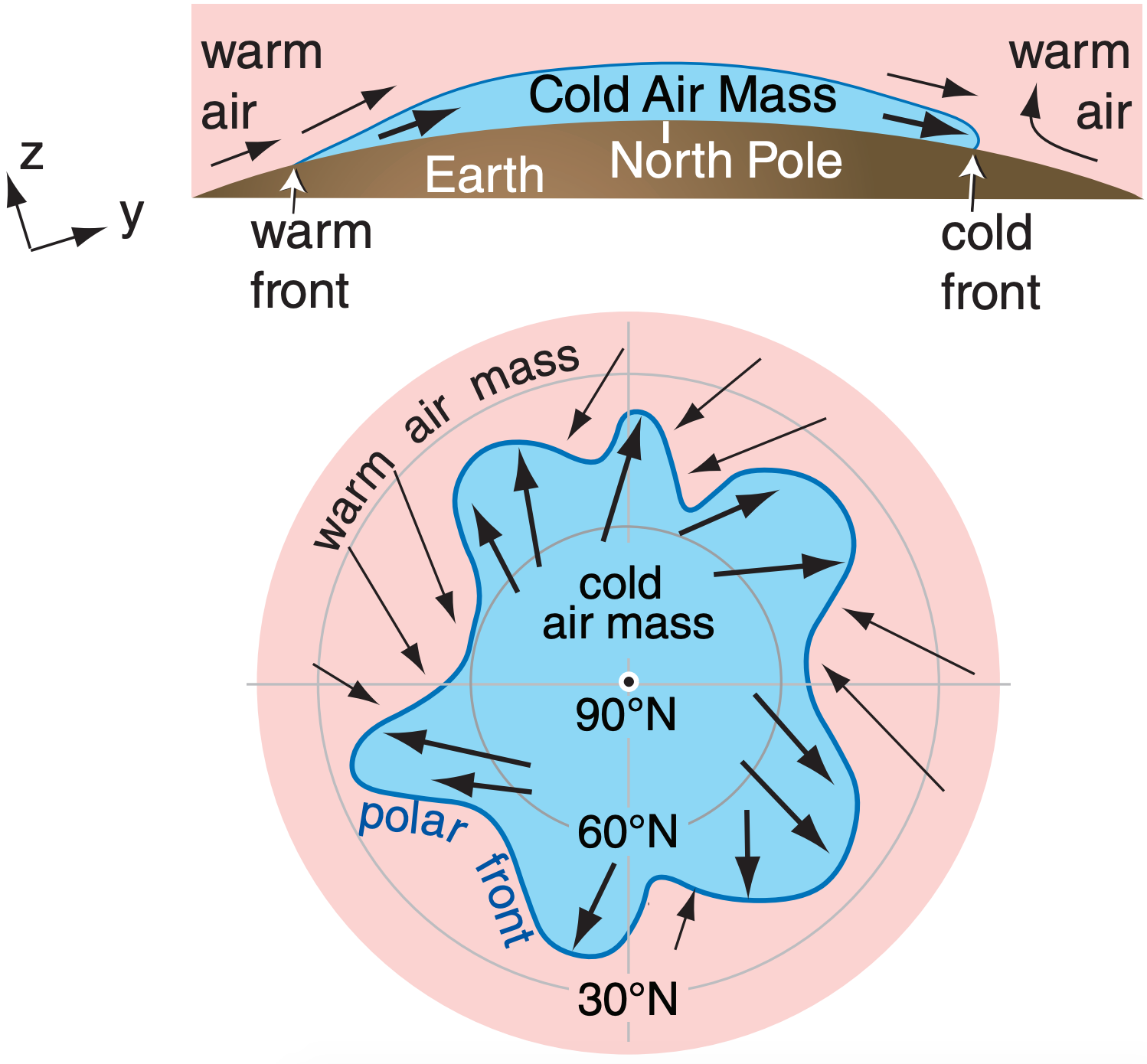
Because of Coriolis force, cold arctic air cannot spread far from the poles, causing a quasi-permanent frontal boundary in the winter hemisphere. This is called the polar front.
It has a wavy irregular shape where some segments advance as cold fronts, other segments retreat as warm fronts, some are stationary, and others are weak and cause gaps in the front.
12.5.1. Kinematics
Kinematics refers to motion or advection, with no regard for driving forces. This class of processes cannot create potential-temperature gradients, but it can strengthen or weaken existing gradients.
From earlier chapters, we saw that radiative heating causes north-south temperature gradients between the equator and poles. Also, the general circulation causes the jet stream to meander, which creates transient east-west temperature gradients along troughs and ridges. The standard-atmosphere also has a vertical gradient of potential temperature in the troposphere (θ increases with z). Thus, it is fair to assume that temperature gradients often exist, which could be strengthened during kinematic frontogenesis.
To illustrate kinematic frontogenesis, consider an initial potential-temperature field with uniform gradients in the x, y, and z directions, as sketched in Fig. 12.21. The gradients have the following signs (for this particular example):
\(\ \begin{align} \frac{\Delta \theta}{\Delta x}=+\quad \frac{\Delta \theta}{\Delta y}=-\quad \frac{\Delta \theta}{\Delta z}=+\tag{12.8}\end{align}\)
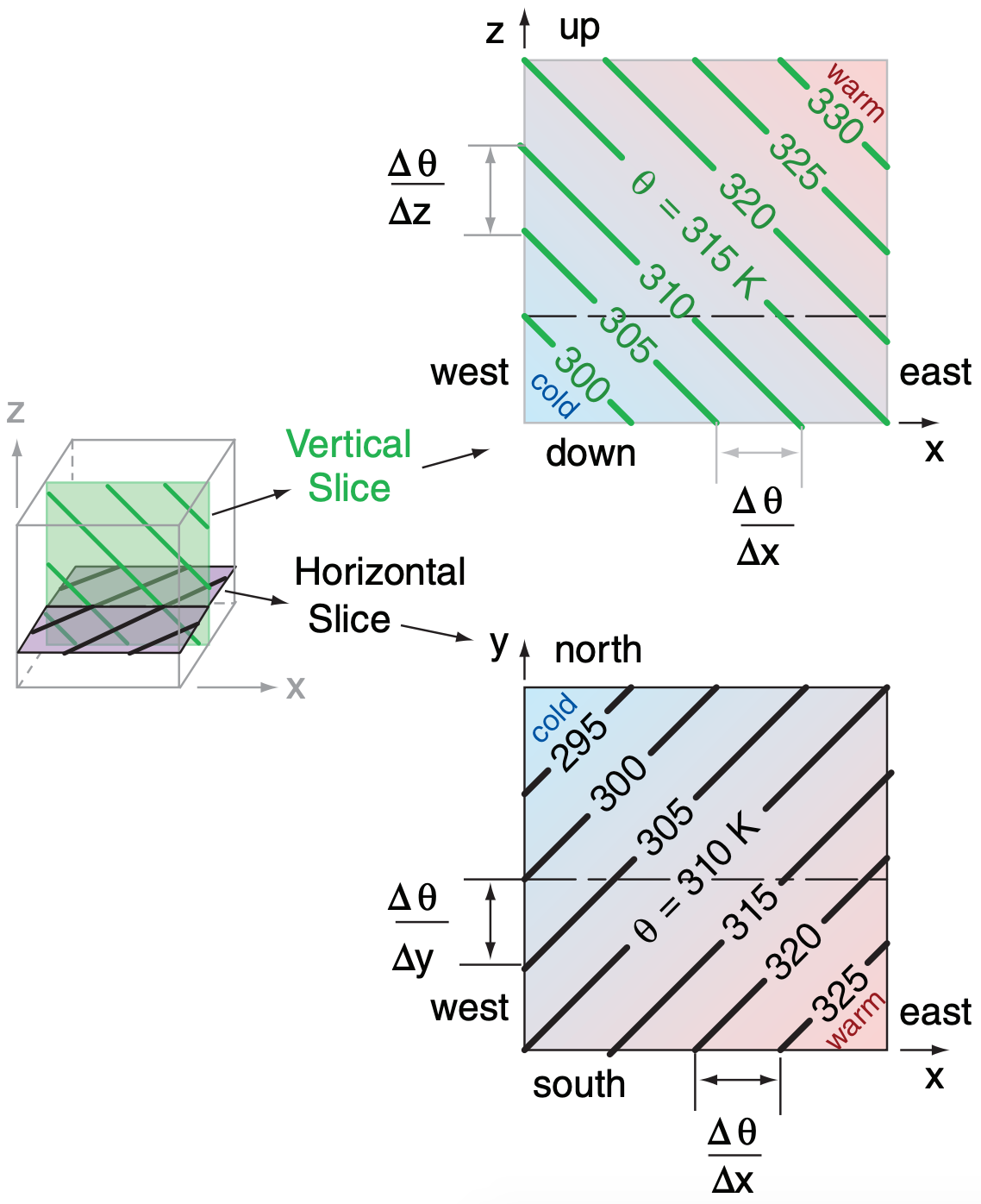
Namely, potential temperature increases toward the east, decreases toward the north, and increases upward. There are no fronts in this picture initially.
We will examine the subset of advections that tends to create a cold front aligned north-south. Define the strength of the front as the potential-temperature gradient across the front:
\(\ \begin{align} \text{Frontal Strength} =F S=\frac{\Delta \theta}{\Delta x}\tag{12.9}\end{align}\)
The change of frontal strength with time due to advection is given by the kinematic frontogenesis equation:
\(\frac{\Delta(F S)}{\Delta t}=-\left(\frac{\Delta \theta}{\Delta x}\right) \cdot\left(\frac{\Delta U}{\Delta x}\right)-\left(\frac{\Delta \theta}{\Delta y}\right) \cdot\left(\frac{\Delta V}{\Delta x}\right)-\left(\frac{\Delta \theta}{\Delta z}\right) \cdot\left(\frac{\Delta W}{\Delta x}\right)\)

12.5.1.1. Confluence
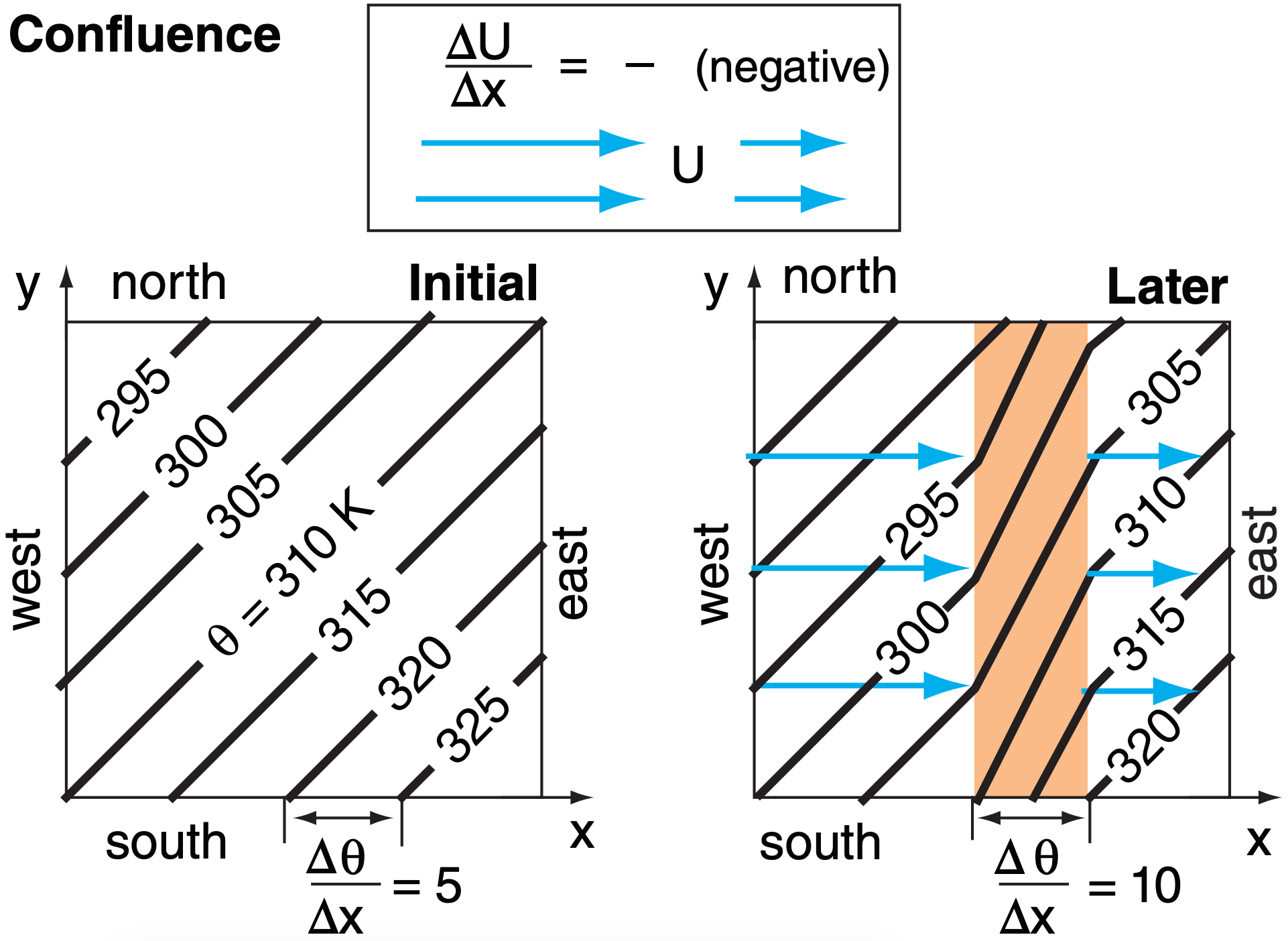
Suppose there is a strong west wind U approaching from the west, but a weaker west wind departing at the east (Fig. 12.22 top). Namely, the air from the west almost catches up to air in the east.
For this situation, ∆U/∆x is negative , and ∆θ/∆x is positive in eq. (12.10). Hence, the product of these two terms, when multiplied by the negative sign attached to the confluence term, tends to strengthen the front [∆(FS)/∆t is positive ]. In the shaded region of Fig. 12.22, the isentropes are packed closer together; namely, it has become a frontal zone.
12.5.1.2. Shear
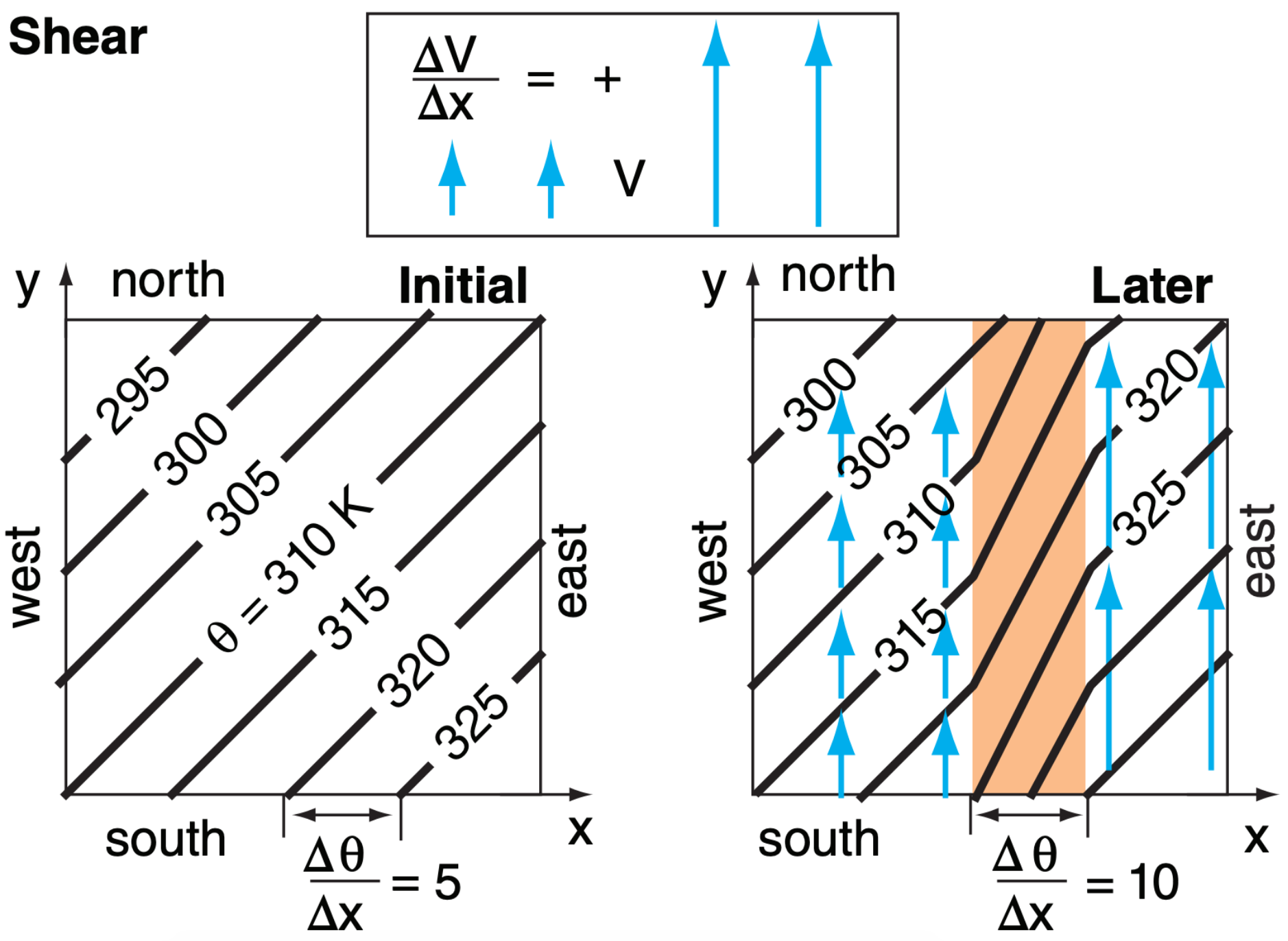
Suppose the wind from the south is stronger on the east side of the domain than the west (Fig. 12.23 top). This is one type of wind shear. As the isentropes on the east advect northward faster than those on the west, the potential-temperature gradient is strengthened in-between, creating a frontal zone.
While the shear ∆V/∆x is positive, the northward temperature gradient ∆θ/∆y is negative. Thus, the product is positive when the preceding negative sign from the shear term is included. Frontal strengthening occurs for this case [∆(FS)/∆t is positive ].
12.5.1.3. Tilting
If updrafts are stronger on the cold side of the domain than the warm side, then the vertical potential-temperature gradient will be tilted into the horizontal. The result is a strengthened frontal zone (Fig. 12.24).
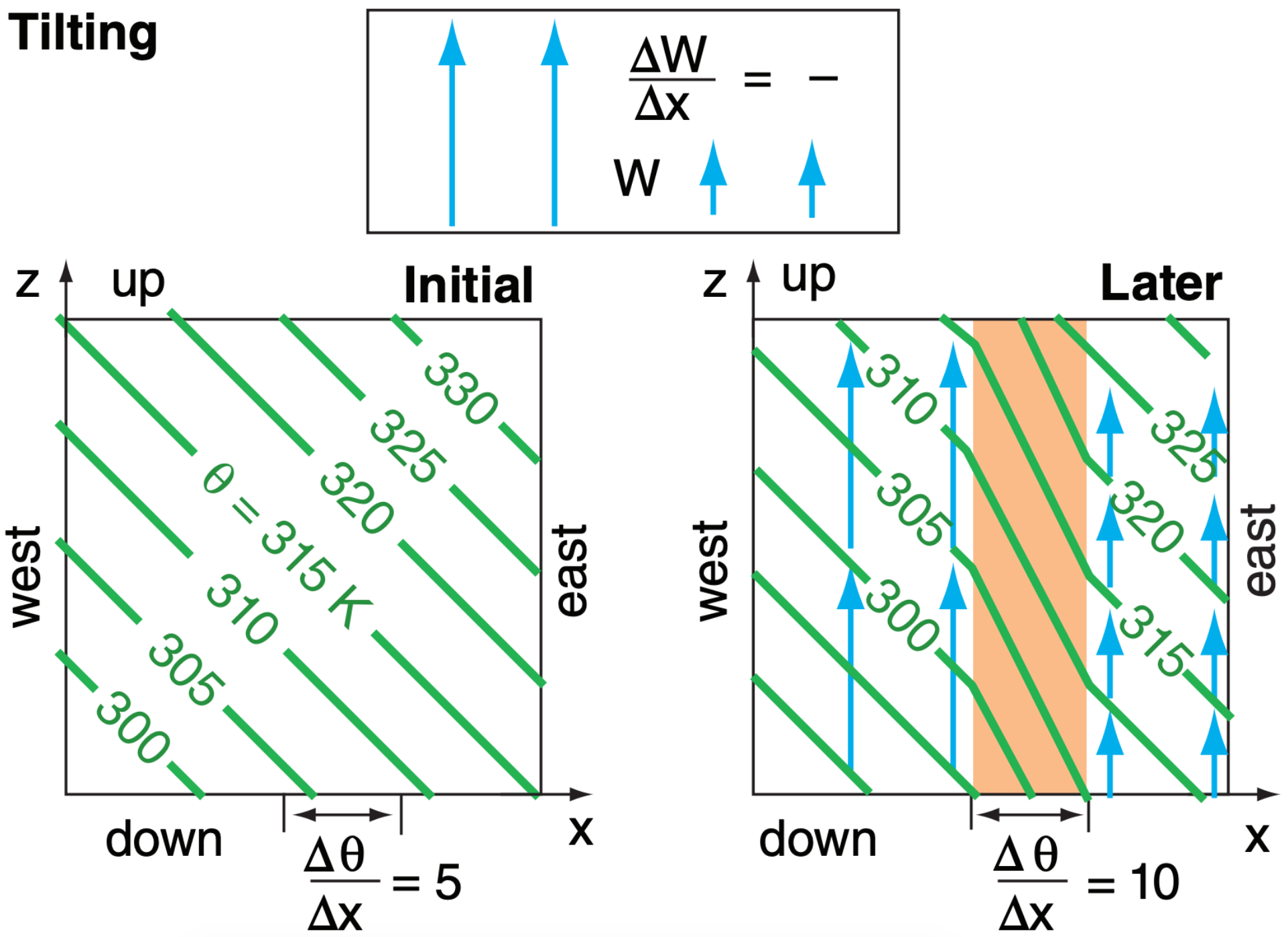
The horizontal gradient of updraft velocity is negative in this example (∆W/∆x = – ), while the vertical potential-temperature gradient is positive (∆θ/∆z = + ). The product, when multiplied by the negative sign attached to the tilting term, yields a positive contribution to the strengthening of the front for this case [∆(FS)/∆t = + ].
While this example was contrived to illustrate frontal strengthening, for most real fronts, the tilting term causes weakening. Such frontolysis is weakest near the surface because vertical motions are smaller there (the wind cannot blow through the ground).
Tilting is important and sometimes dominant for upper-level fronts, as described later.
12.5.1.4. Deformation
The previous figures presented idealized kinematic scenarios. Often in real fronts the flow field is a more complex combination of scenarios. For example, Fig. 12.25 shows a deformation (change of shape) flow field in the cold air, with confluence ( → ← coming together horizontally) of air perpendicular to the front, and diffluence ( ← → horizontal spreading of air) parallel to the front.
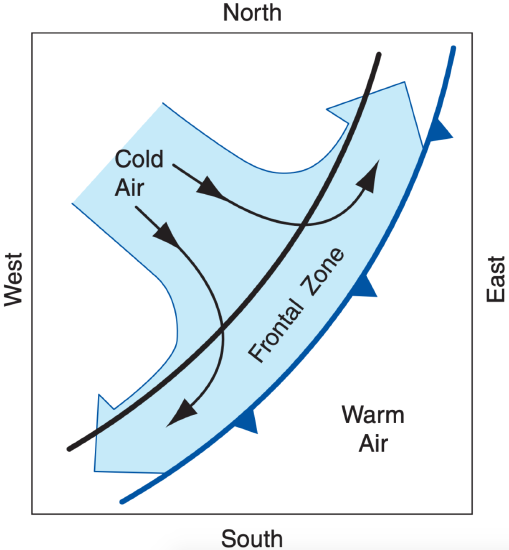
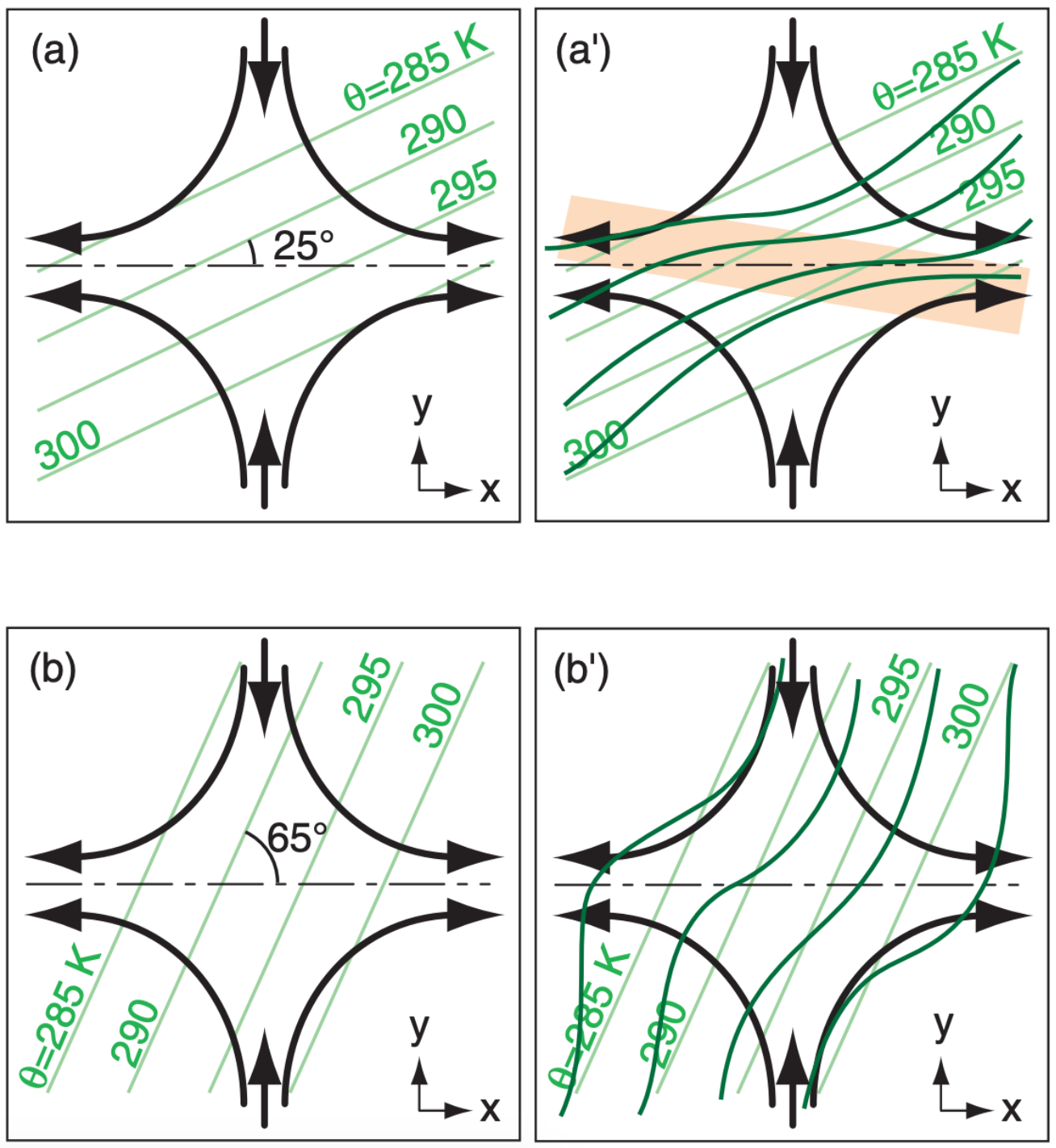
In such a flow field both convergence and shear affect the temperature gradient. For example, consider the two identical deformation fields in Figs. 12.26a & b, where the only difference is the angle of the isentropes in a frontal zone relative to the axis of dilation (the line toward which confluence points, and along which diffluence spreads).
For initial angles less than 45° (Fig. 12.26a & a’), the isentropes are pushed closer together (frontogenesis) and tilted toward a shallower angle. For initial angles greater than 45°, the isentropes are spread farther apart (frontolysis) and tilted toward a shallower angle. Using this info to analyze Fig. 12.25 where the isentropes are more-or-less parallel to the frontal zone (i.e., initial angle << 45°), we would expect that flow field to cause frontogenesis.
Sample Application
Given an initial environment with ∆θ/∆x = 0.01°C km–1, ∆θ/∆y = –0.01°C km–1, and ∆θ/∆z = 3.3°C km–1. Also, suppose that ∆U/∆x = – 0.05 (m/s) km–1, ∆V/∆x = 0.05 (m/s) km–1, and ∆W/∆x = 0.02 (cm/s) km–1. Find the kinematic frontogenesis rate.
Find the Answer
Given: (see above)
Find: ∆(FS)/∆t = ? °C·km–1·day–1
Use eq. (12.10):
\(\begin{aligned} \frac{\Delta(F S)}{\Delta t}=&-\left(0.01 \frac{^{\circ} \mathrm{C}}{\mathrm{km}}\right) \cdot\left(-0.05 \frac{\mathrm{m} / \mathrm{s}}{\mathrm{km}}\right)-\left(-0.01 \frac{^{\circ} \mathrm{C}}{\mathrm{km}}\right)\cdot \left(0.05 \frac{\mathrm{m} / \mathrm{s}}{\mathrm{km}}\right)-\left(3.3 \frac{^{\circ} \mathrm{C}}{\mathrm{km}}\right) \cdot\left(0.0002 \frac{\mathrm{m} / \mathrm{s}}{\mathrm{km}}\right) \end{aligned}\)
= +0.0005 + 0.0005 – 0.00066 °C·m·s–1·km–2
= +0.029 °C·km–1·day–1
Check: Units OK. Physics OK.
Exposition: Frontal strength ∆θ/∆x nearly tripled in one day, increasing from 0.01 to 0.029 °C km–1.
Consider two neighboring streams of air, both moving in nearly the same dominant wind direction. Confluence is when those two streams become closer together. Diffluence is when the streams move further apart. Confluence/diffluence is analogous to streams of cars merging as they enter/exit an expressway or autobahn. In confluent flow, air is converging in a direction perpendicular to the dominant flow direction. Diffluence and divergence are similarly related.
12.5.2. Thermodynamics
The previous kinematic examples showed adiabatic advection (potential temperature was conserved while being blown with the wind). However, diabatic (non-adiabatic) thermodynamic processes can heat or cool the air at different rates on either side of the domain. These processes include radiative heating/cooling, conduction from the surface, turbulent mixing across the front, and latent heat release/absorption associated with phase changes of water in clouds.
Define the diabatic warming rate (DW) as:
\(\ \begin{align} \text{Diabatic Warming Rate} =D W=\frac{\Delta \boldsymbol{\theta}}{\Delta t}\tag{12.11}\end{align}\)
If diabatic heating is greater on the warm side of the front than the cold side, then the front will be strengthened:
\(\ \begin{align} \frac{\Delta(F S)}{\Delta t}=\frac{\Delta(D W)}{\Delta x}\tag{12.12}\end{align}\)
In most real fronts, turbulent mixing between the warm and cold sides weakens the front (i.e., causes frontolysis). Conduction from the surface also contributes to frontolysis. For example, behind a cold front, the cold air blows over a usually-warmer surface, which heats the cold air (i.e., airmass modification) and reduces the temperature contrast across the front. Similarly, behind warm fronts, the warm air is usually advecting over cooler surfaces.
Over both warm and cold fronts, the warm air is often forced to rise. This rising air can cause condensation and cloud formation, which strengthen fronts by warming the already-warm air.
Radiative cooling from the tops of stratus clouds reduces the temperature on the warm side of the front, contributing to frontolysis of warm fronts. Radiative cooling from the tops of post-cold frontal stratocumulus clouds can strengthen the front by cooling the already-cold air.
Sample Application
A thunderstorm on the warm side of a 200 km wide front rains at 2 mm h–1. Find the frontogenesis rate.
Find the Answer
Given: RR = 0 at x = 0, and RR = 2 mm h–1 at x = 200 km
Find: ∆(FS)/∆t = ? °C·km–1·day–1
From the Heat chapter:
∆θ/∆t = (0.33°C mm–1)·RR = 0.66°C h–1.
Combine eqs. (12.11) & (12.12): ∆(FS)/∆t = ∆(∆θ/∆t)/∆x
∆(FS)/∆t = [(0.66°C h–1)·(24 h day–1) – 0] / [200 km – 0] = (15.84°C day–1)/(200km) = 0.079 °C·km–1·day–1
Check: Units OK. Physics OK. Magnitude good.
Exposition: This positive value indicates thermodynamic frontogenesis.
12.5.3. Dynamics
Kinematics and thermodynamics are insufficient to explain observed frontogenesis. While kinematic frontogenesis gives doubling or tripling of frontal strength in a day (see previous Sample Applications), observations show that frontal strength can increase by a factor of 15 during a day. Dynamics can cause this rapid strengthening.
Because fronts are long and narrow, we expect along-front flow to tend toward geostrophy, while across front flows could be ageostrophic. We can anticipate this by using the Rossby number (see INFO Box in the Forces & Winds chapter). Fronts can be of order 1000 km long, but of order 100 km wide. Thus, the Rossby number for along-front flow is of order Ro = 0.1 . But the across-front Rossby number is of order Ro = 1. Recall that flows tend toward geostrophy when Ro < 1. Thus, ageostrophic dynamics are anticipated across the front, as are illustrated next.

Picture an initial state in geostrophic equilibrium with winds parallel to the front, as sketched in Fig. 12.27. This figure shows a special situation where pressure gradients and geostrophic winds exist only midway between the left and right sides. Zero gradients and winds are at the left and right sides. A frontal zone is in the center of this diagram.

Suppose some external forcing such as kinematic confluence due to a passing Rossby wave causes the front to strengthen a small amount, as sketched in Fig. 12.28a. Not only does the potential-temperature gradient tighten, but the pressure gradient also increases due to the hypsometric relationship.
The increased pressure gradient implies a different, increased geostrophic wind. However, initially, the actual winds are slower due to inertia, with magnitude equal to the original geostrophic speed.

While the actual winds adjust toward the new geostrophic value, they temporarily turn away from the geostrophic direction (Fig. 12.29) due to the imbalance between pressure-gradient and Coriolis forces. During this transient state (b), there is a component of wind in the x-direction (Fig. 12.28b). This is called ageostrophic flow, because there is no geostrophic wind in the x-direction.
Because mass is conserved, horizontal convergence and divergence of the U-component of wind cause vertical circulations. These are thermally direct circulations, with cold air sinking and warm air rising and moving over the colder air. The result is a temporary cross-frontal, or transverse circulation called a Sawyer-Eliassen circulation. The updraft portion of the circulation can drive convection, and cause precipitation.
The winds finally reach their new equilibrium value equal to the geostrophic wind. In this final state, there are no ageostrophic winds, and no crossfrontal circulation. However, during the preceding transient stage, the ageostrophic cross-frontal circulation caused extra dynamic confluence near the surface, which adds to the original kinematic confluence to strengthen the surface front. The transverse circulation also tilts the front (Fig. 12.28c).
In summary, a large and relatively steady geostrophic wind blows parallel to the front (Fig. 12.27). A weak, transient, cross-frontal circulation can be superimposed (Fig. 12.28b). These two factors are also important for upper-tropospheric fronts, as described later.


