7.1: Supersaturation and Water Availability
- Page ID
- 9568
7.1.1. Supersaturation
When there is more water vapor in the air than it can hold at equilibrium, the air is said to be supersaturated. Supersaturated air has relative humidity RH greater than 100%. Define this excess relative humidity as a supersaturation fraction S:
\(\ \begin{align} S=R H-1\tag{7.1}\end{align}\)
or as a supersaturation percentage S%:
\(\ \begin{align} S \%=100 \% \cdot S=R H \%-100 \%\tag{7.2}\end{align}\)
Using the definition of relative humidity from the Water Vapor chapter, rewrite supersaturation in terms of total vapor pressure e and saturation vapor pressure es:
\(\ \begin{align} S=\frac{e}{e_{S}}-1\tag{7.3}\end{align}\)
for e > es. It can also be approximated using mixing ratios:
\(\ \begin{align} S \approx \frac{r}{r_{S}}-1\tag{7.4}\end{align}\)
for r > rs.
7.1.2. Water Availability
Suppose that an initially-unsaturated air parcel has total water mixing ratio of rT. If the air parcel rises adiabatically (i.e., no mixing with the environment, and no precipitation in or out), then it cools and its saturation mixing ratio decreases. You can use a thermo diagram (from the Atmospheric Stability chapter) to find these changing mixing ratios, as sketched here in Fig. 7.2.
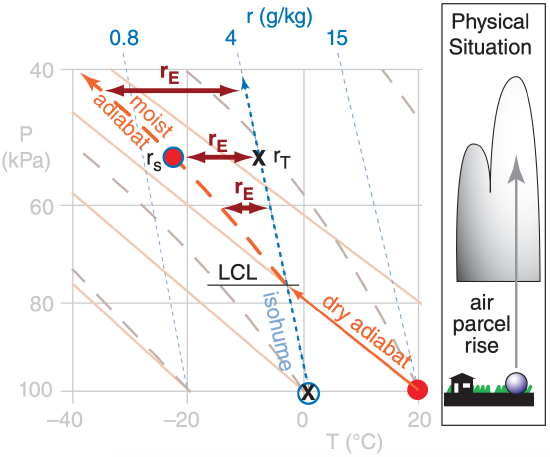
Above the parcel’s lifting condensation level (LCL) the saturation mixing ratio rs is less than rT. This supersaturated air has an excess water mixing ratio rE of:
\(\ \begin{align} r_{E}=r_{T}-r_{s}\tag{7.5}\end{align}\)
The excess water is available to condense onto liquid drops and to deposit onto ice crystals:
\(\ \begin{align} r_{L}+r_{i}=r_{E}\tag{7.6}\end{align}\)
where rL is liquid-water mixing ratio, and ri is ice mixing ratio. At temperatures T in the range –40 < T < 0°C, supercooled liquid water and ice crystals can co-exist in the air.
Available supersaturation fraction is defined as:
\(\ \begin{align} S_{A}=\frac{r_{E}}{r_{S}}=\frac{r_{T}}{r_{S}}-1\tag{7.7}\end{align}\)
As hydrometeors grow and remove water vapor, r becomes less than rT, and S becomes less than SA. Droplets and ice crystals stop growing by condensation and deposition when they have consumed all the available supersaturation (i.e., when r → rs and S → 0).
The adiabatic estimate of rE increases with height above the LCL, as sketched in Figs. 7.2 and 7.3. However, in many real clouds, diabatic (i.e., non-adiabatic) processes such as entrainment and mixing of clear drier air into the top and sides of the cloud cause the total-water mixing ratio to not be conserved with height. As a result, typical amounts of excess-water mixing ratio are less than adiabatic (dashed lines in Fig. 7.3).
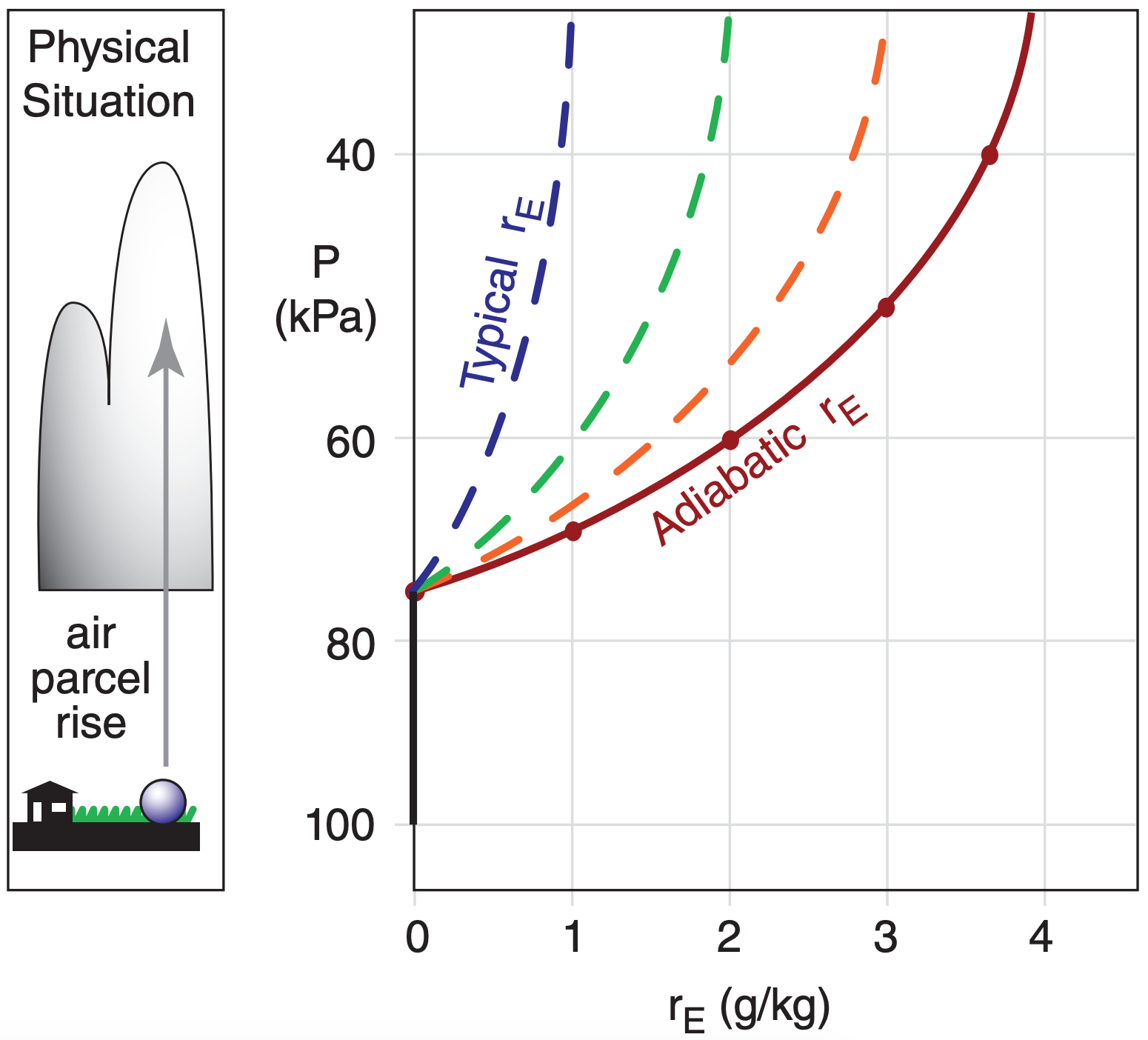
Beware that the adiabatic rE curve varies from situation to situation, depending on the thermodynamic initial conditions of the air parcel. So Fig. 7.3 is just one example (based on the Fig. 7.2 scenario).
Sample Application
An air parcel starts at 100 kPa with temperature 20°C and mixing ratio 4 g kg–1. Use a thermo diagram to find the adiabatic value of excess-water mixing ratio when the parcel reaches a pressure of 60 kPa, and find the max available supersaturation.
Find the Answer
Given: Initially r = rT = 4 g kg–1, T = 20°C, P = 100 kPa
Finally: P = 60 kPa.
Find: rE = ? g kg–1, SA = ? (dimensionless)
Use a full size thermo diagram from the Atmospheric Stability chapter. Starting with the initial conditions, and following the air parcel up dry-adiabatically from the surface, we find the LCL is at P = 75 kPa and T = –3°C, which marks cloud-base. Above the LCL, follow the moist adiabat, which gives T ≈ –15°C at rs = 2 g kg–1 at P = 60 kPa. Assuming no entrainment and mixing, rT = 4 g kg–1.
Use eq. (7.5): rE = (4 – 2) g kg–1 = 2 g kg–1.
Then use eq. (7.7): SA = rE/rs = 1 = 100%.
Check: Units OK. Physics OK. Agrees with Figs. 7.2 & 7.3)
Exposition: A supersaturation of 100% corresponds to a relative humidity of RH = 200% from eq. (7.2). Thus, there is twice as much water in the air as can be held at equilibrium. This excess water vapor drives condensation. For real clouds, we expect rE in the range of 0.5 to 1.5 g kg–1, based on the curves in Fig. 7.3.
7.1.3. Number and Size of Hydrometeors
Suppose we partition the available excess water equally between all hydrometeors (for example, for all liquid water droplets). In this way, we can estimate the average radius R for each droplet due only to condensation (i.e., before collisions between droplets allow some to merge and grow into larger drops):
\(\ \begin{align} R=\left[\frac{3}{4 \pi} \cdot \frac{\rho_{a i r}}{\rho_{\text {water}}} \cdot \frac{r_{E}}{n}\right]^{1 / 3}\tag{7.8}\end{align}\)
where excess-water mixing ratio rE is in kgwater kgair–1, ρ is density, and n is the number density of hydrometeors (the count of hydrometeors per cubic meter of air). Typical values are R = 2 to 50 µm, which is small compared to the 1000 µm separation between droplets, and is too small to be precipitation.
This is an important consideration. Namely, even if we ignore the slowness of the diffusion process (described later), the hydrometeors stop growing by condensation or deposition before they become precipitation. The reason is that there are too many hydrometeors, all competing for water molecules, thus limiting each to grow only a little.
The number density n of hydrometeors is initially controlled by the number density of nuclei upon which they can form, as described next.
Sample Application
Within a cloud, suppose air density is 1 kg m–3 and the excess water mixing ratio is 4 g kg–1. Find the final drop radius for hydrometeor counts of (a) 108 m–3, and (b) 109 m–3.
Find the Answer
Given: rE = 0.004 kgwater kgair–1, ρair = 1 kg m–3 n = (a) 108 m–3, and (b) 109 m–3.
Find: R = ? µm
Assume: ρwater = 1000 kg m–3, as listed in Appendix A.
Use eq. (7.8). Part (a),:
\(\begin{aligned} R &=\left[\frac{3 \cdot\left(1 \mathrm{kg}_{\text {air }} / \mathrm{m}^{3}\right) \cdot\left(0.004 \mathrm{kg}_{\text {water }} / \mathrm{kg}_{\text {air }}\right)}{4 \pi \cdot\left(10^{3} \mathrm{kg}_{\text {water }} / \mathrm{m}^{3}\right) \cdot\left(10^{8} \mathrm{m}^{-3}\right)}\right]^{1 / 3}=2.12 \times 10^{-5} \mathrm{m}=21.2 \mu \mathrm{m} \end{aligned}\)
(b) Similarly, R = 9.8 µm.
Check: Units OK. Physics OK.
Exposition: Both of these numbers are well within the range of “typical” cloud droplets. Thus, the final drop size is NOT large enough to become precipitation.


