4.4: Water Budget at a Fixed Location
- Page ID
- 9551
Picture a cube of air at a fixed location relative to the ground (i.e., an Eulerian framework). Inflow and/or outflow of water (as vapor, liquid, or solid) can change the total water content rT of air inside the hypothetical cube. As we did for heat, we can investigate each inflow and outflow process to determine which are significant. The insignificant ones include turbulent transport in the horizontal, molecular conduction (except close to the ground), and mean vertical advection (except in deep convective storms).
What remains is an approximate equation for the total water budget in an Eulerian framework:
\(\ \begin{align} \frac{\Delta r_{T}}{\Delta t}=-\left[U \cdot \frac{\Delta r_{T}}{\Delta x}+V \cdot \frac{\Delta r_{T}}{\Delta y}\right]+\left(\frac{\rho_{L}}{\rho_{d}}\right) \frac{\Delta P r}{\Delta z}-\frac{\Delta F_{z} \operatorname{turb}\left(r_{T}\right)}{\Delta z}\tag{4.44}\end{align}\)
\(\ \quad \text{storage horiz. advection precipitation turbulence}\)
where precipitation is falling at rate Pr, horizontal advection is caused by wind components (U, V), the turbulent total-water flux (in kinematic units) is Fz turb (rT), and (∆x, ∆y, ∆z, ∆t) are the Cartesian dimensions of the cube and the time interval, respectively.
Define Standard Temperature and Pressure (STP) as T = 0°C and P = 101.325 kPa. Using air density at STP and liquid water density (ρL = 1000 kgliq m–3) from Appendix B, you would find that ρL/ρd = 836.7 kgliq kgair–1, but this value would increase for hypothetical cubes at higher altitudes where air density is smaller .
In the subsections that follow, we will focus on the individual terms in eq. (4.44).
4.5.1. Horizontal Advection
If more total water (vapor + suspended cloud droplets + suspended ice crystals) is blown out of the cube than blows in, then the total water will decrease during time interval ∆t.
4.5.2. Precipitation
Some solid and liquid water particles are large enough that they are not suspended in, and do not move with, the mean winds. Instead, they fall through the air as precipitation. If all the liquid and solid precipitation were collected in a rain gauge and then melted to be all liquid, the resulting water depth is called the liquid water equivalent. Thus, 2 mm of liquid precipitation plus 5 cm of snow (which might reduce to 5 mm of water when melted) would give a total liquid water depth of 7 mm.
If more precipitation falls out of the bottom of the air cube than is falling into the top, then this change of precipitation with altitude would tend to reduce the total water in the cube. Thus, the change of precipitation rate (Pr in mm h–1 or m s–1) between the top and bottom of the cube of air is important.
Not all the precipitation will reach the ground, because some might evaporate on the way down. The liquid-equivalent precipitation rate (Pr) at the ground is called the rainfall rate (RR).
“Reasoning” is the method by which we try to explain how things work. Namely, we try to infer an explanation or a theory that is reasonable. Two types of reasoning are inductive and deductive reasoning.
Characteristics of inductive reasoning:
- Going from specific examples to general theories.
- The general theory may be likely, but not certain
- Often requires a “leap of faith”.
- Could apply to situations not yet encountered.
- Can be proven wrong by new contrary evidence.
- Analogous to extrapolation.
Characteristics of deductive reasoning:
- Applying a general rule to a specific application.
- Confidence that the result is correct and will work well in new situations if used within the bounds of the general rule.
- Is a sound tool used in engineering.
- Analogous to interpolation.
As a contrived example, what if you observed that as adults, your grandparent was 1.4 m tall, your parent was 1.6 m tall, and you are 1.8 m tall. You could deduce that you are 0.2 m taller than your parent. In fact, you would consider this a “truth” based on the logic of mathematics.
However, you could induce that your unborn child will be 2.0 m tall as an adult. Namely, you saw a pattern from past observations: each offspring was 0.2 m taller than its parent. So extrapolating to your future unborn child, you might expect the child to become 0.2 m taller than you.
Obviously this last prediction carries some uncertainty. You could reduce the uncertainty by collecting more evidence from other families, or by going further back in your family tree. However, many factors over which you have little control could alter the growth of your child — your prediction is uncertain.
This same procedure is done by scientists proposing new theories. Namely, gain confidence that your theory is “universal” in the sense that it works at other places and times in the universe. Such a goal motivated Isaac Newton to design and build telescopes, so he could test his theories of motion by looking at other planets in the universe. The evidence convinced scientists to accept Newton’s hypotheses as “laws of motion”, yet they were later proven wrong by Einstein.
Let’s try some inductive reasoning now. Eq. (4.44) says that change of total water depends on horizontal advection, change of turbulent fluxes in the vertical, and other source terms. Eq. (3.51) said that change of temperature depends on horizontal advection, change of turbulent fluxes in the vertical, and other source terms. By inductive reasoning, we might anticipate that the change of momentum (i.e., wind speed) depends on horizontal advection, change of turbulent fluxes in the vertical, and other source terms. We will check this later, in the Forces & Winds chapter.
Sample Application
Precipitation falls out of the bottom of a cloud at rate 0.5 cm h–1. At 200 m below cloud base, the precipitation rate is 0.4 cm h–1. In this 200 m thick layer of air below cloud base, what is the total-water change rate? Assume ρair = 1 kg m–3.
Find the Answer
Given: Prbot = 0.4 cm h–1 = 1.11x10–6 m s–1,
Prtop = 0.5 cm h–1 = 1.39x10–6 m s–1,
ρair = 1 kg m–3, and
∆z = 200 m
Find: ∆rT/∆t = ? (g kg–1)/s.
Because no other processes are specified, let’s neglect them for simplicity. Thus, we can apply eq. (4.44):
∆rT/∆t = (ρL/ρd)·(Prtop–Prbot)/(ztop–zbot) = \(\frac{\left(1.0 \times 10^{6} \mathrm{g}_{\text {water }} / \mathrm{m}^{3}\right)}{\left(1 \mathrm{kg}_{\text {air }} / \mathrm{m}^{3}\right)} \cdot \frac{\left[(1.39-1.11) \times 10^{-6} \mathrm{m} / \mathrm{s}\right]}{200 \mathrm{m}}\)
= 0.0014 (g kg–1)/s = 5 (g kg–1)/h
Check: Physics and units are reasonable.
Exposition: This is typical of virga, a weather element where some of the precipitation evaporates before reaching the ground. In virga, the evaporating rain makes the air more humid below cloud base.
4.5.3. Moisture Flux at the Earth’s Surface
In the previous chapter we discussed ways to estimate sensible and latent heat fluxes at the Earth’s surface. But latent heat flux is tied to the movement of water molecules. Here we show how you can use knowledge of the latent heat flux to estimate the moisture flux at the Earth’s surface.
Recall that vertical flux is the movement of something across a horizontal unit area per unit time. Let FE be the latent heat flux in units of (J·m–2·s–1 or W·m–2) and Fwater be the vertical water-vapor flux in units of (kgwater· m–2·s–1). The relationship between these fluxes is:
\(\ \begin{align} \mathbb{F}_{water}=\mathbb{F}_E/L_v\tag{4.45}\end{align}\)
or
\(\ \begin{align} \mathbb{F}_{water}=\rho_{air} \cdot (C_p/L_v)\cdot F_E \tag{4.46}\end{align}\)
or
\(\ \begin{align} \mathbb{F}_{water}=\rho_{air} \cdot \gamma \cdot F_E\tag{4.47}\end{align}\)
Constants and parameters in these equations are: FE = kinematic latent heat flux (K·m·s–1);
Lv = 2.5x106 J kgwater –1 = latent heat of vaporization;
γ = Cp/Lv = 0.4 (gwater kgair–1)·K–1 = psychrometric constant.
If you divide these equations by air density (ρair.), then you can get the water flux in kinematic form:
\(\ \begin{align} F_{water}=\mathbb{F}_{water}/\rho_{air} \tag{4.48a}\end{align}\)
For example, eq. (4.45) becomes:
\(\ \begin{align} F_{water}=\mathbb{F}_E/(\rho_{air} \cdot L_v)=\gamma \cdot F_E \tag{4.48b}\end{align}\)
The advantage of kinematic water flux (Fwater) is that its units are similar to (mixing ratio) x (wind speed). Thus, the units are (kgwater kgair–1)·(m·s–1).
When water from a puddle on the Earth’s surface evaporates, the puddle depth decreases. The rate of this depth decrease (mm day–1) is the evaporation rate, (Evap), which is related to the moisture flux:
\(\ \begin{align}E_{vap}=\mathbb{F}_{water}/\rho_L = \mathbb{F}_E/(\rho_L \cdot L_v)=a \cdot\mathbb{F_E} \tag{4.49}\end{align}\)
\(\ \begin{align}E_{vap}=(\rho_{air}/\rho_L)\cdot F_{water}=(\rho_{air}/\rho_L)\cdot \gamma \cdot F_E \tag{4.50}\end{align}\)
For these equations, ρL = 1000 kgliq m–3, a = 0.0346 (m2 W–1)·(mm day–1) = 4.0x10–10 m3·W–1·s–1.
Sample Application
Suppose the latent heat flux is 250 W·m–2. What are the values of water-vapor flux, kinematic water-vapor flux and evaporation rate? Assume ρair = 1 kgair m–3.
Find the Answer
Given: ρair = 1 kgair· m–3, FE = 250 W·m–2
Find: Fwater = ? kgwater·m–2·s–1 , Evap = ? mm day–1 , Fwater = ? (kgwater· kgair–1)·(m–2·s–1)
Apply eq. (4.45):
Fwater = (250 J·m–2·s–1)/(2.5x106 J kg–1) = 0.0001 kgwater·m–2·s–1
Apply eq. (4.48a):
Fwater = (0.0001 kgwater·m–2·s–1)/ (1 kgair m–3) = 0.0001 (kgwater· kgair–1)·(m·s–1)
Apply eq. (4.49): Evap = a · FE
= [ 0.0346 (m2 W–1)·(mm day–1)]·( 250 W m–2 ) = 8.65 mm day–1
Check: Physics and units are reasonable. Namely, the first answer has units of water mass per area per time, the second is like a mixing ratio times velocity, and the third is rate of decreased of water depth in a puddle.
Exposition: If this evaporation rate continues day after day, crops could become desiccated.
For windy conditions, another way to estimate the water vapor flux (in kinematic units) is with a bulk-transfer relationship similar to eq. (3.35), such as
\(\ \begin{align} F_{\text {water}}=C_{H} \cdot M \cdot\left(r_{\text {sfc}}-r_{\text {air}}\right)\tag{4.51}\end{align}\)
where the wind speed at 10 m above the surface is M, and the water-vapor mixing ratio in the air at 2 m above the surface is rair. The bulk-transfer coefficient for water vapor is roughly the same as the one for heat, CH, which ranges between 2x10–3 (for smooth surfaces) to 2x10–2 (for rough surfaces).
In calmer conditions with sunny skies, convective thermals of warm rising air can form, which are effective at transporting moisture in the vertical. The resulting kinematic water-vapor flux is:
\(\ \begin{align} F_{\text {water}}=b_{H} \cdot w_{B} \cdot\left(r_{\text {sfc}}-r_{M L}\right)\tag{4.52}\end{align}\)
for a mid-mixed layer mixing ratio of rML and a convective heat-transport coefficient of bH = 5x10–4 (dimensionless). Eq. (3.38) in the previous chapter gives the expression for buoyancy-velocity scale wB.
While the two equations above seem physically reasonable, they have a problem in that the mixing ratio at the surface rsfc (literally at the Earth’s surface skin) is an abstract concept that is not measurable. For the special case of a river or lake surface or rain-saturated ground, scientists often approximate rsfc ≈ rs(Tsfc); namely the surface mixing ratio equals the saturation mixing ratio rs (eq. 4.5) for air at a temperature Tsfc equal to that of the surface skin.
Sample Application
A cold front recently passed over your farm field during which it rained hard, but now it is windy with M = 15 m s–1. Air behind the cold front is relatively dry (r2m = 5 g kg–1), but the ground surface is still relatively warm (14°C). Assume your farm is near sea level. What kinematic water-vapor flux do you expect?
Find the Answer
Given: M = 15 m s–1, rair = 5 g kg–1 , Tsfc = 14°C
Find: Fwater = ? (kgwater kgair–1)·(m·s–1)
The farm field is probably not perfectly smooth, so let’s assume CH ≈ 5x10–3 (dimensionless). But assume the recent rain left the soil nearly saturated with water.
To apply eq. (4.51), we need to estimate rsfc ≈ rs(Tsfc) = rs (14°C) = 10.0 g kg–1 from eqs (4.1) & (4.5). Thus, eq. (4.51) is:
Fwater = (5x10–3 )·(15 m s–1)·(10.0 – 5 g kg–1)
= 0.375 (gwater.kgair)·(m·s–1)
= 0.000375 (kgwater kgair–1)·(m·s–1)
Check: Physics and units are reasonable.
Exposition: If you apply eq. (4.50) you find this is associated with an evaporation rate of 40 mm day–1.
Sample Application
What is the value of Fwater on a sunny day with no winds? Assume mixed-layer depth zi = 3 km, θML = 290 K, and θsfc = 320 K. The air and ground are somewhat dry, so rsfc = 5 g kg–1, and rML = 3 g kg–1.
Find the Answer
Given: rsfc = 5 g kg–1, rML = 3 g kg–1, zi = 3 km, θsfc = 320 K, θML = 290 K
Find: Fwater = ? (kgwater kgair–1)·(m·s–1)
Sunny, calm conditions suggests a convective mixed layer, so we can apply eq. (4.52). The temperature info in this sample application is the same as for a sample application in the Surface Fluxes section of Chapter 3, where we found from eq. (3.38) that wB ≈ 55.1 m s–1.
Thus, eq. (4.52) is:
Fwater = (5x10–4 )·(55.1 m s–1)·(5 – 3 g kg–1)
= 0.055 (gwater.kgair)·(m·s–1)
= 5.5x10–5 (kgwater kgair–1)·(m·s–1)
Check: Physics and units are reasonable.
Exposition: If you apply eq. (4.50) you find this is associated with an evaporation rate of 5.83 mm day–1 at sea level.
4.5.4. Moisture Transport by Turbulence
Recall from the Thermodynamics chapter that turbulence is the quasi-random movement and mixing of air parcels by swirls and eddies — analogous to the effects of an egg beater. By mixing together dry and moist air parcels, turbulence causes a net moisture transport — namely, a moisture flux. If the moisture flux out of the top of a layer of air is different than the moisture flux into the bottom, then there is a moisture flux divergence ∆Fz turb(rT)/∆z that changes the total water content in the layer. For hot sunny days with light winds, rising thermals create a mixed layer of depth zi , within which:
\(\ \begin{align} \frac{\Delta F_\text{z turb}\left(r_{T}\right)}{\Delta z}=\frac{F_\text{zturb at z i}\left(r_{T}\right)-F_\text{z turb at surface}\left(r_{T}\right)}{z_{i}-z_{\text {surface}}}\tag{4.53}\end{align}\)
where eq. (4.53) says that the local flux divergence equals the average flux divergence across the whole turbulent mixed layer (ML).
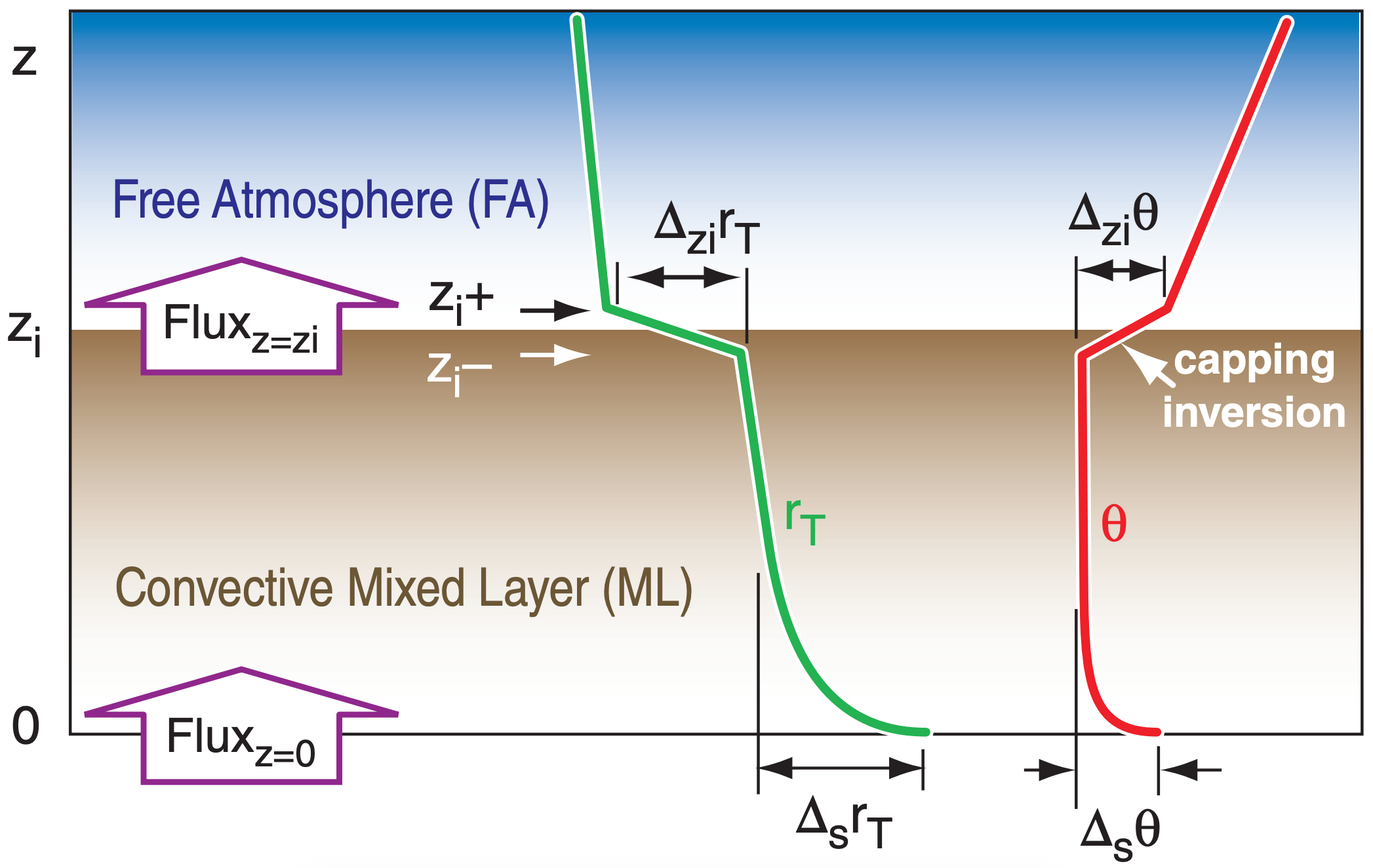
At the top of the ML, entrainment brings in warmer drier air from just above the ML top (at zi +) and mixes it with air just below the ML top (at zi –), see Figure 4.12. That entrainment is driven by thermals associated with the effective surface heat flux FH (in kinematic units of K m s–1) and is modulated by the strength of the capping temperature inversion ∆ziθ, where ∆zi = ( )zi+ – ( )zi– . Thus,
\(\ \begin{align} \frac{\Delta F_\text{z turb}\left(r_{T}\right)}{\Delta z}=-\frac{\left[0.2 \cdot\left(\Delta_{z_{i}} r_{T} / \Delta_{z_{i}} \theta\right) \cdot F_{H}\right]+F_{\text {water}}}{z_{i}}\tag{4.54}\end{align}\)
Also in eq. (4.54) is Fwater, the effective surface water-vapor flux [units kinematic (kgwater kgair–1)· (m s–1) ], which can be rewritten using the psychrometric constant [γ = 0.4 (gwater kgair–1)·K–1] in terms of the latent heat flux FE (eq. 4.48), at the surface:
\(\ \begin{align} \frac{\Delta F_\text{z turb}\left(r_{T}\right)}{\Delta z}=-\frac{0.2 \cdot\left(\Delta_{z_{i}} r_{T} / \Delta_{z_{i}} \theta\right) \cdot F_{H}+\gamma \cdot F_{E}}{z_{i}}\tag{4.55}\end{align}\)
The effective surface sensible and latent heat fluxes in the eq. above can be parameterized using the convective transport coefficient (bH, see the Thermodynamics chapter) and the buoyancy velocity scale wB (see eq. 3.38):
\(\ \begin{align}\frac{\Delta F_\text{z turb}\left(r_{T}\right)}{\Delta z}=-\frac{b_{H} \cdot w_{B}}{z_{i}}\left\{\left[0.2 \cdot\left(\Delta_{z_{i}} r_{T}\right) \cdot\left|\frac{\Delta_{s} \theta}{\Delta_{z_{i}} \theta}\right|\right]+\left|\Delta_s r_T\right|\right\}\tag{4.56}\end{align}\)
where ∆s( ) = ( )surface – ( )mid mixed-layer
Any one of the four eqs. above can be used to find moisture-flux divergence for 0 < z < zi . Above the convective ML (at z > zi ) where turbulence is weak or nonexistent:
\(\ \begin{align} \frac{\Delta F_\text{z turb}\left(r_{T}\right)}{\Delta z} \approx 0 \tag{4.57}\end{align}\)
During night, turbulence is often weak at most heights (except very close to the surface), allowing you to use eq. (4.57) as a reasonable approximation at z > 0.
Next, consider a different type of mixed layer — one that is mixed mechanically by wind shear on windy days (not by thermals on calm sunny days). Further, suppose that there is such a strong capping temperature inversion at the top of this layer (at height zi ) that there is negligible entrainment (thus near zero moisture flux) into the top of this ML. For this case, the turbulent moisture flux divergence is driven solely by Fwater, the flux at the Earth’s surface: ∆Fz turb(rT)/∆z ≈ – Fwater/zi . For example, in winter a humid ML might lose moisture due to condensation of water onto a cold snow-covered landscape. Or a cool dry ML might gain moisture by evaporation from a warm lake.
Thunderstorms are deep convective storms that turbulently mix air over the whole depth of the troposphere. The fuel for such storms is humidity in the prestorm mixed layer. When this ML air is drawn into the storm via the storm updrafts, water vapor condenses and falls out as rain. Meanwhile, drier air from the mid-troposphere is often brought down towards the surface to create a new, but drier, post-storm atmospheric boundary layer (ABL). Some of the falling rain can evaporate into this drier ML, increasing the humidity there.
Sample Application
Winds are light and solar heating is strong, creating a convective mixed layer (ML) having depth 1.5 km and convective transport of bH·wB = 0.03 m s–1. The potential temperature jump near the surface is 7°C while the corresponding jump near the top of the ML is 4°C. The jumps of total water mixing ratio are 6 and –3 g kg–1, respectively. (a) Find the turbulent flux divergence of rT. (b) If that was the only process active, then at what rate does total water increase in the ML?
Find the Answer
Given: zi = 1.5 km = 1500 m, bH·wB = 0.03 m s–1.
|∆sθ| = 7°C, |∆ziθ| = 4°C, |∆srT| = 6 g kg–1, ∆zirT = –3 g kg–1, No other processes acting.
Find: (a) ∆Fz turb(rT)/∆z = ? (g kg–1)/s,
(b) ∆rT/∆t = ? (g kg–1)/s,
(a) Apply eq. (4.56):
\(\begin{aligned} \frac{\Delta F_\text{z turb}\left(r_{T}\right)}{\Delta z}=-\frac{b_{H} \cdot w_{B}}{z_{i}}\left[0.2 \cdot\left(\Delta_{z_{i}} r_{T}\right) \cdot\left|\frac{\Delta_{s} \theta}{\Delta_{z_{i}} \theta}\right|+\left|\Delta_{s} r_ T\right|\right] \\ \quad=-\frac{(0.03 \mathrm{m} / \mathrm{s})}{(1500 \mathrm{m})}\left[0.2 \cdot\left(-3 \frac{\mathrm{g}}{\mathrm{kg}}\right) \cdot\left|\frac{7^{\circ} \mathrm{C}}{\mathrm{kg}}\right|+\left(6 \frac{\mathrm{g}}{\mathrm{kg}}\right)\right] \\=&-9.9 \times 10^{-5}\left(\mathrm{g} \mathrm{kg}^{-1}\right) / \mathrm{s} \end{aligned}\)
(b) Apply eq. (4.44):
∆rT/∆t = – ∆Fz turb(rT)/∆z = 9.9x10–5 (g kg–1)/s = 0.36 (g kg–1)/hour
Check: Physics and units are reasonable.
Exposition: Entrainment is bringing dry air down into the mixed layer [F(rT) = – ], but that drying rate is offset by moisture flux entering the ML from the Earth’s surface, leading to increase of rT with time.


