3.7: Apparent Temperature Indices
- Page ID
- 9870
Warm-blooded (homeothermic) animals including humans generate heat internally via metabolism of the food we eat with the oxygen we breathe. But we also rely on heat transfer with the environment to help maintain an internal core temperature of about 37°C (= 98.6°F). (Our skin is normally cooler — about 33.9°C = 93°F). Heat transfer occurs both via sensible heat fluxes (temperature difference between air and our skin or lungs) and latent heat fluxes (evaporation of moisture from our lungs and of perspiration from our skin).
The temperature we “feel” on our skin depends on the air temperature and wind speed (as they both control the bulk heat transfer between our skin and the environment) and on humidity (is it affects how rapidly perspiration evaporates to cool us).
Define a reference state as being a person walking at speed Mo = 4.8 km h–1 through calm, moderately dry air. The actual air temperature is defined to be the temperature we “feel” for this reference state.
The apparent temperature is the temperature of a reference state that feels the same as it does for non-reference conditions. For example, faster winds in winter make the temperature feel colder (wind chill) than the actual air temperature, while higher humidities in summer make the air feel warmer (humidex or heat index).
3.7.1. Wind-Chill Temperature
The wind-chill temperature index is a measure of how cold the air feels to your exposed face. The official formula, as revised in 2001 by the USA and Canada, for wind chill in °C is:
\(\ \begin{align}T_{\text {wind chill }}=\left(a \cdot T_{\text {air}}+T_{1}\right)+\left(b \cdot T_{\text {air}}-T_{2}\right) \cdot\left(\frac{M}{M_{o}}\right)^{0.16} for\ M>M_{o}\tag{3.64a}\end{align}\)
or
\(\ \begin{align}T_{\text {wind chill}}=T_{\text {air}}
\ for M \leq M_{o}\tag{3.64b}\end{align}\)
where a = 0.62, b = 0.51, T1 = 13.1°C, and T2 = 14.6°C. M is the wind speed measured at the official anemometer height of 10 m. For M < Mo, the wind chill equals the actual air temperature. This index applies to non-rainy air.
Figure 3.12 and Table 3-3 show that faster winds and colder temperatures make us “feel” colder. The data used to create eq. (3.64) was from volunteers in Canada who sat in refrigerated wind tunnels, wearing warm coats with only their face exposed.
| Table 3-3. The wind-chill-index temperature (°C). | |||||||
| Wind Speed | Actual Air Temperature (°C) | ||||||
| km· h-1 | m·s-1 | –40 | –30 | –20 | –10 | 0 | 10 |
| 60 | 16.7 | –64 | –50 | –36 | –23 | –9 | 5 |
| 50 | 13.9 | –63 | –49 | –35 | –22 | –8 | 6 |
| 40 | 11.0 | –61 | –48 | –34 | –21 | –7 | 6 |
| 30 | 8.3 | –58 | –46 | –33 | –20 | –6 | 7 |
| 20 | 5.6 | –56 | –43 | –31 | –18 | –5 | 8 |
| 10 | 2.8 | –51 | –39 | –27 | –15 | –3 | 9 |
| 0 | 0 | –40 | –30 | –20 | –10 | 0 | 10 |
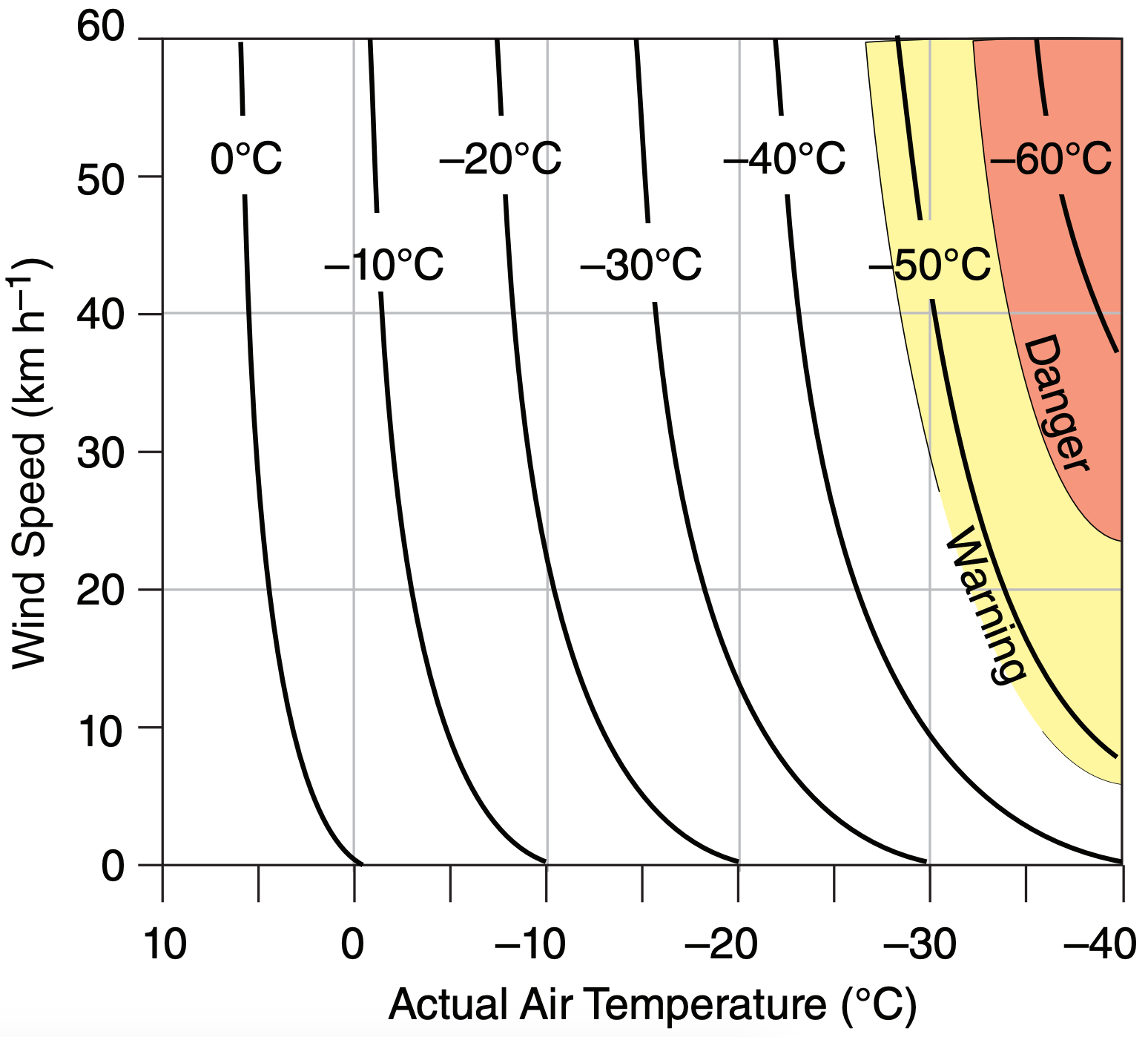
At wind chills colder than –27°C, exposed skin can freeze in 10 to 30 minutes. At wind chills colder than –48°C: WARNING, exposed skin freezes in 2 to 5 min. At wind chills colder than –55°C: DANGER, exposed skin freezes in less than 2 minutes. In this danger zone is an increased risk of frostbite (fingers, toes, ears and nose numb or white), and hypothermia (drop in core body temperature).
3.7.2. Humidex and Heat Index
On hot days you feel warmer than the actual air temperature when the air is more humid, but you feel cooler when the air is drier due to evaporation of your perspiration. In extremely humid cases the air is so uncomfortable that there is the danger of heat stress. Two apparent temperatures that indicate this are humidex and heat index.
The set of equations below approximates Steadman’s temperature-humidity index of sultriness (i.e., a heat index):
\(\ \begin{align}T_{\text {heat index}}\left(^{\circ} \mathrm{C}\right)=T_{R}+\left[T-T_{R}\right] \cdot\left(\frac{R H \cdot e_{s}}{100 \cdot e_{R}}\right)^{p}\tag{3.65a}\end{align}\)
where eR = 1.6 kPa is reference vapor pressure, and
\(\ \begin{align} T_{R}\left(^{\circ} \mathrm{C}\right)=0.8841 \cdot T+\left(0.19^{\circ} \mathrm{C}\right)\tag{3.65b}\end{align}\)
\(\ \begin{align}p=\left(0.0196^{\circ} \mathrm{C}^{-1}\right) \cdot T+0.9031\tag{3.65c}\end{align}\)
\(\ \begin{align}e_{s}(\mathrm{kPa})=0.611 \cdot \exp \left[5423\left(\frac{1}{273.15}-\frac{1}{(T+273.15)}\right)\right]\tag{3.65d}\end{align}\)
The two input variables are T (dry bulb temperature in °C), and RH (the relative humidity, ranging from 0 for dry air to 100 for saturated air). Also, TR (°C), and p are parameters, and es is the saturation vapor pressure, discussed in the Water Vapor chapter. Eqs. (3.65) assume that you are wearing a normal amount of clothing for warm weather, are in the shade or indoors, and a gentle breeze is blowing.
| Table 3-4. Heat-index apparent temperature (°C). | |||||||
| Rel. Hum. (%) |
Actual Air Temperature (°C) | ||||||
| 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
| 100 | 21 | 29 | 41 | 61 | |||
| 90 | 21 | 29 | 39 | 57 | |||
| 80 | 21 | 28 | 37 | 52 | |||
| 70 | 20 | 27 | 35 | 48 | |||
| 60 | 20 | 26 | 34 | 45 | 62 | ||
| 50 | 19 | 25 | 32 | 41 | 55 | ||
| 40 | 19 | 24 | 30 | 38 | 49 | 66 | |
| 30 | 19 | 24 | 29 | 36 | 44 | 56 | |
| 20 | 18 | 23 | 28 | 33 | 40 | 48 | 59 |
| 10 | 18 | 23 | 27 | 32 | 37 | 42 | 48 |
| 0 | 18 | 22 | 27 | 31 | 36 | 40 | 44 |
| Table 3-5. Humidex apparent temperature (°C) | |||||||
| Td (°C) |
Actual Air Temperature T (°C) | ||||||
| 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
| 50 | 118 | ||||||
| 45 | 96 | 101 | |||||
| 40 | 77 | 82 | 87 | ||||
| 35 | 62 | 67 | 72 | 77 | |||
| 30 | 49 | 54 | 59 | 64 | 69 | ||
| 25 | 37 | 42 | 47 | 52 | 57 | 62 | |
| 20 | 28 | 33 | 38 | 43 | 48 | 53 | 58 |
| 15 | 24 | 29 | 34 | 39 | 44 | 49 | 54 |
| 10 | 21 | 26 | 31 | 36 | 41 | 46 | 51 |
| 5 | 19 | 24 | 29 | 34 | 39 | 44 | 49 |
| 0 | 18 | 23 | 28 | 33 | 38 | 43 | 48 |
| –5 | 17 | 22 | 27 | 32 | 37 | 42 | 47 |
| –10 | 16 | 21 | 26 | 31 | 36 | 41 | 46 |
The dividing line between feeling warmer vs. feeling cooler is highlighted with the bold, underlined heat-index temperatures in Table 3-4.
In Canada, a humidex is defined as
\(\ \begin{align}T_{\text {humidex}}\left(^{\circ} C\right)=T\left(^{\circ} C\right)+a \cdot(e-b)\tag{3.66a}\end{align}\)
where T is air temperature, a = 5.555 (°C kPa–1), b = 1 kPa, and
\(\ \begin{align}e(\mathrm{kPa})=0.611 \cdot \exp \left[5418\left(\frac{1}{273.16}-\frac{1}{\left[T_{d}\left(^{\circ} \mathrm{C}\right)+273.16\right]}\right)\right]\tag{3.66b}\end{align}\)
Td is dew-point temperature, a humidity variable discussed in the Water Vapor chapter.
Humidex is also an indicator of summer discomfort due to heat and humidity (Table 3-3). Values above 40°C are uncomfortable, and values above 45°C are dangerous. Heat stroke is likely for humidex ≥ 54°C. This table also shows that for dry air (Td ≤ 5°C) the air feels cooler than the actual air temperature.
Sample Application
Use the equations to find the heat index and humidex for an air temperature of 38°C and a relative humidity of 75% (which corresponds to a dew-point temperature of about 33°C).
Find the Answer
Given: T = 38°C , RH = 75% , Td = 33°C
Find: Theat index = ? °C , Thumidex = ? °C
For heat index, use eqs. (3.65):
TR = 0.8841 · (38) + 0.19 = 33.8°C (3.65b)
p = 0.0196 · (38) + 0.9031 = 1.65 (3.65c)
es = 0.611·exp[5423·( {1/273.15} – {1/(38+273.15)})] = 6.9 kPa (3.65d)
Theat index = 33.8 + [38–33.8]·(0.75·6.9/1.6)1.65 = 62.9°C (3.65a)
For humidex, use eqs. (3.66):
e = 0.611·exp[5418·( {1/273.16} – {1/(33+273.16)})] = 5.18 kPa (3.66b)
Thumidex = 38 + 5.555·(5.18–1) = 61.2°C (3.66a)
Check: Units are reasonable. Values agree with extrapolation of Tables 3-4 and 3-5.
Exposition: These values are in the danger zone, meaning that people are likely to suffer heat stroke. The humidex and heat index values are nearly equal for this case.


