3.1: Ways to Specify Water Vapor
- Page ID
- 3362
Up to now, we have dealt with water vapor only as the specific humidity in order to determine the virtual temperature. But there are many ways for us to quantify the amount of water vapor in the atmosphere. The most common are specific humidity, water vapor mixing ratio, relative humidity, and dewpoint temperature.

Specific humidity (q) is the density of water vapor (mass per unit volume) divided by the density of all air, including the water vapor:
\[ \begin{align*} q &=\frac{m_{\text {water}_{-} \text {vapor}}}{m_{\text {all}_{-} \text {air}}} \\[4pt] &=\frac{\rho_{\text {water}_{-} \text {vapor}}}{\rho_{\text {all_air}}} \\[4pt] &=\frac{\rho_{v}}{\rho} \end{align*}\]
We have already seen that specific humidity is used to calculate virtual temperature. Specific humidity is unitless, but often we put it in g kg–1.
Water vapor mixing ratio (w) is the density of water vapor divided by the density of dry air without the water vapor:
\[ \begin{align*} w &=\frac{m_{\text {water}_{-} \text {vapor}}}{m_{d r y_{-} a i r}} \\[4pt] &=\frac{\rho_{\text {water}_{-}, \text {vapor}}}{\rho_{d v_{-}, \text {air}}} \\[4pt] &= \frac{\rho_{v}}{\rho_{d}} \end{align*}\]
Water vapor mixing ratio is widely used to calculate the amount of water vapor. It is also the quantity used on the skew-T diagram, which we will discuss later in this lesson. Water vapor mixing ratio is unitless, but often we put it in g kg–1.
Since
\[ρ_d = ρ – ρ)v\]
we can rearrange the equations to get the relationship between \(w\) (water vapor mixing ratio) and \(q\) (specific humidity):
\[q=\frac{w}{1+w}\]
\[w=\frac{q}{1-q}\]
The water vapor mixing ratio, w, is typically at most about 40 g kg–1 or 0.04 kg kg–1, so even for this much water vapor, q = 0.040/(1 + 0.040) = 0.038 or 38 g kg–1.
Thus, water vapor mixing ratio and specific humidity are the same to within a few percent. But specific humidity is less than the water vapor mixing ratio if the humidity is more than zero. Here is one example of global specific humidity.
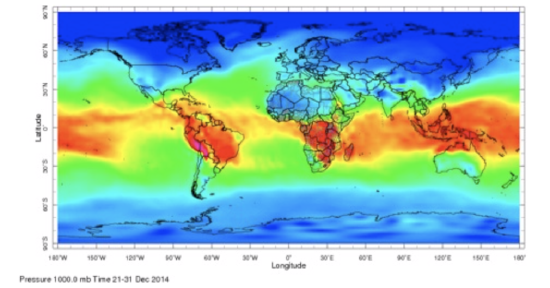
The greatest absolute specific humidity is in the tropics with maximum values approaching 30 g kg–1. The smallest values are at the high latitudes and are close to zero. Why is specific humidity distributed over the globe in this way?
Relative humidity (RH) is another measure of water vapor in the atmosphere, although we must be careful when using it because a low relative humidity may not mean a low water vapor mixing ratio (i.e., at high temperatures) and a high relative humidity might still be quite dry air (i.e., at low temperatures).
According to the World Meteorological Organization (WMO) definition,
\[R H=\frac{w}{w_{s}}\]
where ws is the saturation mixing ratio (the mixing ratio at which RH = 100%). w and ws can both have units of g kg–1 or kg kg–1, as long as they are consistent. Relative humidty is usually expressed as a percent. Thus, when w = ws, RH = 1 = 100%. In most problems involving RH, it is important to keep in mind conversions between decimal fractions and percent.
A more physically based definition of the relative amount of moisture in the air is the saturation ratio, S:
\[S=\frac{e}{e_{s}}\]
where e is the vapor pressure (hPa) and es is the saturation vapor pressure. The saturation ratio is used extensively in cloud physics (Lesson 5). To see how RH and S are related, start with the Ideal Gas Law and then do some algebra:
\[e=\rho_{v} R_{v} T\]
\[p_{d}=\rho_{d} R_{d} T\]
\[\varepsilon \equiv R_{d} /_{R}\]
so
\[w=\frac{\varepsilon e}{p_{d}}=\frac{\varepsilon e}{p-e}\]
\[\frac{w}{w_{s}}=\frac{e}{e_{s}}\left(\frac{p-e_{s}}{p-e}\right)\]
\[R H=S\left(\frac{p-e_{s}}{p-e}\right)\]
where ε = 0.622 is just the molar mass of water (18.02 kg mol–1) divided by the mass of dry air (28.97 kg mol–1). e and es are typically less than 7% of p, and since e is usually 20%–80% of es, the difference between the two definitions is usually less than a few percent.
Note that at saturation, you can replace w with ws and e with es in the equation that relates w to e.
Some processes depend upon the absolute amount of water vapor, which is given by the specific humidity, water vapor mixing ratio, and water vapor pressure, and other processes depend on the relative humidity. For example, the density of a moist air parcel depends on the absolute amount of water vapor. So does the absorption and emission of infrared atmospheric radiation. On the other hand, cloud formation depends on the relative humidity, although the cloud might be kind of wimpy if the absolute humidity is small.
One of the most common indicators of absolute humidity is the dewpoint temperature. We will postpone the discussion of it until after we learn about the relationship between temperature and saturation vapor pressure, es.
Exercise
If the density of water vapor is 10.0 g m–3 and the density of dry air is 1.10 kg m–3, what is the water vapor mixing ratio and what is the specific humidity?
- Click for answer
-
\(w=\frac{10.0 \mathrm{g} \mathrm{m}^{-3}}{1.10 \mathrm{kg} \mathrm{m}^{-3}}=9.09 \frac{\mathrm{g}}{\mathrm{kg}}\)
\(q=\frac{10.0 \mathrm{gm}^{-3}}{1.10 \mathrm{kg} \mathrm{m}^{-3}+\left(10.0 \mathrm{g} \mathrm{m}^{-3} / 1000 \mathrm{g} \mathrm{kg}^{-1}\right)}=9.01 \frac{\mathrm{g}}{\mathrm{kg}}\)
Exercise
If the water vapor mixing ratio is 21 g kg–1 and the relative humidity is 84%, what is the saturation water vapor mixing ratio?
- Click for answer
-
\(R H=\frac{w}{w_{s}} \quad \rightarrow \quad w_{s}=\frac{w}{R H}=\frac{21 \mathrm{g} \mathrm{kg}^{-1}}{0.84}=25 \mathrm{g} \mathrm{kg}^{-1}\)


