10.6: Equations of Motion in Spherical Coordinates
- Page ID
- 3414
The three variables used in spherical coordinates are:
- longitude (denoted by \(λ\))
- latitude (denoted by \(φ\))
- vertical distance (denoted by \(r\) from Earth’s center and by \(z\) from Earth’s surface, where \(z = r – a\) and \(a\) is Earth’s radius)
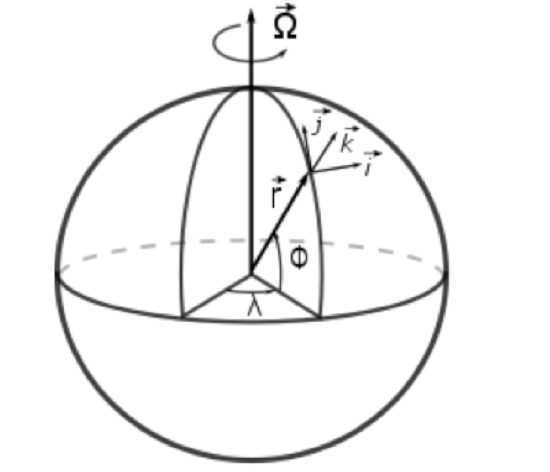
Note that the unit vectors in spherical coordinates change with position. For example, for an air parcel at the equator, the meridional unit vector, \(\vec{j}\), is parallel to the Earth’s rotation axis, whereas for an air parcel near one of the poles, \(\vec{j}\) is nearly perpendicular to the Earth’s rotation axis. In spherical coordinates, the velocity vector and its components are given by:
\[\vec{U}=u \vec{i}+v \vec{j}+w \vec{k}\]
\[u=r \cos \phi \frac{D \lambda}{D t}, \quad v=r \frac{D \phi}{D t}, \quad w=\frac{D z}{D t}\]
where u, v, and w are the eastward, northward, and upward components of the velocity, respectively. These velocities are derived from the changes in eastward, northward, and upward distances, which are given by:
\[d x=r \cos \phi d \lambda=\text { change in eastward distance } \cong a \cos \phi d \lambda\]
\[d y=r d \phi=\text { change in northward distance } \cong a d \phi\]
\[d z=d r=\text { change in upward distance }\]
Let’s now write the averaged momentum conservation equation [10.16] in component form in spherical coordinates. We will just show you how this conversion is done without actually taking you through all the steps. Note that we need to take the total derivatives of the unit vectors as well as the velocities:
\[\frac{D \vec{U}}{D t}=\frac{D}{D t}(\vec{i} u+\vec{j} v+\vec{k} w)=\vec{i} \frac{D u}{D t}+u \frac{D \vec{i}}{D t}+\vec{j} \frac{D v}{D t}+v \frac{\vec{D} \vec{j}}{D t}+\vec{k} \frac{D w}{D t}+w \frac{D \vec{k}}{D t}\]
The terms containing derivatives of the unit vectors are called “metric terms.” They depend on the Earth being a sphere. In Cartesian coordinates, they equal zero.
Consider just one of these metric terms:
\[\frac{\vec{D} \vec{j}}{D t}=\frac{\partial \vec{j}}{\partial t}+u \frac{\partial \vec{j}}{\partial x}+v \frac{\partial \vec{j}}{\partial y}+w \frac{\partial \vec{j}}{\partial z}=0+u \frac{\partial \vec{j}}{\partial x}+v \frac{\partial \vec{j}}{\partial y}+0\]
Since for any location, \(\vec{j}\) is constant with time and \(\vec{j}\) does not change as a function of altitude, that leaves \(\vec{j}\) dependent only on latitude and longitude. Look at \(\frac{\partial \vec{j}}{\partial y}\) first. Set y = 0 at the equator, and y = a (Earth’s radius) near the pole. As noted above, at the equator, \(\vec{j}\) is parallel to Earth’s rotation axis, but near the pole, it is almost perpendicular to it. Thus the change in \(\vec{j}\) going from south to north (increasing y) must be pointing down to Earth’s center and so \(\vec{j}\) changes by −\(\vec{k}\) times a small angular change while y changes by a times the same small angular change. The net result is that:
\[\frac{\partial \vec{j}}{\partial y}=\frac{-\vec{k}}{a}\]
Using the same approach, we can show that:
\[\frac{\partial \vec{j}}{\partial x}=\frac{-\tan \phi}{a} \vec{i}\]
The total derivatives of all three unit vectors are:
\[\frac{\vec{D} \vec{i}}{D t}=\frac{u}{a \cos \phi}(\vec{j} \sin \phi-\vec{k} \cos \phi)\]
\[\frac{\vec{D} \vec{j}}{D t}=-\frac{u \tan \phi}{a} \vec{i}-\frac{v}{a} \vec{k}\]
\[\frac{\vec{D} \vec{k}}{D t}=\frac{u}{a} \vec{i}+\frac{v}{a} \vec{j}\]
Putting this all together:
\[\begin{aligned} \frac{D \vec{U}}{D t}=&\left(\frac{D u}{D t}-\frac{u v \tan \phi}{a}+\frac{u w}{a}\right) \vec{i}+\\ &\left(\frac{D v}{D t}+\frac{u^{2} \tan \phi}{a}+\frac{u w}{a}\right) \vec{j}+\\ &\left(\frac{D w}{D t}-\frac{u^{2}+v^{2}}{a}\right) \vec{k} \end{aligned}\]
Similar analysis can be done for the other terms in the averaged momentum equation.
Coriolis force:
\[-2 \vec{\Omega} \times \vec{U}=2 \Omega(v \sin \phi-w \cos \phi) \vec{i}-(2 \Omega u \sin \phi) \vec{j}+(2 \Omega u \cos \phi) \vec{k}\]
Gravity:
\[\vec{g}=-g \vec{k}\]
Pressure Gradient Force (PGF):
\[-\frac{1}{\rho} \vec{\nabla} p=-\frac{1}{\rho} \frac{\partial p}{\partial x} \vec{i}-\frac{1}{\rho} \frac{\partial p}{\partial y} \vec{j}-\frac{1}{\rho} \frac{\partial p}{\partial z} \vec{k}\]
Turbulent friction (in the boundary layer only):
\[-\frac{C_{d}}{h}|\vec{V}| \vec{V}=-\frac{C_{d}}{h}|\vec{V}| u\left|u \vec{i}-\frac{C_{d}}{h}\right| \vec{V}|v| \vec{v} \vec{j}\]
Adding together all of the forces, the averaged momentum equations in spherical coordinates in the zonal, meridional, and vertical directions are, respectively:
\[\frac{D u}{D t}-\frac{u v \tan \phi}{a}+\frac{u w}{a}=-\frac{1}{\rho} \frac{\partial p}{\partial x}+2 \Omega v \sin \phi-2 \Omega w \cos \phi-\frac{C_{d}}{h}|\vec{V}| u\]
\[\frac{D v}{D t}-\frac{u^{2} \tan \phi}{a}+\frac{v w}{a}=-\frac{1}{\rho} \frac{\partial p}{\partial y}-2 \Omega u \sin \phi-\frac{C_{d}}{h}|\vec{V}| v\]
\[\frac{D w}{D t}-\frac{u^{2}+v^{2}}{a}=-\frac{1}{\rho} \frac{\partial p}{\partial z}-g+2 \Omega u \cos \phi\]


