10.5: Effects of Earth’s Rotation- Apparent Forces
- Page ID
- 3413
Newton’s Laws apply in an inertial reference frame, that is, one that is not accelerating. A point on the rotating Earth is not following a straight line through space, but instead is constantly accelerating by rotating away from a straight line. Therefore, Earth does not provide an inertial reference frame. From the point of view of an astronaut in distant space, the air motions she would observe obey Newton’s Law perfectly, but from the point of view of an Earth-bound observer, Newton’s Laws fail to capture the observed motion. To account for this crazy behavior, the Earth-bound observer needs to add some apparent forces to the real forces for the math to explain the observed motion from the point of view of someone standing on the rotating Earth.
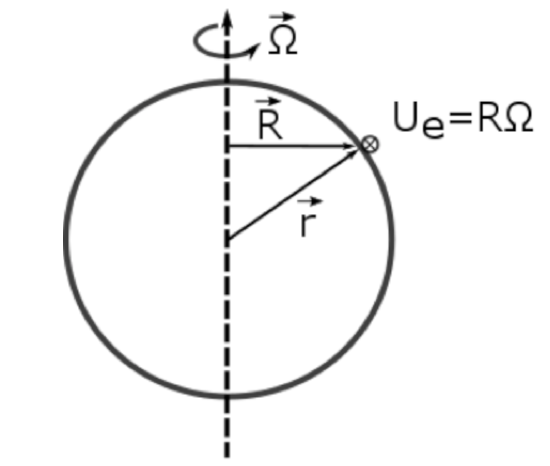
Suppose we have an air parcel moving through space with a velocity \(\vec{U}_{a}\), which we will call the absolute velocity. We want to relate this absolute velocity to \(\vec{U}\), the velocity observed with respect to the Earth reference frame. Let \(\vec{U}_{e}\) be the velocity of the Earth. Here we only consider the velocity of the Earth due to rotation about its axis (the motion around the Sun is much less important), so \(\vec{U}_{e}\) is always eastward, greatest at the equator and zero at the poles. The absolute velocity of an air parcel is simply the velocity of the air parcel with respect to the Earth plus the velocity of the Earth itself: \(\vec{U}_{a}=\vec{U}+\vec{U}_{e}\)
What is the velocity of the Earth? Consider a specific point on the Earth. Let \(\vec{\Omega}\) be Earth’s angular velocity vector, \(\vec{r}\) be the position vector from the Earth’s center to the point in question, and \(\vec{R}\) be the shortest distance vector from the axis of rotation to the point in question (as in the figure above). The magnitude of \(\vec{\Omega} \text { is }|\vec{\Omega}|=\frac{2 \pi}{23.934 \mathrm{hr}} \frac{1 \mathrm{hr}}{3600 \mathrm{s}}=7.292 \times 10^{-5} \mathrm{s}^{-1}\) and the direction of \(\vec{\Omega}\) is determined by the right hand rule (the direction of your thumb when you curl the fingers of your right hand in the direction of rotation and point your thumb towards the North Star). To determine the angular velocity of the Earth, note that we have used the sidereal day length, 23.934 hr, which is the day length when Earth's rotation is measured with respect to the fixed stars (the inertial reference frame).
The following video (:51) will demonstrate the right hand rule:
UE Right Hand Rule
- Click here for transcript of the UE Right Hand Rule video.
-
u sub e is the eastward velocity of the Earth. It is pointed into the page. We know the u sub e equals r-- which is the shortest distance vector between Earth's rotation axis and the point on the surface-- times omega, which is Earth's rotation vector. The units of omega are seconds to the minus 1, which makes it a frequency. Note that u sub e equals r times omega, which is also equal to omega cross r. We can see this if you take your right hand with your fingers pointed in the omega direction and the palm in the r direction. And you fold your fingers into the palm. Your thumb will point into the page, which is the direction of u sub e and is in the positive x direction.
The magnitude of \(\vec{U}_{e}\) is \(R \Omega,\) but we need to write \(\vec{U}_{e}\) as a vector. Note that \(\vec{U}_{e}\) is pointed into the page in the figure above, which is a direction perpendicular to both \(\vec{\Omega}\) and \(\vec{R}\). Hence we can use the cross product equation to write an expression for Earth's velocity: \(\vec{U}_{e}=\vec{\Omega} \times \vec{R}=\vec{\Omega} \times \vec{r}\), since the component of \(\vec{r}\) perpendicular to \(\vec{\Omega}\) is \(\vec{R} .\) So:
\[\vec{U}_{a}=\vec{U}+\vec{\Omega} \times \vec{r}\]
We have thus related velocity in the absolute reference frame to velocity in the rotating reference frame.
Now we can consider acceleration. Since \(\vec{U}=\frac{D \vec{r}}{D t} \text { and } \vec{U}_{a}=\frac{D_{a} \vec{r}}{D t}\) we can write:
\(\frac{D_{a} \vec{r}}{D t}=\frac{D \vec{r}}{D t}+\vec{\Omega} \times \vec{r}\)
This equation describes the change in a position of an air parcel with time observed from an inertial reference frame (the derivative on the left) to the change with time observed from Earth’s reference frame (the derivative on the right). Equation [10.11] is general and applies not only to \(\vec{r}\) but also to any other vector.
Let’s replace \(\vec{r}\) on the left hand side with \(\vec{U}_{a}\) and \(\vec{r}\) on the right hand side with \(\vec{U}+\vec{\Omega} \times \vec{r}\) since these two expressions equal each other in Equation [10.10]. By making these substitutions, we can relate acceleration in the absolute frame to acceleration in the rotating frame:
\[\frac{D_{a} \vec{U}_{a}}{D t}=\frac{D \vec{U}}{D t}+\frac{\vec{D} \vec{\Omega}}{D t} \times \vec{r}+\vec{\Omega} \times \frac{D \vec{r}}{D t}+\vec{\Omega} \times \vec{U}+\vec{\Omega} \times(\vec{\Omega} \times \vec{r})\]
We can simplify this equation and then we can make sense of it physically. First, \(\vec{\Omega}\) is not changing significantly with time, so \(\frac{D \vec{\Omega}}{D t}\) can be set to zero. Second, \((\vec{\Omega} \times \vec{r})\) has the magnitude of ΩR and points to the east (by the right hand rule) and thus \(\vec{\Omega} \times(\vec{\Omega} \times \vec{r})\) has the magnitude \(\Omega^{2} R\) and points toward – \(\vec{R}\). Finally, noting that \(\vec{U}=\frac{D \vec{r}}{D t}\), we end up with the equation:
\[\frac{D_{a} \vec{U}_{a}}{D t}=\frac{D \vec{U}}{D t}+2 \vec{\Omega} \times \vec{U}-\Omega^{2} \vec{R}\]
The term on the left is the acceleration in the absolute inertial reference frame. The first term on the right is the acceleration in the Earth reference frame. The remaining terms are the apparent accelerations. The first one is the Coriolis acceleration and the second one is the centripetal acceleration.
We can now combine Equation [10.13] with the version of Equation [10.9] that is averaged to get:
\[-\frac{1}{\rho} \vec{\nabla} p+\vec{g} *-\frac{C_{d}}{h}|\vec{V}| \vec{V}=\frac{D \vec{U}}{D t}+2 \vec{\Omega} \times \vec{U}-\Omega^{2} \vec{R}\]
and then rearrange this equation to get:
\[\frac{D \vec{U}}{D t}=-\frac{1}{\rho} \vec{\nabla} p+\vec{g} *-\frac{C_{d}}{h}|\vec{V}| \vec{V}-2 \vec{\Omega} \times \vec{U}+\Omega^{2} \vec{R}\]
The first three terms on the right hand side of Equation [10.14] are the real forces. The fourth and fifth terms on the right hand side are the apparent forces: the Coriolis force and the centrifugal force, respectively.
Centrifugal Force
The centrifugal force is directed away from the Earth's axis of rotation and is the same type of force that you feel when you are in a car going around a sharp curve. Over its long history, all the material that makes up the Earth has adjusted to the real gravitational force, \vec{g}^{*}, which is directed to Earth’s center, and the apparent centrifugal force that is directed away from Earth’s rotation axis (see figure below).
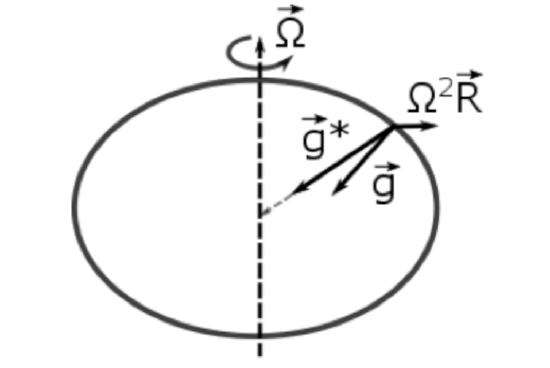
The gravity we feel is the sum of gravity pointed toward Earth’s center and the outward centrifugal force. The effect is greatly exaggerated to show the vectors. The gravity we feel, \(\vec{g}\) , is perpendicular to Earth's flat surfaces at rest (i.e., oceans). Credit: W. Brune
The resulting gravity that the Earth and everything on it feels is the vector sum of this real and this apparent force:
\[\vec{g}=\overrightarrow{g^{*}}+\Omega^{2} \vec{R}\]
Since the centrifugal force depends on \(\vec{R}\), it is greatest at the equator and zero at the poles. As a result of the centrifugal force, the Earth has become slightly oblate, with an equatorial radius of 6378.1 km that is 0.34% greater than the polar radius of 6356.8 km. Note that \(\overrightarrow{\boldsymbol{g}}\) is always perpendicular to Earth’s surface, which is very useful because the vertical coordinate is always chosen to be perpendicular to Earth's surface, so that \(\overrightarrow{\boldsymbol{g}}\) is only in the z direction and, as the figure above indicates, does not point towards the center of the Earth (except at the poles and the equator). The value of g at the equator is \(9.780 \mathrm{ms}^{-2},\) which is 0.052\(m s^{-2}\) smaller than the value of g at the poles, which is 9.832 m s–2. The centrifugal force at the equator is \(\Omega^{2} R=\left(7.27 \times 10^{-5} \mathrm{s}^{-1}\right)^{2}\left(6.378 \times 10^{6} \mathrm{m}\right)=0.033 \mathrm{m} \mathrm{s}^{-2}\), and hence accounts for more almost 2/3 of the difference in g between the equator and the poles. The rest of the difference is due to the difference in g*, which is overestimated by the difference in equatorial and polar radii--the problem is more complicated than it might appear because Newton's law of gravitation only applies to point masses. At any rate, the difference between g at the poles and equator is small enough for a constant value of g = 9.8 m s–2 to be suitable for most applications in atmospheric dynamics.
Combining Equations [10.14] and [10.15] yields a more useful form of the averaged momentum conservation in the rotating reference frame:
\[\frac{\overrightarrow{D U}}{D t}=-\frac{1}{\rho} \vec{\nabla}_{p}+\vec{g}-\frac{C_{d}}{h}|\vec{V}| \vec{V}-2 \vec{\Omega} \times \vec{U}\]
We will now move on to a discussion of the Coriolis Force. The following video (3:05) gives a basic introduction.
Coriolis Effect
- Click here for transcript of the Coriolis Effect video.
-
[MUSIC PLAYING]
If you've ever watched the news during a hurricane or wintertime Nor'easters, you've probably noticed that big storms spin over time as they travel. In the northern hemisphere, they spin counterclockwise. But if you were watching a storm in the southern hemisphere, you'd see it spinning clockwise.
Why do storms spin in different directions depending on their location, and why do they spin in the first place? A storm's rotation is due to something called the Coriolis effect, which is a phenomenon that causes fluids like water and air to curve as they travel across or above Earth's surface.
Here's the basic idea-- Earth is constantly spinning around its axis from west to east, but because Earth is a sphere and wider in the middle, points on the equator are actually spinning faster around the axis than points near the poles. So imagine you were standing in Texas and had a magic paper airplane that could travel hundreds of miles. If you threw your airplane directly northward, you might think it would land straight north-- maybe somewhere in Nebraska.
But Texas is actually spinning around Earth's axis faster than Nebraska is because it's closer to the equator. That means that the paper airplane is spinning faster as well. And when you throw it, that spinning momentum is conserved. So if you threw your paper airplane in a straight line toward the north, it would land somewhere to the right of Nebraska-- maybe in Delaware.
So from your point of view in Texas, the plane would have taken a curved path to the right. The opposite would happen in the southern hemisphere. An object traveling from the equator to the south would get deflected to the left.
So what does this have to do with hurricanes spinning? Well, at the center of every hurricane is an area of very low pressure. As a result, the high-pressure air surrounding the center, or eye of a storm, is constantly rushing toward the low-pressure void in the middle. But because of the Coriolis effect, the air rushing toward the center is deflected off course.
In the northern hemisphere, the volumes of air on all sides of the eye keep getting tugged slightly to the right. The air keeps trying to make its way to the middle, and keeps getting deflected, causing the entire system to spin in a counterclockwise direction. In the southern hemisphere, where the Coriolis effect pulls air to the left, the opposite happens. Storms spin around the eye in a clockwise manner.
Credit: NOVA PBS
Coriolis Force
The Coriolis force, \(-2 \vec{\Omega} \times \vec{U}\), acts on an air parcel (or any other object) only when it is moving with respect to the Earth. It acts perpendicular to Earth's angular velocity vector and the air parcel's velocity vector. The explanation for the Coriolis force is usually broken into an explanation in the zonal (constant latitude) direction and the meridional (constant longitude) direction.
Zonal Flow (East–West Wind Velocity)
Consider an air parcel that is initially at rest and in hydrostatic balance but is impulsively accelerated to a velocity u to the east (see left side of figure below). Initially when it was at rest, it had the same acceleration as the Earth below it. However, after it accelerated to velocity u, it suddenly had more acceleration than it had before, throwing it out of hydrostatic balance. Look at the change in acceleration that comes from the air parcel suddenly acquiring a velocity to the east, which is just the acceleration after the velocity changes minus the acceleration before the velocity changes and equals \((\Omega+u / R)^{2} R-\Omega^{2} R\). To a very good approximation, this change equals the Coriolis force, \(2 \Omega u\).
There is a vertical component that points up, but there is also a horizontal component of force that points to the right of the motion in the Northern Hemisphere and to the left in the Southern Hemisphere.
Now consider an air parcel that is initially at rest but is impulsively accelerated to a velocity u to the west (see right side of figure below). The air parcel suddenly has less angular momentum than it had before and experiences a decreased centrifugal force. This decrease in angular momentum, to a very good approximation, equals the Coriolis force, \(2 \Omega u\), but is pointed toward Earth's axis of rotation. There is a vertical component that points down, but the horizontal component of force that points to the right of the motion in the Northern Hemisphere and to the left in the Southern Hemisphere.
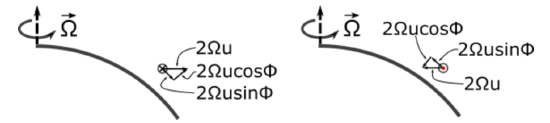
We can write down the accelerations in the y and z directions due to the air moving to the east with speed u:
Coriolis acceleration in the y direction= \(\frac{D v}{D t}=-2 \Omega u \sin \phi\)
Coriolis acceleration in the z direction= \(\frac{D w}{D t}=2 \Omega u \cos \phi\)
Meridional Flow (North–South Velocity)
What about an air parcel traveling to the north at a constant altitude? Note that the air parcel moving north starts at a greater distance from Earth’s axis and comes closer to Earth’s axis if it moves at the same height above the surface. Its angular momentum is conserved, so it is moving faster to the east than the Earth beneath it. As a result, it appears to move to the right or the east.
If the same air parcel moves to the south at the same height above Earth’s surface, then it moves to a greater distance from Earth’s rotation axis. Its angular momentum becomes less than that of Earth, it slows down relative to Earth, and it veers to the right of south or to the west.
In both the zonal and meridional flow cases, the air parcel's velocity with respect to the Earth causes the air parcel to have a different angular momentum from the Earth below it. Conservation of angular momentum during that motion requires that the apparent Coriolis force be added in order to describe the observed motion. See the video below (2:11) for further explanation:
Coriolis Explanation
- Click here for transcript of the Coriolis Explanation video.
-
Coriolis force is an apparent force that accounts for motion on a rotating sphere, such as Earth. We can break the explanation of the Coriolis force in two cases-- zonal flow, which is east west, and Meridional flow, which is north south. The explanation for both cases relies on conservation of angular momentum. For zonal flow, imagine an air parcel moving to the east with velocity, u. Angular acceleration is just the angular velocity squared times the radius of rotation. If the parcel is moving at a velocity of u relative to Earth's surface, then it has some extra angular momentum, which is u divided by r. To find the total angular acceleration that the moving air parcel has, we need to square the angular momentum of the air parcel, which is omega plus u divided by r, and then multiply it by r. We then subtract the Earth's acceleration, which is just omega squared r. The difference, to good approximation, is 2 omega times u, which is just the Coriolis force, and, in the case of eastward motion, is pointed away from Earth's axis in the northern hemisphere. Thus, the Coriolis force turns the air parcel to the right for zonal flow. If the air parcel moves to the west, then by the same argument the Coriolis force points towards Earth's rotation axis in the northern hemisphere, which again turns the air parcel to the right. The explanation for the Meridional flow is simpler. An air parcel initially has the angular momentum of the Earth at its latitude. If it moves north at the same height, then it has more angular momentum than the Earth below it. And so it goes faster than the Earth and appears to move to the right. If it moves south at the height, then it has less angular momentum than Earth and appears to slow down relative to Earth and thus appears to move to the right.
Finding the Magnitude and Direction of the Coriolis Force
The magnitude of the horizontal Coriolis force is simply \(2 \Omega|\vec{V}| \sin \varphi\), where \(\varphi\) is the latitude. This magnitude applies to both the Northern and Southern Hemispheres. The direction of the Coriolis force is 90 degrees to the right of the horizontal velocity vector in the Northern Hemisphere and 90 degrees to the left of the horizontal velocity vector in the Southern Hemisphere.


