4.5: Earthquake Population Statistics and Recurrence Intervals
- Page ID
- 7008
How many earthquakes?
Here is an important observation about earthquake populations worldwide: earthquakes of a given magnitude happen about 10 times as frequently as those one magnitude unit larger.
Worldwide Frequency of Occurrence of Earthquakes
| Magnitude | Average Annually | How we know |
| 8 and higher | 1 | observations since 1900 |
| 7.0-7.9 | 15 | observations since 1900 |
| 6.0-6.9 | 134 | observations since 1990 |
| 5.0-5.9 | 1319 | observations since 1990 |
| 4.0-4.9 | 13,000 | estimated |
| 3.0-3.9 | 130,000 | estimated |
| 2.0-2.9 | 1,300,000 | estimated |
Annual earthquake population statistics compiled by the USGS.
Video: Earthquake Frequency-Magnitude Relationships Introduced (3:41)
Earthquake Frequency-Magnitude Relationships Introduced
- Click here for the transcript of Earthquake Frequency-Magnitude Relationships Introduced.
-
PRESENTER: This data table comes from the USGS and it tells you how many earthquakes of a given magnitude happen on average every year all over the world. So you can see that there are way fewer really big earthquakes than small earthquakes, and that's a good thing.
I like to make a plot out of this data because I think it's more instructive to make a plot. So over here, I've already drawn my axes. This is magnitude on the x-axis, and this is number of earthquakes on the y-axis. And you can see that I've made a log scale plot here. So this is 10, this is 100 million up here.
Why don't we just plot this data from this table onto this and we'll see what it looks like? So how many earthquakes of eight and higher are there? Well, there's about one, and that is right about here on my plot. For magnitude seven, it's about 15. That's about here. For magnitude sixes, 134, that's about here. And fives, a little bit over 1,000. Magnitude fours, a little bit over 10,000. Magnitude threes, estimated to be a little over 130,000. Magnitude twos, estimated to be a little over a million.
Magnitude ones and anything smaller aren't in this table. But I bet we can just extrapolate it, can't we? Because if we connect up all these points, we have drawn a line. So I can extrapolate that magnitude ones are probably a little over 10 million, and magnitude zeros, anything smaller, is a little over a hundred million. Magnitude is a log scale, so it actually is meaningful to have a magnitude zero.
All right, so we've drawn this line. And when I was a kid in school, I learned that the formula for a line is y equals mx plus b. So why don't we write this formula in terms of what we know about this plot, all right? What's y? Well, y is the number of earthquakes as a log scale, right? So it's actually log of the number.
Slope. Slope is rise over run, right? So the rise is actually negative minus one unit on our plot, and the run is plus one unit on our plot. So that's a slope of negative 1. And x is magnitude. And the y-intercept is a little over 100 million. It's probably 130 million, right? That's how the numbers are going up. So we could just guess 130 million.
So the log-- log of the number of earthquakes equals negative 1 times the magnitude plus 130 million for the whole world for a year. Now who cares, right? Why why are we bothering to write this down? Well, the reason is that, in fact, you will verify in your problem set that this slope is always negative one. No matter what part of the world it is and no matter what the timescale is. The only thing that changes when you don't look at the whole world annually is that this y-intercept will change, right? Because if you look at, say, California, there's fewer earthquakes in California than the whole world, right?
But this line is basically always true. So if you want to predict how often a really big earthquake is going to happen, then it's important to keep track of how many small ones happen because then you can draw this line and guess how often the big ones happen. That's what you're going to do in your problems set.Credit: Dutton
Earthquake populations approximately follow this relationship
\log N=a-b M
This is a power-law equation in which N is the number of earthquakes whose magnitude exceeds M and a and b are constants. For the majority of earthquake catalogs, the constant b is approximately equal to 1. When b≈ 1, this equation describes a line whose slope is about -1.
Seismologists can test the validity of the equation above using catalogs of earthquakes to make "frequency-magnitude diagrams." These diagrams show how many earthquakes of a given magnitude there are in a population of earthquakes.
A frequency-magnitude plot with real data! You can also read a transcript of my discussion of a frequency-magnitude diagram of a year's worth of earthquakes from around the world.
Now observe the plot below. For two separate catalogs of earthquakes that occurred in the New Madrid region, magnitude is plotted vs. the mean annual occurrence of earthquakes greater than or equal to a given magnitude. This plot is only different from the example plot above in that the N values on the y-axis have been normalized to one year. This is so two catalogs that span different lengths of time can be compared directly.
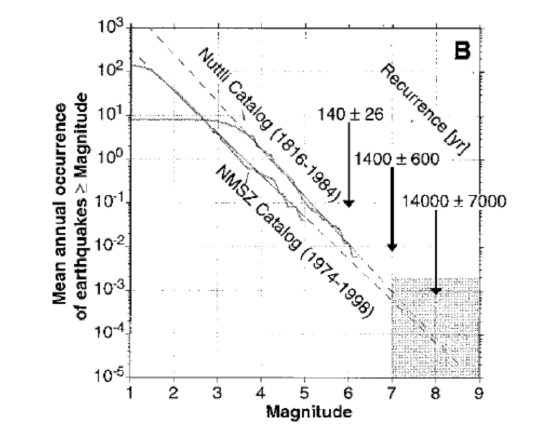
Credit: Newman et al., 1999.
Video: Earthquake frequency-magnitude data for the NMSZ Explained (3:32)
Earthquake frequency-magnitude data for the NMSZ Explained
- Click here for the transcript of Earthquake frequency-magnitude data for the NMSZ Explained.
-
PRESENTER: What do I see when I look at this plot? I see that we have magnitude on the x-axis and we have mean annual occurrence of earthquakes greater than or equal to some magnitude on the y-axis. So this means this plot is the same as the plot that we sketched earlier, showing how often earthquakes of different magnitudes happen.
But this data is not for the whole world. It's just for the New Madrid seismic zone. And there's two different data sets being plotted on top of each other here. So let's just look at those.
One is Otto Nuttli's catalog. And it spans 1816 through 1984. It might be a little hard to see, so I'll just draw over it. But it looks like this. It goes down here and there's some kind of jaggedy curves like that.
OK. The other catalog is the New Madrid Seismic Zone catalog. This is the digital catalog. And it's shorter. It only spans 24 years. It looks sort of like this.
Great. So the difference between these two catalogs is that one spans a lot longer in time. But since it isn't a digital catalog, it doesn't have as many small earthquakes in it. The other one has more small earthquakes, but isn't as long in time, so it doesn't have as many big earthquakes.
And neither of these looks exactly like the plot we sketched. Remember the plot we sketched looks sort of like this. We had magnitude here and log of the number here. And there was this perfect straight line.
And these don't have that perfect straight line. They tip over and kind of go flat at some point. But you can extrapolate if they did have a perfect straight line it would look like this.
So what this is saying is that earthquakes smaller than about magnitude 3 in the Nuttli catalog, or about magnitude 1 and 1/2 or so in the digital catalog, those earthquakes are there, but they're just not getting recorded. So when a plot like this flatlines, that's what it means.
At this end, it's not a pretty straight line. It's kind of jaggedy. That's just because the catalog is limited in time, so there's just not enough big earthquakes to really do useful statistics.
In order to get a recurrence interval, these researchers extrapolate from the part where they have data to the part where they don't. And they calculate these time intervals.
This is how often you can expect a magnitude 6 to happen in this region based on this earthquake data. Here's how often you can expect a magnitude 7. And here's how often you can expect a magnitude 8.
Now is a good time to point out that uncertainty in the magnitude of those historic earthquakes in 1811 and 1812 becomes uncertainty in calculating the recurrence interval, because it makes a big difference if you know you're trying to calculate how often a magnitude 7 is going to happen as opposed to how often a magnitude 8's going to happen, right? See how different these numbers are.
So there's kind of two big ways that you can have uncertainty in one of these calculations. One is just the limit of your catalog. The shorter your catalog is in time, the more you have to extrapolate from what you know to what you don't know. And the more uncertainty you have in the magnitude of the earthquake that you're looking for, like whether it's a 8 or an 8, the more uncertain you're going to be in calculating a recurrence time also.Credit: Dutton
Both of the curves in the plot above deviate from a straight line relationship log N = a - bM at small magnitudes. For the Nuttli Catalog, the line has a slope of about -1 at magnitudes greater than 3.5 and for the NMSZ catalog, the line has a slope of about -1 for approximately magnitude 1.5 and greater. Doesn't it look like in the Nuttli Catalog, there is the same number of magnitude 2 earthquakes every year as there are magnitude 3 earthquakes? But didn't we say that there should be ten times more magnitude 2's? What's going on?
Furthermore, how come there aren't any big earthquakes in this plot? The New Madrid Seismic Zone (NMSZ) catalog peters out at about magnitude 5 and the Nuttli Catalog doesn't have anything much over magnitude 6. But we know there have been big earthquakes in this region in the past, (or else why argue about seismic risk here), so where are they?
Limits of our observations
The answer to both of these problems is simply that any catalog of earthquakes is limited in two ways (pencast graphical explanation of observation limits). The first way is that not every piece of the Earth has a seismometer sitting on it, therefore there will be some small earthquakes that don't get recorded, even though they happened. For most catalogs, some standard is applied with regard to how many seismometers have to record an earthquake in order to include it in the catalog. This is for quality control reasons. It is hard to locate an earthquake and calculate its origin time within acceptable error limits if not enough stations recorded it. Therefore, the farther apart the seismometers are, the fewer small earthquakes will end up being included in the catalog. For the Nuttli Catalog, we can say that the catalog is incomplete below the threshold of M ≈ 3.5 because that is where the slope of the line (or the "b-value") begins to deviate from -1. The threshold for the NMSZ catalog is lower. Why do you think this is?
The second way a catalog is limited is that it is finite in time. Let's say for a given region, magnitude 8 earthquakes happen once every 1,000 years or so. If your catalog only spans 10 years, how likely are you to have a magnitude 8 in your catalog? For that matter, how likely are you to have a magnitude 7 in your catalog? How many magnitude 6's can you expect in 10 years? In the plot above, the time ranges for both catalogs are listed on the plot. Why does the NMSZ catalog have a lower maximum magnitude than the Nuttli Catalog?
Calculating a recurrence interval from a seismic catalog
In order to assess seismic risk, we want to know how often a large earthquake happens in this region. How do we do that if our seismometers haven't ever recorded a big earthquake? We have to extrapolate using the data that we do have. Extrapolation is a tricky business because small uncertainties turn into huge uncertainties the farther away you get from what you've actually measured. For a catalog of seismicity, we rely on the assumption that the relationship log N = a - bM holds true overall magnitudes and times. We then extend our catalog data into the realm of the unknown and predict how often large magnitude earthquakes are expected. In the plot above from Newman et al., 1999, they use dashed lines to show their extrapolations. How often do they predict a magnitude 7 will happen in the NMSZ? What about a magnitude 8? What uncertainties do they associate with these predictions?
How to extrapolate seismic catalog data in order to calculate a recurrence interval! You can also read a transcript of my explanation of extrapolating catalog data to calculate a recurrence interval.


